初识密码学

摩斯密码

加密之前先来认识一下摩尔斯电码

点划	图像	二叉树

SOS并不是任何求救英文的缩写，而是因为在摩尔斯电码中，S为. . .，O为_ _ _，所以SOS对于发报方是最容易发出的信号，对于接收方是最容易识别的信号，因此国际无线电报公约组织于1908年正式将它确定为国际通用海难求救信号。

在那些不懂摩尔斯电码的人眼中，将字母或数字转换成摩尔斯电码，就成了摩斯密码。因为摩尔斯电码是二状态符，如果只是简单的交流信息，也可以用0和1来代表点和划。

示例：
\qquad 明文：LOVE    密文：$\cdot -\cdot \cdot /---/\cdots -/\cdot (或0100\ast 111\ast 0001\ast 0)$
\qquad 明文：1314      密文：$\cdot ----/\cdots --/\cdot ----/\cdot \cdot \cdot \cdot -(或01111\ast 00011\ast 01111\ast 00001)$

猪圈密码

自己感觉挺意思的。就是将字母替换为另一种有序符号，直接看图吧

下图可以用于记忆	下图是每个字母对应的符号（对比左图就知道怎么回事了）

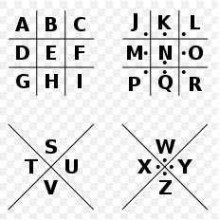示例：

键盘密码

只要是利用键盘来加密的，都可以叫做键盘密码。我大体上了解三种

普通键盘密码

来源	替换方法（对比左图就知道怎么回事了）

此加密方法就是字母换字母，右图展示的或许是标准的加密方法（具体标准的啥样没搜到），右图是将左图的红体当明文，黑体当密文。
不同的替换方式加密结果自然也不同。
示例：
\qquad 明文：LOVE    密文：SIWC(黑色–>红色) 或 SGCT(红色–>黑色)

用键盘换数字

列号加行号组成的一个两位数对应一个字母。如果反过来行号加列号貌似也没什么问题。
示例：
\qquad 明文：LOVE    密文：92914331(正常读法) 或 29193413(行加列)

要是把行号变成321的顺序，又会是不同的结果。不过类似于这样的替换加密，没必要纠结太多

拼音九键

这个就没有歧义了。字母替换成一个两位的数字。拼音九键将字母分在了八个小块中，每块里有三个或四个。
示例：L 数字5中的第3个；O 数字6中的第3个；V 数字8中的第3个；E 数字3中的第2个；
\qquad 明文：LOVE    密文：53638332

栅栏密码

把要加密的明文分成N个一组，然后把每组的第1个字连起来，形成一段无规律的话。一般N取两行。这种加密方法对于中国话来说用处不大，汉语顺序乱了也能看出大概意思。
示例：

• 明文：SHANYOUMUXIMUYOUZHI
• 密文：SIHMAUNYOOUUZMHUIX

加密过程：
（1）将字母写成两行$\begin{array}{c}SHANYOUMUX\\ IMUYOUZHI\end{array}$
（2）从上往下重新读一遍就是加密结果 ： SIHMAUNYOOUUZMHUIX

另一直玩法是竖着写$\begin{array}{c}SAYUUIUOZI\\ HNOMXMYUH\end{array}$，横这读 ： SAYUUIUOZI HNOMXMYUH

恺撒密码

这个加密方法是以罗马共和时期恺撒的名字命名的，当年恺撒曾用此方法与其将军们进行联系。
原本字母表。 ABCDEFGHIJKLMNOPQRSTUVWXYZ
通过一个偏移量(也就是秘钥)，将字母表顺序改变。假设这里的秘钥是 +3
那么生成一个新字母表顺序。DEFGHIJKLMNOPQRSTUVWXYZABC
也就是 A->D,B->E,C->F,…,X->A,Y->B,Z->C

若秘钥是+N，就将字母往前数到N，此时对应的字母就是加密结果
若秘钥是-N，就将字母往后数到N，此时对应的字母就是加密结果
N超过26的可以将字母看成一个循环的圈

示例：

• 明文：LOVE
• 秘钥：Y1=+3，Y2=-6，Y3=-46
• 密文：QRYH，FIPY，SVCL

还一种将字母写成数字的解密小游戏。
$A=1，B=2，C=3，\cdots \cdots ，X=24，Y=25，Z=26$
给出一组数对{22，18，21，21，28，-3}，这是加密后的。
最后的-3表示在它之前的数字都减3，得到{19，15，18，18，25}，也就是SORRY的意思。此处的秘钥就是+3。

维吉尼亚密码

维吉尼亚方阵，一个加密的对照表。

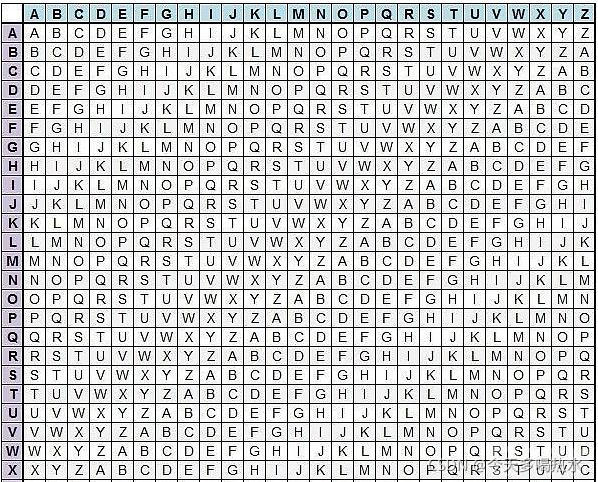
维吉尼亚方阵的使用方式大体如下：
（方阵是以对角线对称的，先行后列或者先列后行的加密效果是一样的。这里展示了先行后列的形式。）

示例：

• 明文：ILOVEYOU
• 秘钥：BIG
• 密文：JSUWMEPC

加密过程：
（1）明文字母依序排列，得到一行字母串 ILOVEYOU
（2）将秘钥写在明文字母串的下面。明文有多长，秘钥就写多长。不够的就循环补足，多的就删掉（一般不会多，毕竟删了，秘钥不就是剩余的那一个了么）
（3）得到如下排列 ：$\begin{array}{c}ILOVEYOU\\ BIGBIGBI\end{array}$
（4）对照方阵，对明文进行加密 (明文字母+秘钥字母–>密文字母)
（5）比如 (I+B->J)，(L+I->S)，(O+G->U)，(V+B->W)，(E+I->M)，，，得到密文：JSUWMEPC

除了查表，还可以通过计算得出结果。这种计算的方式能直观的感受出与恺撒密码的区别。 首先，将字母与数字一一对应，A->+0，B->+1，C->+2，D->+3，，Y->24，Z->25

其次也是要得到一个二行的排列：$\begin{array}{c}ILOVEYOU\\ BIGBIGBI\end{array}$
最后一步就是计算。如下;
I+B–>I+(+1)–>I前进1就是J，L+I–>L+(+8)–>L前进8就是S，O+G–>O+(+6)–>O前进6就是U，V+B–>V+(+1)–>V前进1就是W，，，
得到密文：JSUWMEPC

秘钥可以随意选取，一可以是一串毫无意义的字母序列

希尔密码

这里举个简单的例子，具体原理不太懂。。。
加密之前对26个字母进行编码，做一个密码字典：$A=0，B=1，C=2，\cdots \cdots ，X=23，Y=24，Z=25$
示例：

• 明文：LOVE
• 秘钥：Y= $\left(\begin{array}{cccc}1& 2& 3& 4\\ 1& 3& 4& 1\\ 1& 4& 1& 2\\ 1& 1& 2& 3\end{array}\right)$
• 密文：OLSB

加密过程：
（1）对照密码字典，对明文进行编码 L=11，O=14，V=21，E=4
（2）编码之后得到一个明文矩阵 M =$\left(\begin{array}{c}11\\ 14\\ 21\\ 4\end{array}\right)$
（3）求密文矩阵N，N等于明文矩阵左乘秘钥矩阵。即N=YM =$\left(\begin{array}{cccc}1& 2& 3& 4\\ 1& 3& 4& 1\\ 1& 4& 1& 2\\ 1& 1& 2& 3\end{array}\right)$$\left(\begin{array}{c}11\\ 14\\ 21\\ 4\end{array}\right)$
（4）得到N = $\left(\begin{array}{c}118\\ 141\\ 96\\ 79\end{array}\right)$
（5）把所有的数都除以26求余数。例：118/26=4余14，141/26=5余11
（6）得到新的密文矩阵N`= $\left(\begin{array}{c}14\\ 11\\ 18\\ 1\end{array}\right)$
（5）对照密码字典，进行反编译，也即是将数字转换为字母。14=O，11=L，18=S，1=B
（6）得到密文L：OLSB

作为秘钥的矩阵必须是可逆的