根据经纬度计算两地之间的距离

地球赤道周长：40075.02千米 ，地球平均半径：6371.393千米，圆周率：3.141592653589793（以上是百度的结果）

Haversine公式（半正矢公式）

原理分析

直接套公式，简洁高效。

球面余弦定理：
$d=R\times \arccos (\cos (纬度A)\cos (纬度B)\cos (经度A-经度B)+\sin (纬度A)\sin (纬度B))$

Haversine公式推导过程：
https://zhuanlan.zhihu.com/p/202993882?utm_source=wechat_session
https://www.douban.com/note/766524321/

Python代码

import math

R = 6371.393
Pi = math.pi

jingduA, weiduA= 116.295794, 39.890115
jingduB, weiduB = 121.400053, 31.212544

a = (math.sin(math.radians(weiduA/2-weiduB/2)))**2
b = math.cos(weiduA*Pi/180) * math.cos(weiduB*Pi/180) * (math.sin((jingduA/2-jingduB/2)*Pi/180))**2
L = 2 * R * math.asin((a+b)**0.5)

# 因为地球平均半径用的是千米，所以最后结果的单位也是千米
print(L)

SQL

最近涉及到用sql计算距离，来填补一下。以下代码Oracle和MySQL都能执行

-- 最后结果的单位是米 
with tmp as(
select 103.20887 lng1, 30.613502 lat1, 104.737777 lng2, 31.520277 lat2, acos(-1) pi from dual 
)
select d.lng1, d.lat1, d.lng2, d.lat2
,2*6371393*asin(sqrt(sin(d.deltaLat/2)*sin(d.deltaLat/2)+cos(d.lat1*pi/180)*cos(d.lat2*pi/180)*sin(d.deltaLng/2)*sin(d.deltaLng/2))) as dist_asin 
,6371393*acos(sin(d.lat1*pi/180)*sin(d.lat2*pi/180)+cos(d.lat1*pi/180)*cos(d.lat2*pi/180)*cos(d.deltaLng)) as dist_acos 
from (
select c.lng1,c.lat1, c.lng2, c.lat2, c.pi, 
(c.lat1*pi/180-c.lat2*pi/180) as deltaLat,(c.lng1*pi/180-c.lng2*pi/180) as deltaLng
from tmp c
) d;

向量法求两地距离

原理分析

思路：以地心为原点，建立空间直角坐标系。将地球上任意两点的经纬度坐标转为直角坐标。然后用向量求出夹角余弦值，最后用角度求弧长。
误差：地球不是完美的球体。

以地心为原点，建立空间直角坐标系：

X轴为地心到（经度：0°、纬度：0°）的向量
Y轴为地心到（经度：90°、纬度：0°）的向量
Z轴为地心到（纬度：90°）的向量

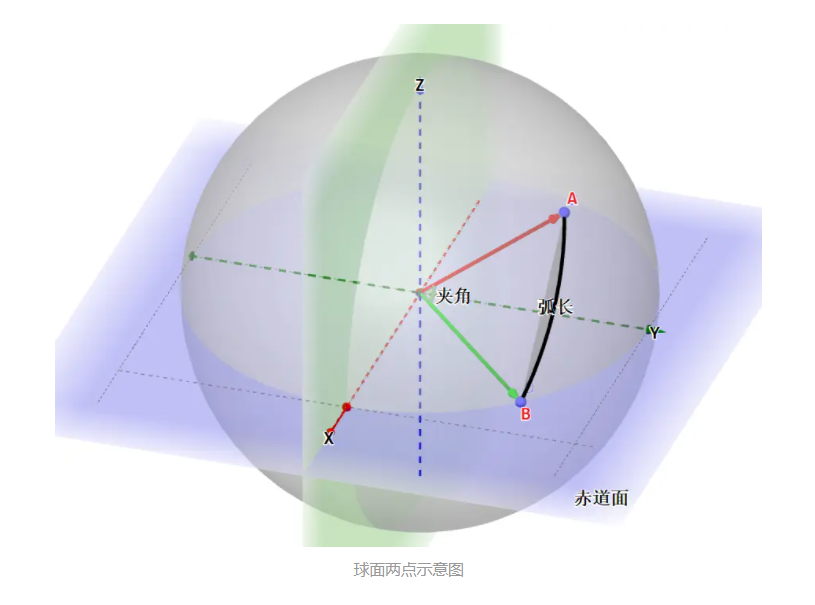
经纬度与空间直角坐标系的对应关系	地球两地间距离的示意图

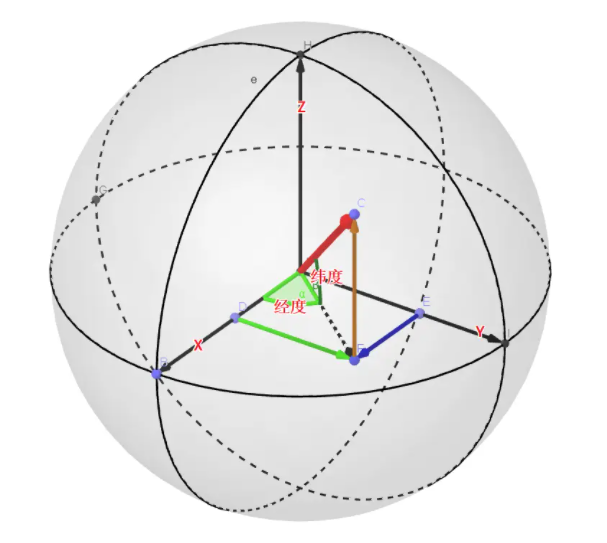由此可以得到由经纬度到空间直角坐标系的对应关系：

$x=\cos (纬度)\cos (经度)，y=\cos (纬度)\sin (经度)，z=\sin (纬度)$

由两个点对应的向量求出向量夹角：
$$\cos \theta =\frac{V_A\cdot V_B}{|V_A|\times |V_B|}\theta =\arccos (\frac{V_A\cdot V_B}{|V_A|\cdot |V_B|})$$

假设地球为理想球体：半径大约3959英里(6371.393千米) 。这个数字是地心到地球表面所有各点距离的平均值，平均半径=(赤道半径×2+极半径)/3。

则由半径和夹角可求弧长：
$$弧长l=\pi R\frac{\theta }{180}=\alpha R$$

其中$\theta$是圆心角度数（角度制），R是半径，L是圆心角弧长，$\alpha$是圆心角度数（弧度制）。$\alpha =\pi \theta /180$

Python代码

import math

R = 6371.393
Pi = math.pi

# A地
jingduA, weiduA= 116.295794, 39.890115
xA = math.cos(math.radians(weiduA))*math.cos(math.radians(jingduA))
yA = math.cos(math.radians(weiduA))*math.sin(math.radians(jingduA))
zA = math.sin(math.radians(weiduA))

# B地
jingduB, weiduB = 121.400053, 31.212544
xB = math.cos(weiduB*Pi/180) * math.cos(jingduB*Pi/180)
yB = math.cos(weiduB*Pi/180) * math.sin(jingduB*Pi/180)
zB = math.sin(weiduB*Pi/180)


# 开始计算
cosalpha = (xA*xB+yA*yB+zA*zB)/((xA*xA+yA*yA+zA*zA)*(xB*xB+yB*yB+zB*zB))**0.5

alpha = math.acos(cosalpha)
L = alpha * R

# 单位是千米
print(L)

知识补充

• 在经线上纬度差1度对应的实际距离是111.2018千米
• 在赤道上经度差1度对应的实际距离是111.3195千米
• 在除赤道外的其他纬线上，经度差1度对应的实际距离是111.3195*cos纬度

从理论上讲，全部的经线长度都相等，无论沿哪条经线南北极之间的距离都相等。
所以从理论上算，一条经线的长度=平均半径乘以圆周率=$\pi$R=20016.321441933433千米。所以，在同一条经线上，纬度差1度对应的实际距离是$\pi$R/180=111.20178578851908千米。

赤道周长: 40075020m。
因为赤道被分为了360度，所以在赤道上经度差1度对应的实际距离是40075020/360=111319.5m=111.3195km；对于纬度不为0的情况，在同一条纬线上，经度差1度对应的实际距离是111.3195$\times$cos纬度。
（另一种理论计算结果应该是111.2018$\times$cos纬度，因为平均半径R$\times$cos纬度等于该纬度对应的小圆半径（一条纬线就是一个圈，小圆说的就是这个圈），1度所对应的弧长就是2$\pi$R$\times$cos纬度/360=111.2018$\times$cos纬度）

总结，对于日常的学习生活来说，相差一度取111km、圆周率用3.14就够了，不必太过较真。

球坐标系与直角坐标系的转换

$$\begin{array}{r}\begin{array}{rl}x& =r\sin \theta \cos \varphi \\ y& =r\sin \theta \sin \varphi \\ z& =r\cos \theta \end{array}⟺\begin{array}{rl}r& =\sqrt{x^2+y^2+z^2}\\ \theta & =\arccos (\frac{z}{r})=\arcsin (\frac{\sqrt{x^2+y^2}}{r})=\arctan (\frac{\sqrt{x^2+y^2}}{z})\\ \varphi & =\arccos (\frac{x}{r\sin \theta })=\arcsin (\frac{y}{r\sin \theta })=\arctan (\frac{y}{x})\end{array}\end{array}$$

$径向距离r\in [0，+\infty ]，倾角(天顶角)\theta \in [0，\pi ]，方位角\varphi \in [0，2\pi ]$