预期分数:40 + 100 + 0 + 10 = 150
实际得分: 0 + 100 + 0 + 10 = 110
反思or收获
1.在暴力没拿满的情况下不要死磕一道题!
2.只有乘法的运算才能用log去压,如果有加法一定不要想用log去压!
chess:根据题意分析


如果暴力DP,发现字符串比较在最劣情况下为
O
(
n
)
O(n)
O(n),显然过不了,考虑转化问题,如果在 第
1
1
1步就不是最优的策略一定不会被用到第
2
2
2步,所以基于这个性质,我们可以考虑每一步最优为什么,将可以跑到最优的存入set,只用set里面的元素更新下一步的最优,这样的时间复杂度就转化为了
O
(
(
n
+
m
)
l
o
g
)
O((n + m)log)
O((n+m)log)
#include<bits/stdc++.h>
using namespace std;
const int MAX = 2100;
#define PII pair<int, int>
char ch[MAX][MAX];
char minn[MAX + MAX];
queue<PII> q;
set<PII> s[MAX + MAX];
int n, m;
int main() {
freopen("a.in","r",stdin);
freopen("a.out","w",stdout);
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
cin>>ch[i][j];
for(int i = 1; i <= n + m + 10; i++) minn[i] = 'z';
minn[1] = ch[1][1];
s[1].insert((PII){1, 1});
for(int i = 2; i <= n + m; i++) {
for(auto lst : s[i - 1]) {
int x = lst.first, y = lst.second;
if(x < n && minn[i] >= ch[x + 1][y]) {
if(minn[i] > ch[x + 1][y]) s[i].clear();
minn[i] = ch[x + 1][y];
s[i].insert((PII){x + 1, y});
}
if(y < m && minn[i] >= ch[x][y + 1]) {
if(minn[i] > ch[x][y + 1]) s[i].clear();
if(minn[i] > ch[x][y + 1]) minn[i] = ch[x][y + 1];
s[i].insert((PII){x, y + 1});
}
}
}
for(int i = 1; i <= n + m - 1; i++) {
cout<<minn[i];
}
return 0;
}
glass:简单装呀

数据范围,一眼状压,压什么? 我们发现一个瓶子只会被转移一次,且转移后一定不会再次转移,所以我们就压一个瓶子是否转移过即可,时间复杂度
O
(
2
n
∗
n
∗
n
)
O(2^n*n*n)
O(2n∗n∗n)跑不满,所以能过
//一个瓶子只会被转移
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int MAX = (1 << 21);
int n, k, ANS = 1e9;
int f[MAX], c[25][25];
int Minn[MAX][21];
int main() {
freopen("b.in","r",stdin);
freopen("b.out","w",stdout);
scanf("%d%d", &n, &k);
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
cin>>c[i][j];
}
}
memset(Minn, 0x3f, sizeof(Minn));
for(int i = 0; i <= (1 << n) - 1; i++) {
for(int j = 0; j < n; j++) {
if(i >> j & 1) continue;
for(int k = 0; k < n; k++) {
if(k != j) if((i >> k & 1) == 0) Minn[i][j] = min(Minn[i][j], c[j][k]);
}
}
}
memset(f, 0x3f, sizeof(f));
f[0] = 0;
for(int i = 0; i <= (1 << n) - 1; i++) {
for(int j = 0; j < n; j++) {
if((i >> j & 1) == 0) {
f[i | (1 << j)] = min(f[i | (1 << j)], f[i] + Minn[i][j]);
}
}
}
int ans = 1e9;
for(int i = 0; i <= (1 << n); i++) {
int sum = 0;
for(int j = 0; j < n; j++) {
if((i >> j & 1) == 0) sum++;
}
if(sum == k) ans = min(ans, f[i]);
}
cout<<ans<<endl;
return 0;
}
card:组合意义的DP


原题,但是之前没做,考场上也是一筹莫展
因为一个序列不同是操作顺序有一位不同即可,所以一定有组合意义,考虑如何将一个问题转化为一个组合问题
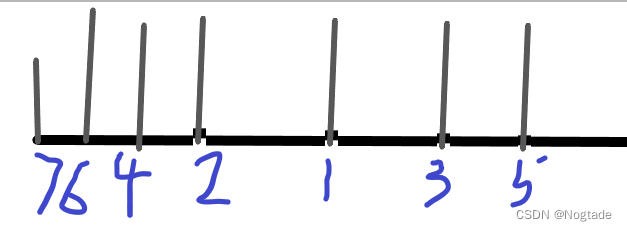
随意构造一个序列,我们发现根据题意操作
在
1
1
1左侧的数下标一定递减,在
1
1
1右侧的数下标递增
那么最大值是怎么统计的呢? 一定为左侧数的单调递增加上右侧数的单调递增的个数
但是要规定左侧的最大值,小于右侧单调递增的最小值
左侧单调递增在原序列中为以某个数(x)的单调递减序列
为了保证上述规定,右侧的单调递增的数也由x为起点,这样的话将总数减1即为最大严格递增子序列的长度
而总数如何计算,假设对于
x
x
x而言由若干个组合可以构成最大严格递增子序列,对于其它的数除了1以外,往左放,往右放都无所谓,所以答案
+
=
s
u
m
∗
(
2
n
−
l
e
n
+
1
/
2
)
1
+=sum*(2^{n-len+1}/2)1
+=sum∗(2n−len+1/2)1
而求最长上升子序列,最长下降子序列需要一个 ( l o g ) (log) (log)做法,离散化后值域线段树即可
//一个序列不同,当且仅当操作序列不同, 具有计数优势
//在1左边的下标递减, 值递增, 在1右边的下标递增, 值递增
//考虑用一个数划分阶段
#include<bits/stdc++.h>
using namespace std;
#define LL long long
//#define int long long
const int MOD = 1e9 + 7;
const int MAX = 2e5 + 70;
int n, a[MAX], b[MAX], tot;
LL num_up[MAX], num_down[MAX];
LL f_up[MAX], f_down[MAX];
int lsh[MAX];
struct node { int f, num; };
struct SegmentTree {
int l, r;
LL f, num;
#define l(x) tree[x].l
#define r(x) tree[x].r
#define f(x) tree[x].f
#define num(x) tree[x].num
}tree[MAX * 4];
LL quick_mi(int x, int y) {
LL xx = x, res = 1;
while(y) {
if(y & 1) res = res * xx % MOD;
xx = xx * xx % MOD;
y = y / 2;
}
return res;
}
void update(int p) {
if(f(2 * p) > f(2 * p + 1)) { f(p) = f(2 * p); num(p) = num(2 * p) % MOD; }
else if(f(2 * p + 1) > f(2 * p)) { f(p) = f(2 * p + 1); num(p) = num(2 * p + 1) % MOD; }
else if(f(2 * p + 1) == f(2 * p)) { f(p) = f(2 * p); num(p) = (num(2 * p) + num(2 * p + 1)) % MOD; }
return ;
}
void build(int p, int l, int r) {
l(p) = l, r(p) = r, f(p) = num(p) = 0;
if(l == r) { return ; }
int mid = (l + r) >> 1;
build(2 * p, l, mid);
build(2 * p + 1, mid + 1, r);
}
node New(node x, node y) {
if(x.f > y.f) return x;
else if(y.f > x.f) return y;
node NOW; NOW.f = x.f; NOW.num = (x.num + y.num) % MOD;
return NOW;
}
node Find(int p, int l, int r) {
if(l(p) >= l && r(p) <= r) {
node NOW; NOW.f = f(p); NOW.num = num(p);
return NOW;
}
node NOW; NOW.f = 0, NOW.num = 0;
int mid = (l(p) + r(p)) >> 1;
if(l <= mid) NOW = New(NOW, Find(2 * p, l, r));
if(r > mid) NOW = New(NOW, Find(2 * p + 1, l, r));
return NOW;
}
void change(int p, int l, int r, int ff, int num) {
if(l(p) == r(p)) {
if(ff > f(p)) {
f(p) = ff;
num(p) = num % MOD;
} else if(ff == f(p)) {
num(p) = (num(p) + num) % MOD;
}
return ;
}
int mid = (l(p) + r(p)) >> 1;
if(mid >= l) change(2 * p, l, r, ff, num);
if(r > mid) change(2 * p + 1, l, r, ff, num);
update(p);
}
void Clear() { for(int i = 0; i <= 8e5 + 1; i++) tree[i].f = tree[i].num = 0; }
signed main() {
freopen("c.in","r",stdin);
scanf("%d", &n);
for(int i = 1; i <= n; i++) {
scanf("%d", &a[i]); b[i] = a[i];
}
sort(b + 1, b + 1 + n);
for(int i = 1; i <= n; i++) if(b[i] != b[i - 1]) lsh[++tot] = b[i];
for(int i = 1; i <= n; i++) a[i] = lower_bound(lsh + 1, lsh + 1 + tot, a[i]) - lsh;
reverse(a + 1, a + 1 + n);
build(1, 0, 2e5 + 1);
change(1, 2e5 + 1, 2e5 + 1, 0, 1);
for(int i = 1; i <= n; i++) {
node NOW = Find(1, a[i] + 1, 2e5 + 1);
f_up[i] = NOW.f + 1;
num_up[i] = NOW.num % MOD;
change(1, a[i], a[i], f_up[i], num_up[i]);
}
Clear();
change(1, 0, 0, 0, 1);
for(int i = 1; i <= n; i++) {
node NOW = Find(1, 0, a[i] - 1);
f_down[i] = NOW.f + 1;
num_down[i] = NOW.num % MOD;
change(1, a[i], a[i], f_down[i], num_down[i]);
}
LL maxx = 0, NUM = 0;
for(int i = 1; i <= n; i++) {
if(f_up[i] + f_down[i] - 1 > maxx) { maxx = f_up[i] + f_down[i] - 1; NUM = 0; }
if(f_up[i] + f_down[i] - 1 == maxx) NUM = (NUM + (1LL * num_up[i] * num_down[i] % MOD * quick_mi(2, n - f_up[i] - f_down[i] + 1) % MOD) ) % MOD;
}
cout<<maxx<<' '<<NUM<<endl;
return 0;
}
godnumber:锅


ACAM套数位DP,还没打




















 65
65











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








