文章目录
前言
这章主要讲容斥原理。
一、引言
- 容斥原理是组合数学中的一个重要原理,它在计数问题中占有很重要地位。
- 容斥原理所研究的问题是与若干有限集的交、并或差有关的计数。
- 在实际工作中,有时要计算具有某种性质的元素个数。
【例】某单位举办一个外语培训班,开设英语、法语两门课。
- 设U为该单位所有人集合,A、B分别为学英语、法语人的集合,如图所示。
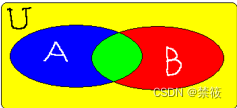
- 学两门外语的人数为 ∣ A ⋂ B ∣ |A\bigcap B| ∣A⋂B∣,只学一门外语的人数为 ∣ A ⋃ B ∣ − ∣ A ⋂ B ∣ |A\bigcup B|-|A\bigcap B| ∣A⋃B∣−∣A⋂B∣,没参加学习的人数为 ∣ U ∣ − ∣ A ⋃ B ∣ |U|-|A\bigcup B| ∣U∣−∣A⋃B∣。
在一些计数问题中,经常遇到间接计算一个集合中具有某种性质的元素个数比起直接计算来得简单。
【例】计算1到700之间不能被7整除的整数个数。
- 直接计算相当麻烦,间接计算非常容易。
- 先计算1到700之间能被7整除的整数个数 = 700 7 = 100 =\frac{700}{7}=100 =7700=100,所以1到700之间不能被7整除的整数个数 = 700 − 100 = 600 =700-100=600 =700−100=600。
- 因此,当直接求解受阻或无法达到目的时,应考虑间接求解方法。所谓”曲径通幽“,说的就是这个道理。
- 上面举得间接计数的例子是利用了如下原理:如果A是集合S的子集,则A中的元素个数等于S中的元素个数减去不在A中的元素个数。该原理可写成
∣
A
∣
=
∣
S
∣
−
∣
A
‾
∣
或
∣
A
‾
∣
=
∣
S
∣
−
∣
A
∣
|A|=|S|-|\overline{A}|或|\overline{A}|=|S|-|A|
∣A∣=∣S∣−∣A∣或∣A∣=∣S∣−∣A∣其中
A
‾
\overline{A}
A表示
A
A
A在
S
S
S中的
补集或余集。
二、容斥原理
DeMorgan(德·摩根)定理:设A,B为全集U的任意两个子集,则 A ∪ B ‾ = A ‾ ∩ B ‾ \overline{A\cup B}=\overline{A}\cap \overline{B} A∪B=A∩B A ∩ B ‾ = A ‾ ∪ B ‾ \overline{A\cap B}=\overline{A}\cup \overline{B} A∩B=A∪B
DeMorgan(德·摩根)定理的推广: 设 A 1 , A 2 , ⋯ , A n A_1,A_2,\cdots,A_n A1,A2,⋯,An为U的子集,则 A 1 ∪ A 2 ∪ ⋯ ∪ A n ‾ = A 1 ‾ ∩ A 2 ‾ ∩ ⋯ ∩ A n ‾ \overline{A_1\cup A_2\cup\cdots\cup A_n}=\overline{A_1}\cap\overline{A_2}\cap\cdots\cap\overline{A_n} A1∪A2∪⋯∪An=A1∩A2∩⋯∩An A 1 ∩ A 2 ∩ ⋯ ∩ A n ‾ = A 1 ‾ ∪ A 2 ‾ ∪ ⋯ ∪ A n ‾ \overline{A_1\cap A_2\cap\cdots\cap A_n}=\overline{A_1}\cup\overline{A_2}\cup\cdots\cup\overline{A_n} A1∩A2∩⋯∩An=A1∪A2∪⋯∪An
1、两个集合的容斥原理
设A和B是分别具有性质 P 1 P_1 P1和 P 2 P_2 P2的元素的集合,则 ∣ A ∪ B ∣ = ∣ A ∣ + ∣ B ∣ − ∣ A ∩ B ∣ |A\cup B|=|A|+|B|-|A\cap B| ∣A∪B∣=∣A∣+∣B∣−∣A∩B∣
【例】求1到500之间能被5或7整除的正整数个数。
解:设A为被5整除的整数集合,B为被7整除的整数集合,用
[
x
]
[x]
[x]表示x的整数部分,则有

2、三个集合上的容斥原理
设A,B,C为任意三个集合,则有 ∣ A ∪ B ∪ C ∣ = ∣ A ∣ + ∣ B ∣ + ∣ C ∣ − ∣ A ∩ B ∣ − ∣ A ∩ C ∣ − ∣ B ∩ C ∣ + ∣ A ∩ B ∩ C ∣ |A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C| ∣A∪B∪C∣=∣A∣+∣B∣+∣C∣−∣A∩B∣−∣A∩C∣−∣B∩C∣+∣A∩B∩C∣
3、n个集合上的容斥原理
设 A 1 , A 2 , ⋯ , A n A_1,A_2,\cdots,A_n A1,A2,⋯,An是有限集合,则有 ∣ A 1 ∪ A 2 ∪ ⋯ ∪ A n ∣ = ∑ i = 1 n ∣ A i ∣ − ∑ i = 1 n ∑ j > i ∣ A i ∩ A j ∣ + ∑ i = 1 n ∑ j > i ∑ k > j ∣ A i ∩ A j ∩ A k ∣ − ⋯ + ( − 1 ) n − 1 ∣ A 1 ∩ A 2 ∩ ⋯ ∩ A n ∣ |A_1\cup A_2\cup\cdots\cup A_n|=\displaystyle\sum_{i=1}^n|A_i|-\displaystyle\sum_{i=1}^n\displaystyle\sum_{j>i}|A_i\cap A_j|+\displaystyle\sum_{i=1}^n\displaystyle\sum_{j>i}\displaystyle\sum_{k>j}|A_i\cap A_j\cap A_k|-\cdots+(-1)^{n-1}|A_1\cap A_2\cap \cdots\cap A_n| ∣A1∪A2∪⋯∪An∣=i=1∑n∣Ai∣−i=1∑nj>i∑∣Ai∩Aj∣+i=1∑nj>i∑k>j∑∣Ai∩Aj∩Ak∣−⋯+(−1)n−1∣A1∩A2∩⋯∩An∣
4、容斥原理的余集形式
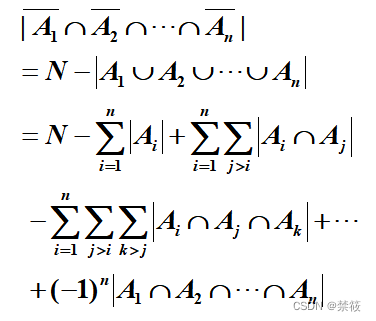
5、例题



以下为无编号入座方法数:



三、容斥原理的应用实例
1、错排问题
- 上一讲利用递归关系讨论了错排问题,现在利用容斥原理再次讨论这个问题。
- 可以看出容斥原理解决这个问题更容易,而且利用容斥原理很容易理解错排数列通项公式的组合意义。
- 我们再重申一下,排列 i 1 , i 2 , ⋯ , i n i_1,i_2,\cdots,i_n i1,i2,⋯,in是排列 1 , 2 , ⋯ , n 1,2,\cdots,n 1,2,⋯,n的一个错排当且仅当 i 1 ≠ 1 , i 2 ≠ 2 , ⋯ , i n ≠ n i_1\ne1, i_2\ne2,\cdots,i_n\ne n i1=1,i2=2,⋯,in=n。
- 我们曾把
1
,
2
,
⋯
,
n
1,2,\cdots,n
1,2,⋯,n全部不同错排的数目记为
D
n
D_n
Dn。当时得到的结论如下:
D
n
=
n
!
(
1
−
1
1
!
+
1
2
!
−
1
3
!
+
⋯
+
(
−
1
)
n
1
n
!
)
D_n=n!(1-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+\cdots+(-1)^n\frac{1}{n!})
Dn=n!(1−1!1+2!1−3!1+⋯+(−1)nn!1)
D
n
=
n
!
∑
k
=
0
n
(
−
1
)
k
1
k
!
D_n=n!\displaystyle\sum_{k=0}^n(-1)^k\frac{1}{k!}
Dn=n!k=0∑n(−1)kk!1


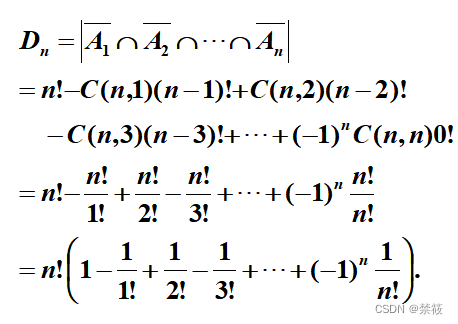

2、有限制的排列
所谓有限制的排列,就是对排列加上某种或某些限制。


3、相对禁位排列
在错排问题中,每个元素不许出现在原来的位置,这是一种绝对的禁位排列。还有一类是相对禁位排列。





Q
n
=
∣
A
1
‾
∩
A
2
‾
∩
⋯
∩
A
n
‾
∣
=
∑
k
=
0
n
−
1
(
−
1
)
k
C
(
n
−
1
,
k
)
(
n
−
k
)
!
Q_n=|\overline{A_1}\cap\overline{A_2}\cap\cdots\cap\overline{A_n}|=\displaystyle\sum_{k=0}^{n-1}(-1)^kC(n-1,k)(n-k)!
Qn=∣A1∩A2∩⋯∩An∣=k=0∑n−1(−1)kC(n−1,k)(n−k)!


4、欧拉函数



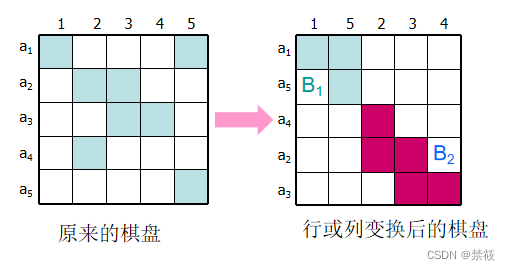
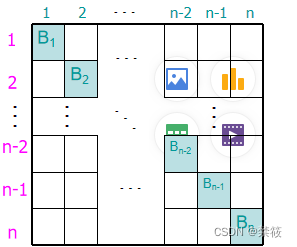
5、棋盘多项式
5.1、棋盘布局问题

5.2、需要注意的问题

5.3、例题


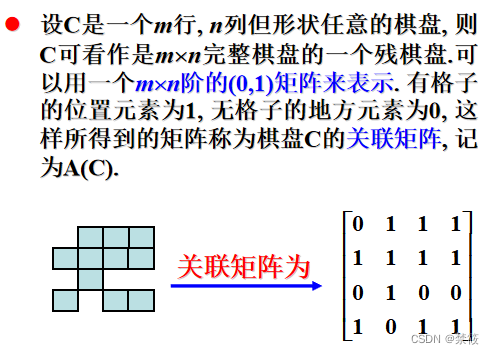
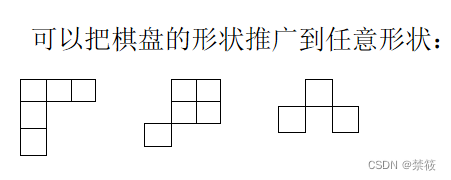

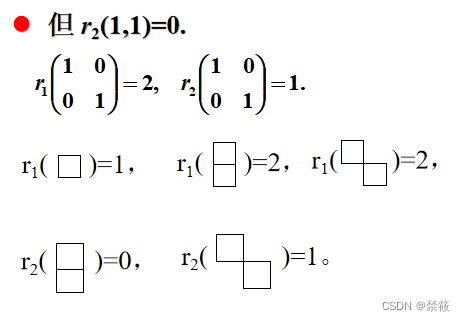
5.4、棋盘多项式的定义(母函数)





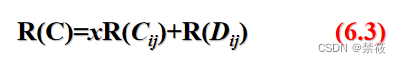







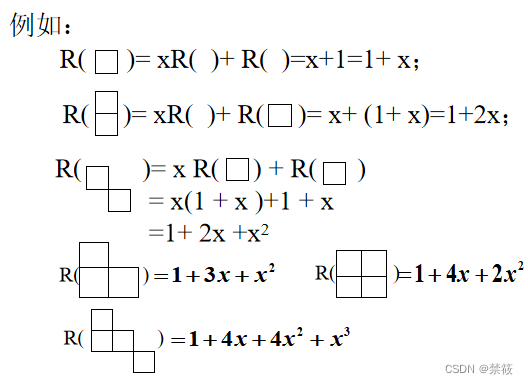

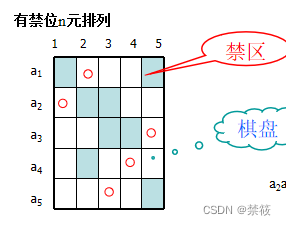
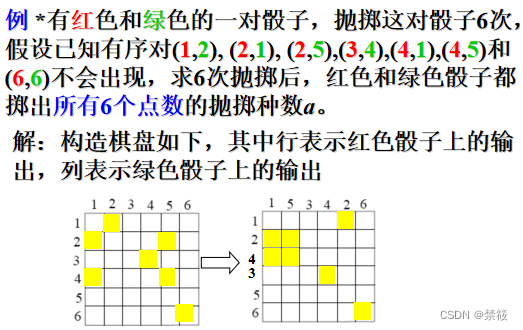
6、禁位排列
所谓”禁位排列“是指在一个排列中禁止某些元素占据某些位置。
错排是禁位排列的一种特殊情况。


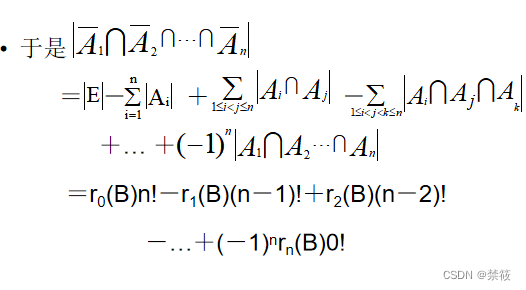





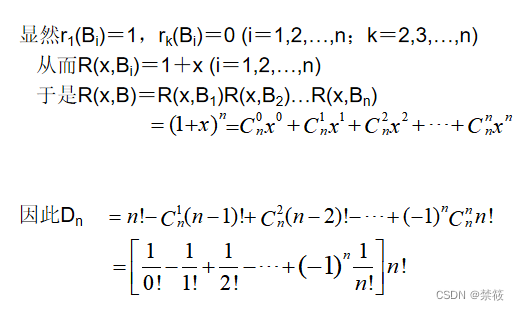























 8568
8568











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










