一、前言
聚类分析是根据在数据中发现的描述对象及其关系的信息,将数据对象分组,它是一种重要的人类行为。 聚类分析的目标就是在相似的基础上收集数据来分类,聚类源于很多领域,包括数学,计算机科学,统计学,生物学和经济学。它的目的是,组内的对象相互之间是相似的(相关的),而不同组中的对象是不同的(不相关的)。组内相似性越大,组间差距越大,说明聚类效果越好。
不同的聚类算法有不同的应用背景,有的适合于大数据集,可以发现任意形状的聚簇;有的算法思想简单,适用于小数据集。K-means算法是最常用的一种聚类算法。算法的输入为一个样本集(或者称为点集),通过该算法可以将样本进行聚类,具有相似特征的样本聚为一类。
二、K-means算法和原理
2.1K-Means算法
K-Means算法是最为经典的基于划分的聚簇方法,是十大经典数据挖掘算法之一。简单的说K-Means就是在没有任何监督信号的情况下将数据分为K份的一种方法。聚类算法就是无监督学习中最常见的一种,给定一组数据,需要聚类算法去挖掘数据中的隐含信息。K值是聚类结果中类别的数量。简单的说就是我们希望将数据划分的类别数。
K-means聚类能处理比层次聚类更大的数据集。另外,观测值不会永远被分到一类中,当我们提高整体解决方案时,聚类方案也会改动。不过不同于层次聚类的是,K-means会要求我们事先确定要提取的聚类个数。
2.2K-Means算法基本思想
在数据集中根据一定策略选择K个点作为每个簇的初始中心,然后观察剩余的数据,将数据划分到距离这K个点最近的簇中,也就是说将数据划分成K个簇完成一次划分,但形成的新簇并不一定是最好的划分,因此生成的新簇中,重新计算每个簇的中心点,然后在重新进行划分,直到每次划分的结果保持不变。
但是在实际应用中往往经过很多次迭代仍然达不到每次划分结果保持不变,甚至因为数据的关系,根本就达不到这个终止条件,实际应用中往往采用变通的方法设置一个最大迭代次数,当达到最大迭代次数时,终止计算。
2.3K-Means适用范围及缺陷
K-Menas算法试图找到使平方误差准则函数最小的簇。当潜在的簇形状是凸面的,簇与簇之间区别较明显,且簇大小相近时,其聚类结果较理想。对于处理集合、球形数据,该算法非常高效,且伸缩性较好。
但是,该算法除了要事先确定簇数K和对初始聚类中心敏感外,经常以局部最优结束,同时对“噪声”和孤立点敏感,并且该方法不适于发现非凸面形状的簇或大小差别很大的簇。
克服缺点的方法:使用尽量多的数据;使用中位数代替均值来克服outlier的问题。
三、K-means算法步骤
(1)根据具体问题,凭条件从样本集中选出个K个比较合适的样本作为初始聚类中心;
(2)求出每个样本到中心点的距离,按照距离自身最近的中心点进行第一次聚类;
(3)根据新划分的簇,更新“簇中心”;
(4)重复上述2、3过程,直至"簇中心"没有移动,或小于给定阈值。

图例
原始数据:

聚类处理后的数据:

四、原题复现:
问题描述:利用k-means聚类对下列数据(仅展示部分,第三列为待改进的原始类别)进行分类,我们可以通过选择不同的k值来比较模型的好坏。

K-means聚类实现源代码:
1.自定义函数代码:
import numpy as np
import math as m
import random
import matplotlib.pyplot as plt
import evaluate as eva # 自定义的模型评估包
# 导入数据
def load_data(data_path):
points = np.loadtxt(data_path, delimiter='\t')
return points
# 计算质点与数据点的距离
def cal_dis(data, clu, k):
"""
:param data: 样本点
:param clu: 质点集合
:param k: 类别个数
:return: 质心与样本点距离矩阵
"""
dis = []
for i in range(len(data)):
dis.append([])
for j in range(k): # 计算数据点距离K个质心的距离
dis[i].append(m.sqrt((data[i, 0] - clu[j, 0])**2 + (data[i, 1]-clu[j, 1])**2))
return np.asarray(dis)
# 将所有样本分配到最近的中心点
def divide(data, dis):
"""
:param data: 样本集合
:param dis: 质心与所有样本的距离
:param k: 类别个数
:return: 分割后样本
"""
clusterRes = [0] * len(data)
for i in range(len(data)):
seq = np.argsort(dis[i])
clusterRes[i] = seq[0]
return np.asarray(clusterRes)
# 重新计算中心点
def center(data, clusterRes, k):
"""
:param group: 分组后样本
:param k: 类别个数
:return: 计算得到的质心
"""
clunew = []
for i in range(k):
# 计算每个组的新质心
idx = np.where(clusterRes == i)
sum = data[idx].sum(axis=0)
avg_sum = sum/len(data[idx])
clunew.append(avg_sum)
clunew = np.asarray(clunew)
return clunew[:, 0: 2]
# 迭代收敛更新质心
def classfy(data, clu, k):
"""
:param data: 样本集合
:param clu: 质心集合
:param k: 类别个数
:return: 误差, 新质心
"""
clulist = cal_dis(data, clu, k) # 计算数据距离K个质心的距离
clusterRes = divide(data, clulist) # 将数据点分配到最近的质心
clunew = center(data, clusterRes, k) #重新计算中心点
err = clunew - clu # 计算新旧质心的偏移
return err, clunew, k, clusterRes
def plotRes(data, clusterRes, clusterNum):
"""
结果可视化
:param data:样本集
:param clusterRes:聚类结果
:param clusterNum: 类个数
:return:
"""
nPoints = len(data)
scatterColors = ['black', 'blue', 'green', 'yellow', 'red', 'purple', 'orange', 'brown']
for i in range(clusterNum):
color = scatterColors[i % len(scatterColors)]
x1 = []; y1 = []
for j in range(nPoints):
if clusterRes[j] == i:
x1.append(data[j, 0])
y1.append(data[j, 1])
plt.scatter(x1, y1, c=color, alpha=1, marker='+')
plt.show()
if __name__ == '__main__':
k = 7 # 类别个数
data = load_data() # 导入数据,见函数定义
clu = random.sample(data[:, 0:2].tolist(), k) # 随机取K个质心
clu = np.asarray(clu) # 注意array与asarray的区别
err, clunew, k, clusterRes = classfy(data, clu, k)
while np.any(abs(err) > 0):
print(clunew)
err, clunew, k, clusterRes = classfy(data, clunew, k) # 见classify函数的定义
clulist = cal_dis(data, clunew, k)
clusterResult = divide(data, clulist)
nmi, acc, purity = eva.eva(clusterResult, np.asarray(data[:, 2]))
print(nmi, acc, purity)
plotRes(data, clusterResult, k)2.调用Sklearn库实现代码:
from sklearn.cluster import KMeans
from sklearn import metrics
from yellowbrick.cluster import SilhouetteVisualizer
X_data=data[:, 0:2]
y_label=data[:, 2]
# 调库实现K-means聚类
km = KMeans(n_clusters=3, random_state=42) # 随机选取3个聚类中心
km.fit_predict(X_data)
score = metrics.silhouette_score(X_data, km.labels_, metric='euclidean')
print('Silhouetter Score: %.3f' % score)
fig, axs = plt.subplots(3, 2, figsize=(15,8))
# 利用sklearn库里自带函数画图分析选取不同类别聚类效果
for i in np.arange(6):
#Create KMeans instance for different number of cluster
km = KMeans(n_clusters=i+3, init='k-means++', n_init=10, max_iter=100, random_state=42)
q, mod = divmod(i, 2)
#print(i,q,mod)
visualizer = SilhouetteVisualizer(km, colors='yellowbrick', ax=axs[q][mod])
visualizer.fit(X_data)
visualizer.show() 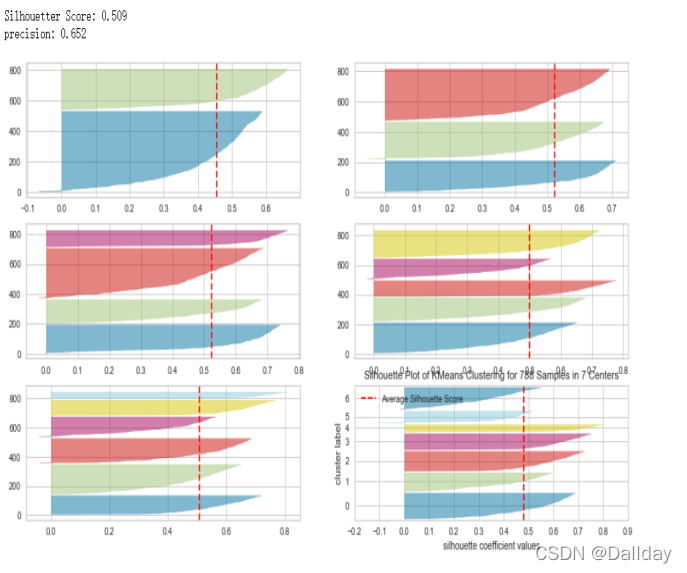








 本文详细介绍了K-means聚类算法,包括其基本原理、适用场景与局限性,以及如何通过K-means对数据进行分类。重点展示了K-means算法的步骤,并通过实例演示了如何使用Python实现,包括自定义函数和Scikit-learn库的应用。
本文详细介绍了K-means聚类算法,包括其基本原理、适用场景与局限性,以及如何通过K-means对数据进行分类。重点展示了K-means算法的步骤,并通过实例演示了如何使用Python实现,包括自定义函数和Scikit-learn库的应用。
















 1128
1128

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








