你好呀~我是陌陌❀❀❀

1. 二叉树概述
二叉树(Binary tree)是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式,即使是一般的树也能简单地转换为二叉树,而且二叉树的存储结构及其算法都较为简单,因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树,且有左右之分 。
二叉树是n个有限元素的集合,该集合或者为空、或者由一个称为根(root)的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成,是有序树。当集合为空时,称该二叉树为空二叉树。在二叉树中,一个元素也称作一个节点
2. 二叉树遍历
2.1 递归实现
/**
* 递归实现前、中、后序的遍历
* @param head
*/
public static void f(Node head){
if(head == null){
return;
}
//1. 先序
f(head.left);
//2. 中序
f(head.right);
//3. 后序
}
2.2 非递归实现
一切递归都可以转换为非递归!!!
2.2.1 前序遍历
/**
* 非递归实现先序遍历
* @param head
*/
public static void preOrderUnRecur(Node head){
if(head != null){
Stack<Node> stack = new Stack<Node>();
stack.add(head);
while(!stack.isEmpty()){
head = stack.pop();
System.out.println(head.value+" ");
if(head.right != null){
stack.add(head.right);
}if(head.left != null){
stack.push(head.left);
}
}
}
}
2.2.2 中序遍历
/**
* 非递归实现中序遍历
* @param head
*/
public static void inOrderUnRecur(Node head){
if(head != null){
Stack<Node> stack = new Stack<>();
while(!stack.isEmpty() || head != null){
if(head != null){
stack.push(head);
head = head.left;
}else{
head = stack.pop();
System.out.println(head.value + " ");
head = head.right;
}
}
}
}
2.2.3 后续遍历
/**
* 非递归实现后续遍历
*/
public static void posOrderUnRecur1(Node head){
if(head == null){
return;
}
Stack<Node> stack1 =new Stack<>();
Stack<Node> stack2 =new Stack<>();
stack1.add(head);
while(!stack1.isEmpty()){
head = stack1.pop();
stack2.push(head);
if(head.left != null){
stack1.push(head.left);
}
if(head.right != null){
stack1.push(head.right);
}
}
while(!stack2.isEmpty()){
System.out.println(stack2.pop().value +" ");
}
}
2.3 广度优先遍历
/**
* 广度优先遍历
* @param head
*/
public static void w(Node head){
if(head == null){
return;
}
Queue<Node> queue = new LinkedList<Node>();
queue.add(head);
while(!queue.isEmpty()){
Node cur = queue.poll();
System.out.println(cur.value);
if(cur.left != null){
queue.add(cur.left);
}
if(cur.right != null){
queue.add(cur.right);
}
}
}
3. 相关练习
3.1 练习
练习一:二叉树层结点最大数
计算一颗二叉树某层中结点个数最大的个数和
和下一题的区别在于,我计算的是每一层的结点数目,然后返回结点数最大值就可以了,而下一道题是最大的宽度,换句话说计算的是每层第一个结点和最后一个结点的索引差
//计算一颗二叉树中某一层中结点个数最大的数字
public static int w1(Node head){
if(head == null){
return 0;
}
Queue<Node> queue = new LinkedList<Node>();
queue.add(head);
HashMap<Node,Integer> levelMap = new HashMap<>();
levelMap.put(head,1);
int curLevel = 1;
int curLevelNods = 0;
int max = Integer.MIN_VALUE;
while(!queue.isEmpty()){
Node cur = queue.poll();
int curNodeLevel = levelMap.get(cur);
if(curNodeLevel == curLevel){
curLevelNods++;
}else{
max = Math.max(max,curLevelNods);
curLevel++;
curLevelNods=1;
}
if(cur.left != null){
levelMap.put(cur.left,curNodeLevel+1);
queue.add(cur.left);
}
if(cur.right != null){
levelMap.put(cur.right,curNodeLevel+1);
queue.add(cur.right);
}
}
return max;
}
练习二:最大宽度
给你一棵二叉树的根节点 root ,返回树的 最大宽度 。
树的 最大宽度 是所有层中最大的 宽度 。
每一层的 宽度 被定义为该层最左和最右的非空节点(即,两个端点)之间的长度。将这个二叉树视作与满二叉树结构相同,两端点间会出现一些延伸到这一层的 null 节点,这些 null 节点也计入长度。
题目数据保证答案将会在 32 位 带符号整数范围内。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int widthOfBinaryTree(TreeNode head) {
//1. head二叉树有至少一个结点
int res = 1;
List<Pair<TreeNode,Integer>> arr = new ArrayList<Pair<TreeNode,Integer>>();
arr.add(new Pair<TreeNode,Integer>(head,1));
while(!arr.isEmpty()){
List<Pair<TreeNode,Integer>> tmp = new ArrayList<Pair<TreeNode,Integer>>();
for(Pair<TreeNode,Integer> pair : arr){
TreeNode node = pair.getKey();
int index = pair.getValue();
if(node.left != null){
tmp.add(new Pair<TreeNode,Integer>(node.left,index * 2));
}
if(node.right != null){
tmp.add(new Pair<TreeNode,Integer>(node.right ,index * 2 + 1));
}
}
res = Math.max(res,arr.get(arr.size() - 1).getValue() - arr.get(0).getValue() + 1);
arr = tmp;
}
return res;
}
}
练习三:搜索二叉树
如何判断一颗二叉树是否是搜索树:
搜索树:若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值
/**
* 判断是否是搜索二叉树
* @return
*/
public static boolean checkBST(Node head){
if(head == null){
return true;
}
boolean isLeftBST = checkBST(head.left);
if(!isLeftBST){
return false;
}
if(head.value <= preValue){
return false;
}else{
preValue = head.value;
}
return checkBST(head.right);
}
练习四 :完全二叉树
如何判断一颗树是否是完全二叉树
完全二叉树:一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树
/**
* 判断一颗二叉树是否是完全二叉树
*/
//使用宽度优先遍历,
//1. 遇到的任何一个结点只有右孩子没有左孩子,淘汰
//2. 如果遇到了第一个左右两个孩子不双全的情况,接下来遇到的所有结点都必须是叶子结点
public static boolean isCBT(Node head){
if(head == null){
return true;
}
LinkedList<Node> queue = new LinkedList<>();
//是否遇到过左右两个孩子不双全的结点
boolean leaf = false;
Node l = null;
Node r = null;
while(!queue.isEmpty()){
head = queue.poll();
l = head.left;
r = head.right;
if(
(leaf && (l != null || r != null))
||
(l == null && r != null)
){
return false;
}
if(l != null){
queue.add(l);
}
if(r != null){
queue.add(r);
}
if( l == null || r == null){
leaf = true;
}
}
return true;
}
练习五 :满二叉树
如何判断一颗树是否是满二叉树
满二叉树:除最后一层无任何子节点外,每一层上的所有结点都有两个子结点的二叉树。
/**
* 判断一颗树是否是满二叉树
*/
//1. 方法一:先求二叉树的最大深度,再求树中结点个数
//2. 方法二:按套路来~👇
public static class Info{
public int height;
public int nodes;
public Info(int hei,int nods){
height = hei;
nodes = nods;
}
}
public static Info fB(Node head){
if(head == null){
return new Info(0,0);
}
Info l = fB(head.left);
Info r = fB(head.right);
int height = Math.max(l.height,r.height) + 1;
int nodes = l.nodes + r.nodes + 1;
return new Info(height,nodes);
}
public static boolean isF(Node head){
if(head == null){
return true;
}
Info f = fB(head);
return f.nodes == f.height << 1 + 1;
}
练习六:平衡二叉树
如何判断一颗二叉树是平衡二叉树
平衡二叉树:平衡二叉树,又称AVL树,用于解决二叉排序树高度不确定的情况,如果二叉排序树的子树间的高度相差太大,就会让二叉排序树操作的时间复杂度升级为O(n),为了避免这一情况,为最坏的情况做准备,就出现了平衡二叉树,使树的高度尽可能的小,其本质还是一棵二叉搜索树。
/**
* 判断一颗树是否是平衡二叉树
* 对于任何一个子树来说,它左树的高度和右树的高度差都不超过1
*/
public static class ReturnType{
public boolean isBalanced;
public int height;
public ReturnType(boolean isB,int hei){
isBalanced = isB;
height = hei;
}
}
public static boolean isBalance(Node head){
return process(head).isBalanced;
}
public static ReturnType process(Node x){
if(x == null){
return new ReturnType(true,0);
}
ReturnType leftData = process(x.left);
ReturnType rightData = process(x.right);
int height = Math.max(leftData.height,rightData.height);
boolean isBalance = leftData.isBalanced && rightData.isBalanced && Math.abs(leftData.height-rightData.height) < 2;
return new ReturnType(isBalance,height);
}
练习七:公共父节点
求一颗二叉树中某两个结点的公共父节点
① 方法一:
使用Map集合,假设要求o1和o2的公共父节点
- 将每一个结点的父节点都存入Map集合中
- 设置Set集合,先将o1的路径存放到Set集合中去
- 再将设置Set集合,存放o2的路径,在存放o2的过程中,同时判断o2中路径中的结点是否在o1路径集合中,如果存在返回该结点,如果不存在返回head结点
public static Node lca(Node head,Node o1,Node o2){
HashMap<Node,Node> fatherMap = new HashMap<>();
process(head,fatherMap);
HashSet<Node> set1 = new HashSet<>();
Node cur = o1;
while(cur != fatherMap.get(cur)){
set1.add(cur);
cur = fatherMap.get(cur);
}
cur = o2;
set1.add(head);
while(!set1.contains(cur)){
//得到当前结点的父节点
cur = fatherMap.get(cur);
}
return cur;
}
public static void process(Node head,HashMap<Node,Node> fatherMap){
if(head == null){
return;
}
fatherMap.put(head.left,head);
fatherMap.put(head.right,head);
process(head.left,fatherMap);
process(head.right,fatherMap);
}
② 方法二
这个方法就很牛逼,最好是画图来食用
- 首先o1和o2的情况有两种
- 两个结点一个是另一个的父节点
- 两个结点有公共的父节点,但肯定不是对方
- 看图片
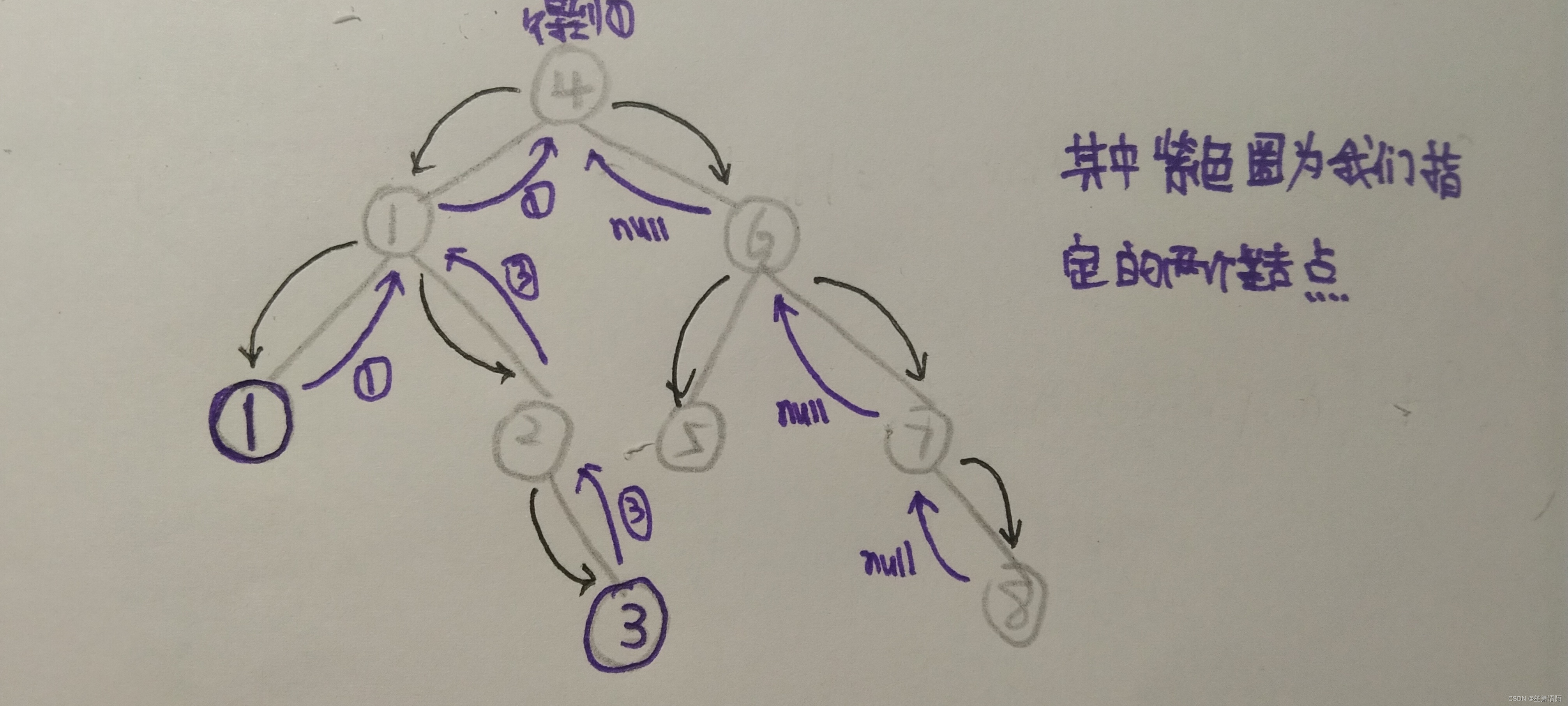
解释一下该图片,其中黑色路线为父节点向字节点索要结果
紫色路线为子节点给父节点返回的结果
可以对照它来解读下面的代码
/**
* 找到O1,O2两个结点的公共祖先
* 1. 首先o1和o2的情况右两种
* 1. o1 和 o2互为父节点
* 2. O1 和 o2不互为父节点
*/
public static Node lowestAncestor(Node head,Node o1,Node o2){
if(head == null || head == o1 || head == o2){
return head;
}
Node left = lowestAncestor(head.left,o1,o2);
Node right = lowestAncestor(head.right, o1,o2);
if(left != null && right != null){
return head;
}
return left != null ? left : right;
}
3.2 小结
大部分的二叉树的题目都可以归为一个套路:
我需要什么?为了得到结果我需要和子节点要什么信息?
然后将需要的信息封装为一个类,逐层返回即可






















 158
158

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








