青蛙跳台阶问题（Java语言）

题目

一只青蛙一次可以跳上 1 级台阶，也可以跳上2 级。求该青蛙跳上一个n 级的台阶总共有多少种跳法？

解析

这类题目乍一看简单易懂，但是给人一种无从下手的感觉，既然如此，我们先举一些简单的例子：
当只有1级台阶时(当n=1)：

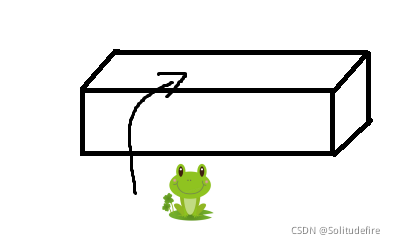
青蛙只需要跳一节台阶就可以了，因此只有一种跳法。
当只有2级台阶时(当n=2)：

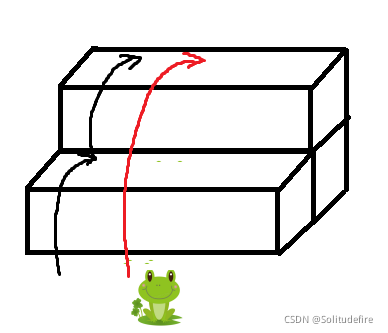
青蛙有两种跳法：1+1（第一种，黑色线），2（第二种，红色线）。
当有3级台阶时(当n=3)：

青蛙有3种跳法：1+1+1（第一种，黑色线），2+1（第二种，红色线），1+2（第三种，绿色线）。
当有4节台阶（当n=4）：

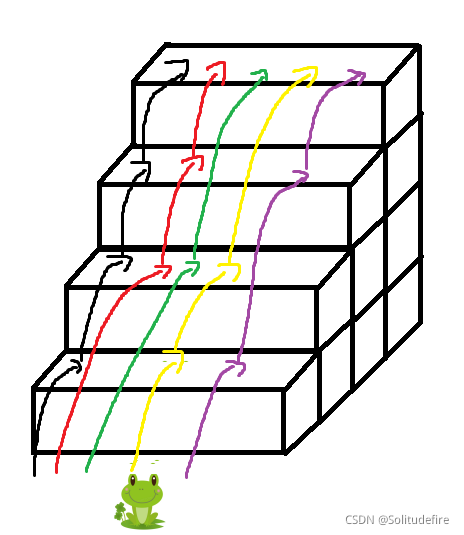
青蛙有5种跳法：1+1+1+1+1（第一种，黑色线），2+1+1（第二种，红色线），2+2（第三种，绿色线），1+1+2（第四种，黄色线），1+2+1（第五种，紫色线）。
我们以n=4为例，我们看当n=4时一共有五种跳法，首先我们假设青蛙先跳1节台阶，那么还剩下3级台阶，此时有3种台阶的跳法（当n=3），我们再假设青蛙跳2节台阶，那么还剩下2级台阶，此时有2种台阶跳法（当n=2）。因此n=4时，就是青蛙先跳1节台阶后的跳法，再加上青蛙先跳2节台阶的跳法。也就是说f（4）=f（3）（青蛙先跳1节台阶后的跳法）+f（2）（青蛙先跳2节台阶后的跳法）。通过分析我们知道，f（n）=f（n-1）+f（n-2）。并且f（1）=1，f（2）=2。

代码实现

递归版本：

public static int fun(int n) {
        if (n == 1) {
            return 1;
        }else if(n==2){
            return 2;
        }else{
            return fun(n-2)+fun(n-1);
        }
    }
    public static void main(String[] args) {
        System.out.println(fun(4));
    }

非递归版本：

public static int fun(int n) {
        if (n == 1 || n == 2) {
            return n;
        }
        int f1 = 1;
        int f2 = 2;
        int f3 = 0;
        for (int i = 3; i <= n; i++) {
            f3 = f1 + f2;
            f1 = f2;
            f2 = f3;
        }
        return f3;
    }
    public static void main(String[] args) {
        System.out.println(fun(4));
    }

青蛙跳台问题就是一种斐波那契数列的变体，有关斐波那契数列问题，有兴趣的同学可以看一看瞅一瞅，如果这次的博客有所帮助，别忘了点赞关注呦，谢谢各位啦！如有问题欢迎各位私信评论。