目录
引言:
在这个日新月异的技术时代,电工电子技术作为现代工业和信息化社会的基石,其重要性不言而喻。作为一名电子工程师或技术爱好者,我们每天都在与电路图、电子元件和信号处理打交道。但在这个过程中,我们是否真正理解了每一个知识点背后的原理?是否能够在每一次学习后,都能有所收获,有所领悟?“一课一得”不仅仅是一个学习的理念,它更是一种追求深度理解和实践应用的态度。
在本系列博客中,我将与你一同探索《电工电子技术》的每一个知识点,从基础的电路理论到复杂的电子系统设计,我们不仅仅是学习,更是在每一次学习中寻找那个“得”——那个能够让我们的技术能力更上一层楼的领悟点。让我们一起开启这段知识之旅,期待在每一篇文章的末尾,我们都能有所收获,都能对自己的技术之路有更深的认识。
电工技术理论
电工电子技术是一门涉及电能的产生、传输、分配、使用以及电子设备的设计、开发和应用的综合性工程技术学科。它结合了电工技术和电子技术两个领域,前者主要关注电力系统的运行和维护,后者则侧重于电子信号的处理和电子设备的开发。以下是电工电子技术的基本概念和理论基础:
电工技术基础
-
电路理论:
描述电路中电压、电流和电阻之间的关系,包括欧姆定律、基尔霍夫电压定律(KVL)和基尔霍夫电流定律(KCL)。 -
电磁学:
研究电场和磁场的性质,以及它们如何相互作用,包括法拉第电磁感应定律和麦克斯韦方程组。 -
电力系统:
涉及电力的生成、传输和分配,包括发电站、变压器、输电线路和配电网络。 -
电机学:
研究电机的工作原理,包括直流电机、交流电机和特种电机。 -
电力电子:
涉及电力电子器件(如二极管、晶体管、MOSFET、IGBT等)和电力电子转换技术。
电子技术基础
-
模拟电子技术:
包括放大器、滤波器、振荡器等基本电子电路的设计和分析。 -
数字电子技术:
涉及数字逻辑电路的设计,包括逻辑门、触发器、计数器、寄存器等。 -
半导体器件:
研究二极管、晶体管、集成电路等半导体器件的工作原理和应用。 -
信号与系统:
研究信号的表示、处理和传输,包括连续时间信号和离散时间信号。 -
通信原理:
涉及信息传输的基本原理,包括调制解调技术、信道编码和信号处理。 -
微处理器和微控制器:
研究微处理器和微控制器的架构、编程和应用。 -
传感器技术:
涉及各种传感器的工作原理和它们在数据采集中的应用。
电路的基本概念与分析方法
欧姆定律
欧姆定律是指在同一电路中,通过某段导体的电流跟这段导体两端的电压成正比,跟这段导体的电阻成反比。该定律是由德国物理学家乔治·西蒙·欧姆1826年4月发表的《金属导电定律的测定》论文提出的。科尔劳施使用Dellmann静电计在1849年研究了欧姆定律 。
欧姆定律可以用以下公式表示:
| 条件 | 电压 (V) | 电阻 (Ω) | 电流 (A) |
|---|---|---|---|
| 示例 1 | 10 | 5 | 2 |
| 示例 2 | 20 | 10 | 2 |
| 示例 3 | 5 | 2.5 | 2 |
其中:
- V表示电压(单位:伏特,V),
- I 表示电流(单位:安培,A),
- R 表示电阻(单位:欧姆,Ω)。
欧姆定律的三个主要形式如下:
电流与电压的关系: I=VRI=RV 当电阻 RR 保持不变时,通过导体的电流 II 与导体两端的电压 VV 成正比。
电流与电阻的关系: I=VRI=RV 当电压 VV 保持不变时,通过导体的电流 II 与导体的电阻 RR 成反比。
电压与电阻的关系: V=IRV=IR 当电流 II 保持不变时,导体两端的电压 VV 与导体的电阻 RR 成正比。

欧姆定律适用于线性电路,即电阻值不随电压或电流的变化而变化的电路。对于非线性电路,欧姆定律不适用,因为电阻值会随着电压或电流的变化而变化。

例如,欧姆定律计算器的Python
def ohm_law_calculator(voltage, resistance):
current = voltage / resistance
return current
voltage = float(input("输入电压 (V): "))
resistance = float(input("输入电阻 (Ω): "))
current = ohm_law_calculator(voltage, resistance)
print(f"电流为: {current:.2f} A")
基尔霍夫定律
基尔霍夫定律(Kirchhoff's laws)是电路中电压和电流所遵循的基本规律,是分析和计算较为复杂电路的基础。该定律由德国物理学家G.R.基尔霍夫(Gustav Robert Kirchhoff)在1845年提出,包括基尔霍夫电流定律(KCL)和基尔霍夫电压定律(KVL)。
| 定律名称 | 描述 | 数学表达式 | 应用场景 |
|---|---|---|---|
| 基尔霍夫电流定律 (KCL) | 电路中任意节点,流入节点的电流之和等于流出节点的电流之和。 | ∑Iin=∑Iout∑Iin=∑Iout | 节点分析 |
| 基尔霍夫电压定律 (KVL) | 电路中任意闭合回路,电压降的代数和等于零。 | ∑V=0∑V=0 | 回路分析 |
基尔霍夫电流定律(KCL):
应用于电路中的节点,节点指的是电路中三个或两个以上的支路相连接的点。
指出对于电路中的任何一个节点而言,在任何一个时间,流进节点的电流等于流出节点的电流;即节点电流之代数和恒等于0。
| 节点编号 | 流入电流 (A) | 流出电流 (A) | 电流关系式 |
|---|---|---|---|
| 节点A | I1 | I2 | I1=I2 |
| 节点B | I3 | I4,I5 | I3=I4+I5 |

基尔霍夫电压定律(KVL):
在任何一个闭合回路中,各元件上的电压降的代数和等于电动势的代数和,即从一点出发绕回路一周回到该点时,各段电压的代数和恒等于零,即∑U=0。
表明沿着闭合回路所有元件两端的电势差(电压)的代数和等于零,或者描述为沿着闭合回路的所有电动势的代数和等于所有电压降的代数和。
| 回路编号 | 电压降 (V) | 电压关系式 |
|---|---|---|
| 回路1 | V1,V2V1,V2 | V1−V2=0V1−V2=0 |
| 回路2 | V3,V4,V5V3,V4,V5 | V3+V4−V5=0V3+V4−V5=0 |

实验验证
基尔霍夫定律可以通过实验进行验证。实验中,可以通过测量电路中各节点的电流和各回路的电压,验证它们是否符合KCL和KVL的描述。

具体实验步骤包括连接电路、测量电流和电压、记录数据、计算并比较结果等。通过实验验证,可以更深入地理解基尔霍夫定律在电路分析中的应用和重要性。

例如,基尔霍夫电压定律(KVL)的Python代码如下:
def kirchhoff_voltage_law(v1, v2, v3, i):
return abs(v1 + v2 - v3 - i * 10) < 1e-6
v1 = 12.0
v2 = 5.0
v3 = 7.0
i = 1.0
if kirchhoff_voltage_law(v1, v2, v3, i):
print("满足基尔霍夫电压定律")
else:
print("不满足基尔霍夫电压定律")
相量表示法
相量的定义:相量是按照角速度以逆时针方向旋转的旋转矢量,用于表示正弦量的大小和相位。相量通常用大写字母上加“.”来标记,以区别于非旋转的矢量。
相量与正弦量的关系:相量与正弦量是一一对应的,可以通过相量的模和幅角,以及已知的角频率组成正弦量的瞬时值表达式。相量的模表示正弦量的有效值,而相量的辐角表示正弦量的初相位。
| 概念 | 描述 | 公式或表示法 |
|---|---|---|
| 相量 | 表示正弦波的幅度和相位的复数。 | |
| 幅度 | 相量的长度,代表正弦波的最大值或有效值。 | |
| 相位角 | 相量与实轴之间的角度,表示正弦波的相位。 | |
| 正弦波 | 时间的函数,表示电压或电流随时间的变化。 | |
| 相量加法 | 两个相量相加,相当于它们对应的正弦波的相量和。 | |
| 相量减法 | 两个相量相减,相当于它们对应的正弦波的相量差。 | |
| 相量乘法 | 两个相量相乘,相当于它们对应的正弦波的幅度乘积和相位和。 | |
| 阻抗 | 交流电路中电阻、电感和电容对电流的阻碍作用的相量表示。 | |
| 导纳 | 阻抗的倒数,表示电路对电流的导通能力。 | |
| 功率 | 交流电路中的平均功率,包括有功功率和无功功率。 |
相量法的应用:相量法主要用于分析正弦稳态电路,它将描述正弦稳态电路的微分(积分)方程变换成复数代数方程,从而简化了电路的分析和计算。在正弦稳态下,基尔霍夫定律中的电流和电压都是正弦量,用相量代表正弦电流和电压后,基尔霍夫电流定律(KCL)和基尔霍夫电压定律(KVL)分别变成相量形式的定律。
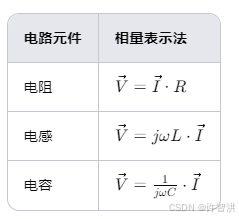
注:在这些表格中,j 表示虚数单位,ωω 是角频率,R 是电阻,L 是电感,C是电容,P是功率,V 是电压,I是电流,ϕ 是电压和电流之间的相位差。
相量图:相量图是表示相量的一种方式,它在复平面上用一个矢量来表示相量。相量图可以直观地展示各正弦量之间的相位关系,且不同频率的相量不能画在同一张相量图上,也就是说不同频率的相量之间不能进行运算。
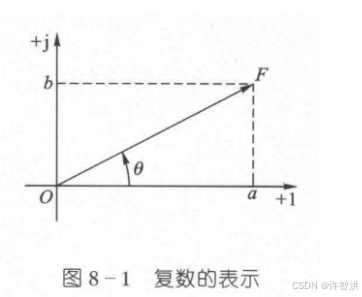
相量的运算:相量的加、减运算既可通过复数运算进行,也可在相量图上按矢量加、减法则进行。正弦量与它的相量是一一对应的,因此求出了相量就不难写出原来需要求的正弦量。
相量形式的电路定律:在正弦稳态下,基尔霍夫定律中的电流和电压都是正弦量。用相量代表正弦电流和电压后,基尔霍夫电流定律(KCL)和基尔霍夫电压定律(KVL)分别变成相量形式的定律,这使得电路分析更加简便。
电路元器件
基本电路元器件:
电阻器 (Resistor):限制电流流动,分压或产生热量。

电容器 (Capacitor):存储电荷,用于滤波、耦合、旁路、能量存储等。

电感器 (Inductor):存储磁能,用于滤波、振荡电路、变压器等。

二极管 (Diode):允许电流单向流动,用于整流、保护、限幅等。

晶体管 (Transistor):放大或开关电子信号,分为双极型晶体管(BJT)和场效应晶体管(FET)。

运算放大器 (Operational Amplifier, Op-Amp):高增益放大器,用于信号放大、滤波、比较等。
变压器 (Transformer):改变电压和电流的大小,用于隔离和能量传输。
继电器 (Relay):用小电流控制大电流的开关,用于远程控制和保护。

保险丝 (Fuse):过流保护,当电流超过一定值时熔断以保护电路。

开关 (Switch):控制电路的通断。

晶闸管 (Thyristor):可控整流器,用于交流电路的开关和调节。
光电耦合器 (Optocoupler):实现电气隔离,用于信号传输和保护。
传感器 (Sensor):检测物理量并转换为电信号,如温度、光、压力等。
集成电路 (Integrated Circuit, IC):将多个电子元件集成在一个芯片上,实现复杂功能。

核心电路元器件:
电阻器:用于控制电流和电压,是电路设计中最基本的元件。

电容器:在滤波、去耦、定时和能量存储等方面至关重要。

电感器:在滤波、振荡和能量存储中发挥重要作用。

二极管:在整流、保护和信号处理中不可或缺。

晶体管:作为放大器和开关,是构建复杂电子系统的基础。

运算放大器:在信号处理和放大中非常关键,应用广泛。

集成电路:现代电子设备中的核心,集成了复杂的功能。
注:
二极管、三极管的差异
功能差异
二极管:主要功能是允许电流在一个方向上流动,即从阳极流向阴极,而在反向时几乎不导电。二极管常用于整流、稳压、限幅和保护电路中12。
三极管:具有放大功能,可以将小信号放大到较高的电压或电流。它还常用于开关和振荡器电路中。三极管通过控制基极电流来调节集电极和发射极之间的电流,实现放大和开关功能。
应用领域差异
二极管:广泛应用于整流电路中,将交流电转换为直流电;在稳压电路中保持电压稳定;在限幅电路中限制信号幅度;在保护电路中防止过电压或反极性损害。
数字电路基础
-
基本概念和定义:
- 数字电路是指由逻辑门和触发器等基本逻辑元件组成的电路,用于处理和传输数字信号。数字电路通过将输入信号转换为离散的数字形式,并通过逻辑门的组合和触发器的状态变化来实现各种逻辑功能和运算。
-
逻辑门电路:
- 逻辑门是数字电路的基本构建块,执行基本的逻辑操作。常见的逻辑门包括与门(AND)、或门(OR)、非门(NOT)、异或门(XOR)和同或门(XNOR)等。
-
逻辑代数基础:
- 掌握逻辑函数的基本公式和常用公式,如交换律、结合律和分配律。熟悉同一律、摩根定律以及否定的性质。能够利用逻辑函数的基本公式和常用公式化简逻辑函数。
-
逻辑函数的化简方法:
- 通过合并项法和吸收法,将复杂的逻辑函数化简为最简的与或表达式。掌握卡诺图和波形图化简和分析逻辑函数的方法。
-
触发器及时序逻辑电路:
- 触发器是时序逻辑电路的基本单元,常见的触发器包括RS触发器、D触发器、JK触发器和T触发器等。这些触发器通过时钟信号控制其状态的变化,实现各种时序逻辑功能。
-
编码器和译码器:
- 编码器将多个输入信号转换为少数几个输出信号,常见的有普通编码器和优先编码器。译码器则将少数输入信号转换为多个输出信号,实现解码功能。
-
数据选择器和数据分配器:
- 数据选择器从多个输入信号中选择一个输出,而数据分配器则将一个输入信号分配到多个输出。这些器件在多路传输中起到重要作用。
-
其他重要概念:
- 格雷码是一种二进制编码方式,用于减少在数字系统中因状态变化引起的干扰。卡诺图是一种图形化工具,用于化简逻辑函数。
结尾
随着本篇博客的结束,我们对《电工电子技术》的探索也暂时告一段落。但学习永无止境,每一次的“一课一得”都是我们技术成长的见证。希望这些分享能够帮助你在电工电子技术的道路上越走越远,也希望它们能够激发你对技术的热爱和对知识的渴望。
在未来的日子里,让我们继续保持这种“一课一得”的学习态度,不断探索、不断实践、不断进步。如果你有任何疑问或者想要深入讨论的话题,欢迎在评论区留下你的想法,让我们一起交流,一起成长。记住,每一次学习都是一次新的开始,每一次领悟都是一次新的飞跃。让我们期待下一次的“一课一得”,期待在电工电子技术的世界里,遇见更好的自己。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








