幻方
幻方简介
起源:易经
别名:河图,洛书,纵横图。

-
定义:幻方是一种将数字安排在正方形格子中使每行,列和对角线上的数字都相等的方法。
种类:
-
完全幻方:一个幻方行,列,主对角线及范对角线各数之和均相等。
-
乘幻方:指一个幻方行,列对角线个数乘积相等。
-
高次幻方:高次幻方指,当组成幻方各数替换为其2,3,……,k,……次幂时,仍满足幻方条件的。
-
n阶幻方:指由前n^2个自然数组成的一个n阶方阵,各行各列及两条对角线所含的n个数的和相等。
如三阶幻方:
8 1 6 3 5 7 4 9 2 -
反幻方:在一个由若干个排列整齐的数组成的正方形中,其中任意一横行、一纵行及对角线的几个数之和不相等,具有这种性质的图表,称为“反幻方”。
-
幻方的制作(完全)
奇数幻方
方法二:杨辉法
九子斜排,上下对易,左右相更,四维推进;戴九履一,左三右气,二四为肩,六八为足。
解释:
九子斜排,
| 1 | ||||
|---|---|---|---|---|
| 4 | 2 | |||
| 7 | 5 | 3 | ||
| 8 | 6 | |||
| 9 |
上下对易,左右相更
| 9 | ||||
|---|---|---|---|---|
| 4 | 2 | |||
| 3 | 5 | 7 | ||
| 8 | 6 | |||
| 1 |
四维推进
| 4 | 9 | 2 | ||
| 3 | 5 | 7 | ||
| 8 | 1 | 6 | ||
方法二:罗伯法(楼梯法)
:一居上行正中央,依次斜填切莫忘;上出框时向下放,右出框时向左放;排重便在下格填,右上排重一个样。
代码
一居上行正中央:将数字1放到幻方第一行,中间一列
| 0 | 1 | 0 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 0 | 0 |
依次斜填切莫忘,上出框时向下放,右出框时向左放:从第一个数1开始,向左上(或右上)填数字,从上边超出边界时,放到最下面一行对应的列,重左边超出边界时,放到最右面一行对应的列。
| 0 | 1 | 0 |
|---|---|---|
| 0 | 0 | 3 |
| 2 | 0 | 0 |
排重便在下格填,右上排重一个样:如果要填入的数字被占了,则填到基准数字的下面。(如数字4的填法)
| 0 | 1 | 0 |
|---|---|---|
| 0 | 0 | 3 |
| 2 | 0 | 4 |
代码如下:
#include<iostream>
using namespace std;
int main()
{
int n,a[100][100]={0},x,y,i,j,k;
cin>>n;
j=n/2;
i=0;
a[i][j]=1;
for(k=2;k<=n*n;k++)
{
x=--i;
y=--j;
if(i<0)
i=n-1;
if(j<0)
j=n-1;
if(a[i][j]!=0)
{
i=x+2;
j=y+1;
}
a[i][j]=k;
}
for(i=0;i<n;i++)
{
for(j=0;j<n;j++)
{
cout<<a[i][j]<<"\t";
}
cout<<endl<<endl;
}
return 0;
}
双偶幻方(阶数为4的整数倍):
方法:Spring法
-
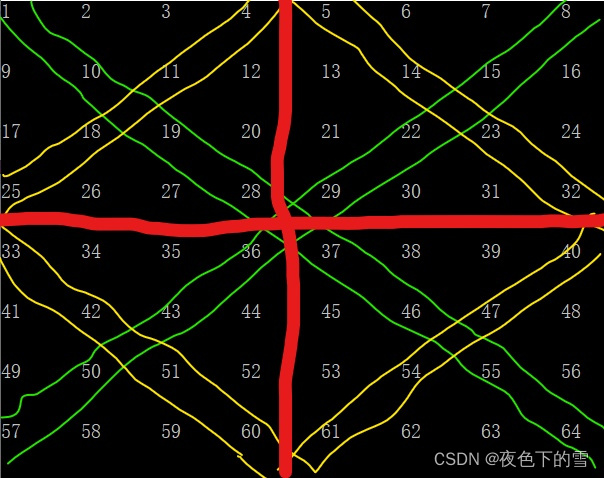
先按顺序将数字填到幻方框架中(以8阶幻方为例)。
如下图

-
然后将将数字分为4个小正方形(如图红线所分)后小正方形对角线上的数字,在大正方形上以中心对称的方式进行交换,(就是将原来的数字m换为数字n*n+1-m)(n为阶乘数)
-
2交换完成就得到幻方

#include<iostream>
#include<math.h>
using namespace std;
int a[100][100];
void two_even_numbers(int n)//双偶数幻方 4*n
{
int num=1;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
a[i][j]=num++;//按顺序输入
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
{
if(i%4==0&&abs(i-j)%4==0)
for(int k=0;k<=3;k++)
{
a[i+k][j+k]=n*n+1-a[i+k][j+k];//给小四边形的对角线赋值,由左上至右下
}
if(i%4==3&&(i+j)%4==3)
for(int k=0;k<=3;k++)
{
a[i-k][j+k]=n*n+1-a[i-k][j+k];//给小四边形的对角线赋值,由左下至右上
}
}
}
int main ()
{
int n;
cin>>n;
two_even_numbers(n);
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
cout<<a[i][j]<<"\t";
cout<<endl<<endl<<endl;
}
return 0;
}
单偶幻方(4n+2):斯特雷奇法
-
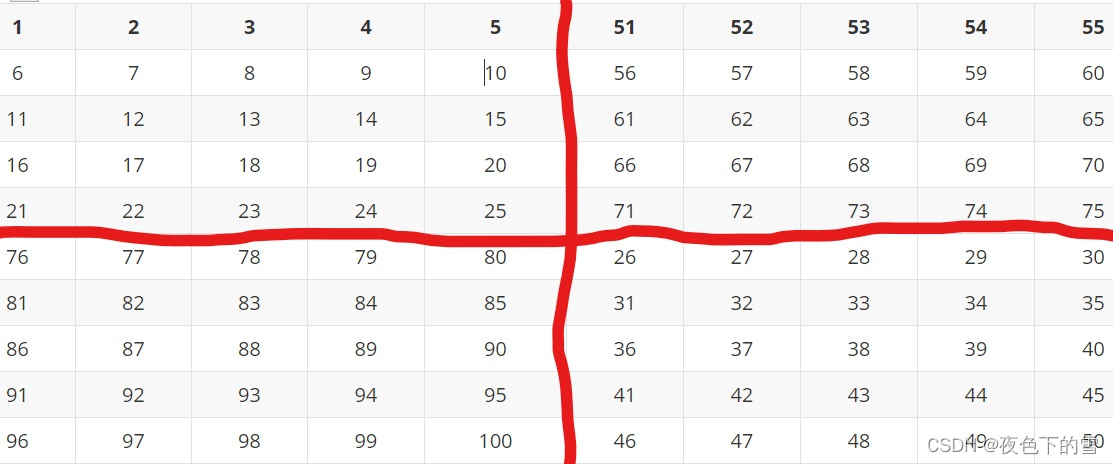
首先将n阶幻方分为四个区域,1为左上,2为右下,3为右上,4为左下,然后按区域按顺序填入数字。
-
然后将每个区域数字按奇数阶幻方的填法进行填表。(如下)
-

-
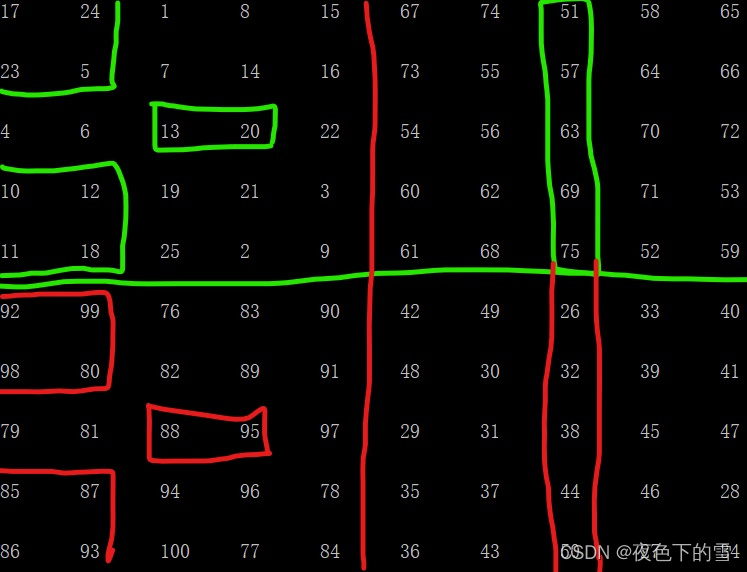
然后将绿色框内的数字和红色框内的对应位置的数字交换。
-
交换完成后得到幻方。
-

代码如下
//斯特雷奇法
#include<iostream>
#include<math.h>
using namespace std;
int a[100][100]={0};
//罗伯法,填小奇数幻方
int change1(int begin_point_x,int begin_point_y,int end_point_x,int end_point_y,int length,int number)
{
int k,z,w;
//赋值起点坐标
int i=begin_point_x;
int j=begin_point_y+length/2;
//赋起点值
a[i][j]=number;
//构造幻方
for(k=++number;k<=number+length*length-2;k++)//判断循环次数
{
z=i,w=j;
i--;
j++;
z=i,w=j;
if(i<begin_point_x) //判断是否出界
i=end_point_x;
if(j>end_point_y)//
j=begin_point_y;
//判断该位置是否有被赋值
if(a[i][j]!=0)
{
i=z+2;
j=w-1;
}
a[i][j]=k;
}
}
//进行位置交换
void change2(int n)
{
int k=(n-2)/4;
int t;
for(int i=0;i<n/2;i++)
{
for(int j=0;j<k;j++)//左半边幻方进行交换
{
if(i==n/4)
{
t=a[i][j+k];
a[i][j+k]=a[i+n/2][j+k];
a[i+n/2][j+k]=t;
}
else
{
t=a[i][j];
a[i][j]=a[i+n/2][j];
a[i+n/2][j]=t;
}
}
for(int j=0;j<k-1;j++)//右半边幻方进行交换
{
int m=j+n/2+n/4;
t=a[i][m];
a[i][m]=a[i+n/2][m];
a[i+n/2][m]=t;
}
}
}
int judge(int n)//判断输出是否正确
{
int num1=0,k=1,num2=0;
for(int i=0;i<n;i++)
num1+=a[0][i];
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
num2+=a[i][j];
}
if(num2!=num1)
k=0;
num2=0;
}
for(int j=1;j<n;j++)
{
for(int i=0;i<n;i++)
{
num2+=a[i][j];
}
if(num2!=num1)
k=0;
num2=0;
}
return k;
}
int main()
{
int n;
cin>>n;
int num=n/2;
//左上区
change1(0,0,num-1,num-1,n/2,1);
change1(num,num,n-1,n-1,n/2,num*num+1);
change1(0,num,num-1,n-1,n/2,num*num*2+1);
change1(num,0,n-1,num-1,n/2,num*num*3+1);
change2(n);
if(judge(n)==0)
cout<<"error"<<endl;
else
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
cout<<a[i][j]<<"\t";
}
cout<<endl<<endl<<endl;
}
return 0;
}
任意阶幻方
#include<iostream>
#include<math.h>
using namespace std;
int a[100][100];
//罗伯法,构造奇数幻方小奇数幻方
int change1(int begin_point_x,int begin_point_y,int end_point_x,int end_point_y,int length,int number)
//初始点坐标,结束点坐标,阶数,初始数据
{
int k,z,w;
//赋值起点坐标
int i=begin_point_x;
int j=begin_point_y+length/2;
//赋起点值
a[i][j]=number;
//构造幻方
for(k=++number;k<=number+length*length-2;k++)//判断循环次数
{
z=i,w=j;
i--;
j++;
z=i,w=j;
if(i<begin_point_x) //判断是否出界
i=end_point_x;
if(j>end_point_y)//
j=begin_point_y;
//判断该位置是否有被赋值
if(a[i][j]!=0)
{
i=z+2;
j=w-1;
}
a[i][j]=k;
}
}
//在使用罗伯法对单偶幻方的四个部分处理后,使用此法进行位置交换,构造双偶幻方
void change2(int n)
{
int k=(n-2)/4;
int t;
for(int i=0;i<n/2;i++)
{
for(int j=0;j<k;j++)//左半边幻方进行交换
{
if(i==n/4)
{
t=a[i][j+k];
a[i][j+k]=a[i+n/2][j+k];
a[i+n/2][j+k]=t;
}
else
{
t=a[i][j];
a[i][j]=a[i+n/2][j];
a[i+n/2][j]=t;
}
}
for(int j=0;j<k-1;j++)//右半边幻方进行交换
{
int m=j+n/2+n/4;
t=a[i][m];
a[i][m]=a[i+n/2][m];
a[i+n/2][m]=t;
}
}
}
//双偶幻方函数,海尔法
void two_even_numbers(int n)
{
int num=1;
//初始化数据
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
a[i][j]=num++;
//进行交换
int m=n*n+1;
int k;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
{
if(i%4==0&&abs(i-j)%4==0)
for(int k=0;k<4;k++)
{
a[i+k][j+k]=m-a[i+k][j+k];
}
else if(i%4==3&&(i+j)%4==3)
for(int k=0;k<4;k++)
{
a[i-k][j+k]=m-a[i-k][j+k];
}
}
}
//判断是否为幻方
int judge(int n)
{
int num1=0,k=1,num2=0;
for(int i=0;i<n;i++)
num1+=a[0][i];
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
num2+=a[i][j];
}
if(num2!=num1)
k=0;
num2=0;
}
for(int j=1;j<n;j++)
{
for(int i=0;i<n;i++)
{
num2+=a[i][j];
}
if(num2!=num1)
k=0;
num2=0;
}
return k;
}
// 输出幻方
void print(int n)
{
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
cout<<a[i][j]<<"\t";
}
cout<<endl<<endl<<endl;
}
}
int main()
{
int n;
while(1)
{
cout<<"请输入你需要的幻方阶数,如果你想要结束请输入0:";
cin>>n;
if(n==0)
return 0;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
a[i][j]=0;
int num=n/2;
if(n%4!=0&&n%2==0)
{
//单偶幻方
change1(0,0,num-1,num-1,n/2,1);
change1(num,num,n-1,n-1,n/2,num*num+1);
change1(0,num,num-1,n-1,n/2,num*num*2+1);
change1(num,0,n-1,num-1,n/2,num*num*3+1);
change2(n);
}
else if(n%2==1)
{
//奇数阶幻方
change1(0,0,n-1,n-1,n,1);
}
//双偶幻方
else if(n%4==0)
{
two_even_numbers(n);
}
if(judge(n)==0)//判段幻方是否正确,如果正确输出
cout<<"error"<<endl;
else
print(n);
}
return 0;
}
参考:百度百科
























 2597
2597

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








