最优化方法（基于lingo）之 目标规划问题求解(6/6)

一、实验目的： 1. 练习建立实际问题的多目标规划模型。 2. 掌握用数学软件求解多目标规划的方法。 3. 实验从算法思想、实验步骤与程序、运行结果、结果分析与讨论等几方面完成。 4. 预习多目标规划的理论内容。

二、实验内容 题目： 建立模型并求解：某计算机公司生产3种型号的笔记本电脑A，B，C.这3种笔记本电脑需要在复杂的装配线上生产，生产1台A，B，C型号的笔记本电脑分别需要5，8，12(h).公司装配线正常的生产时间是每月1700h.公司营业部门估计A，B，C这3种笔记本电脑的利润分别是每台1000，1440，2520(元)，而公司预测这个月生产的笔记本电脑能够全部售出.公司经理考虑以下目标： 第一目标：充分利用正常的生产能力，避免开工不足. 第二目标：优先满足老客户的需求，A，B，C这3种型号的电脑50，50，80(台)，同时根据3种电脑的纯利润分配不同的权因子. 第三目标：限制装配线加班时间，不允许超过200h. 第四目标：满足各种型号电脑的销售目标，A，B，C型号分别为100，120，100(台)，再根据3种电脑的纯利润分配不同的权因子. 第五目标：装配线的加班时间尽可能少. 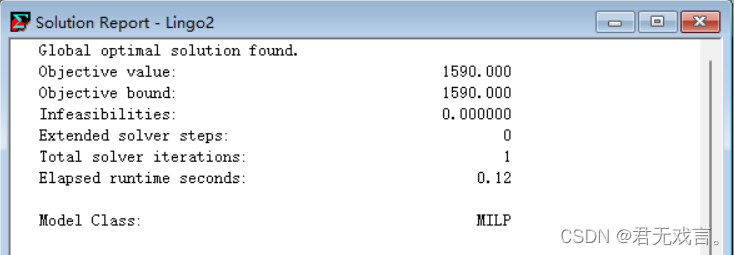数学模型：   程序代码： model:   sets:     vable/1..3/:x;     num/1..8/:g,a,b;     yueshu(num,vable):c;   endsets   data:     g=1700 50 50 80 100 120 100 1900;     c=5 8 12 1 0 0 0 1 0 0 0 1 1 0 0 0 1 0 0 0 1 5 8 12;   enddata   min=20*b(5)+18*b(6)+21*b(7);   @for(num(i):@sum(vable(j):c(i,j)*x(j))+b(i)-a(i)=g(i));   b(1)=0;   20*b(2)+18*b(3)+21*b(4)=0;   a(8)=0;   @for(vable:@gin(x)); end 程序执行结果： 结果解释： 由运行结果可知，x1=100,x2=55,x3=80，装配线生产时间为1900小时，满足装配线加班不超过 200小时的要求。能够满足老客户的需求，但未能达到销售目标。销售总利润为﹐100*1000+55*1440+80*2520=380800(元)。 题目：建立模型并求解：某化工厂拟生产两种新产品A和B，其生产设备费用分别为：A，2万元/吨；B,5万元/吨。这两张种产品均将造成环境污染，设由公害所造成的损失可折算为：A, 4万元/吨；B,1万元/吨。由于条件限制，工厂生产产品A和B的最大生产能力各为每月5吨和6吨，而市场需要这两张产品的产量每月不少于7吨。 试问工厂如何安排生产计划，在满足市场需要的前提下，使设备投资和公害损失均达最小。该工厂决策认为，这两个目标中环境污染应优先考虑，设备投资的目标值为20万元，公害损失的目标为12万元。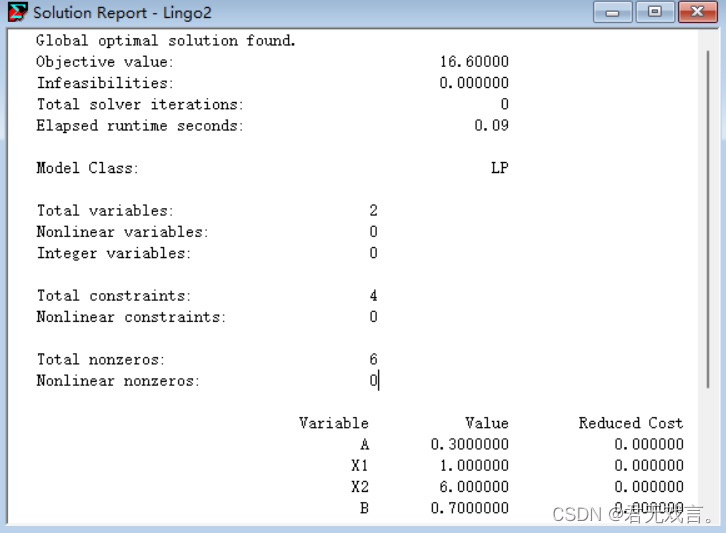 数学模型：环境污染优先考虑则将环境污染值权重赋 程序代码： model:   min=a*(2*x1+5*x2)+b*(4*x1+x2);   data:     a=0.3;     b=0.7;   enddata   x1<5;   x2<6;   x1+x2>7; end 程序执行结果： 结果解释： 得到x1=1,x2=6,满足总产量不少于7吨的要求，且均在生产能力范围内。此时所得收益为1*2+6*5=32万元/吨，到达了目标值，所造成的公害损失为1*4+6*1=10万元/吨，未超过目标值。

分析与讨论： 1.描述线性目标规划的单纯形法算法过程？ 具体算法过程如下： 将线性规划问题转化为标准形式：    - 最大化目标函数，即将目标函数的系数取相反数    - 所有约束条件转化为等式形式，引入人工变量和松弛变量    - 将约束条件与目标函数写成矩阵形式 初等变换将标准形式转换为初始单纯形：    - 以目标函数系数中最大的负数作为进入变量    - 以系数矩阵中最小非零元所在的行作为出去变量    - 对所有与出去变量有关的元素作初等行变换，使得出去变量成为单位向量    - 重复以上步骤，直到找到最优解或确定问题无解 通过单纯形算法改进单纯形：    - 在单纯形中选择离最优解最近的角点作为新的初始单纯形    - 逐步调整单纯形以找到更优的角点    - 重复以上步骤直到找到最优解 单纯形法结束：    - 如果目标函数的最大值/最小值等于0，则原问题有解且最优解为0    - 如果目标函数的最大值/最小值大于0/小于0，则原问题有/无解