3276.选择矩阵中单元格的最大值
给你一个由正整数构成的二维矩阵 grid。
你需要从矩阵中选择 一个或多个 单元格,选中的单元格应满足以下条件:
- 所选单元格中的任意两个单元格都不会处于矩阵的 同一行。
- 所选单元格的值 互不相同。
你的得分为所选单元格值的总和。
返回你能获得的 最大 得分。
示例
输入: grid = [[1,2,3],[4,3,2],[1,1,1]]
输出: 8
解释:
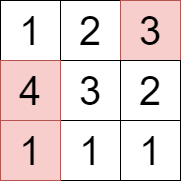
选择上图中用彩色标记的单元格,对应的值分别为 1、3 和 4 。
'''
值域状压DP
先找出整个二维数组的最大值
记录每个数值出现的行数
状态公式dp[i,j]表示将在[1,i]中选数目,目前已选的集合为[j],j为int,为位运算如1101表示{0,2,3}
状态转移方程为dp[i,j]=max(dp[i-1,j],dp[i-1,j|{tmp}]需要枚举当前i的所有tmp行)
时间复杂度为O(2^m*mn)
'''
class Solution:
def maxScore(self, grid: List[List[int]]) -> int:
mx=max(map(max,grid))
pos=[[] for i in range(mx+1)]
for i,row in enumerate(grid):
for tmp in row:
pos[tmp].append(i)
@cache
def dfs(i,j):
if i==0:
return 0
res=dfs(i-1,j)
for tmp in pos[i]:
if j>>tmp&1==0:
res=max(res,dfs(i-1,j|1<<tmp)+i)
return res
res=dfs(mx,0)
return res3277.查询子数组最大异或值
给你一个由 n 个整数组成的数组 nums,以及一个大小为 q 的二维整数数组 queries,其中 queries[i] = [li, ri]。
对于每一个查询,你需要找出 nums[li..ri] 中任意
子数组的最大异或值。
数组的异或值 需要对数组 a 反复执行以下操作,直到只剩一个元素,剩下的那个元素就是 异或值:
- 对于除最后一个下标以外的所有下标
i,同时将a[i]替换为a[i] XOR a[i + 1]。 - 移除数组的最后一个元素。
返回一个大小为 q 的数组 answer,其中 answer[i] 表示查询 i 的答案。
示例
输入: nums = [2,8,4,32,16,1], queries = [[0,2],[1,4],[0,5]]
输出: [12,60,60]
解释:
在第一个查询中,nums[0..2] 的子数组分别是 [2], [8], [4], [2, 8], [8, 4], 和 [2, 8, 4],它们的异或值分别为 2, 8, 4, 10, 12, 和 6。查询的答案是 12,所有异或值中的最大值。
在第二个查询中,nums[1..4] 的子数组中最大的异或值是子数组 nums[1..4] 的异或值,为 60。
在第三个查询中,nums[0..5] 的子数组中最大的异或值是子数组 nums[1..4] 的异或值,为 60。
'''
区间dp套区间dp
第一个dp[i][j]表示从i到j的异或值,状态转移方程为dp[i,j]=dp[i+1][j]^dp[i][j-1]
第二个mx[i][j]表示从i到j区间的最大异或值,状态转移方程为mx[i,j]=max(dp[i][j],mx[i+1,j],mx[i][j-1])
因为从下往上递推,从左往右递推,所以行数从n-1递推
列数从当前行数往右递推
'''
class Solution:
def maximumSubarrayXor(self, nums: List[int], queries: List[List[int]]) -> List[int]:
n=len(nums)
dp=[[0]*n for i in range(n)]
mx=[[0]*n for i in range(n)]
for i in range(n-1,-1,-1):
dp[i][i]=mx[i][i]=nums[i]
for j in range(i+1,n):
dp[i][j]=dp[i+1][j]^dp[i][j-1]
mx[i][j]=max(dp[i][j],mx[i+1][j],mx[i][j-1])
res=[]
for i in range(len(queries)):
res.append(mx[queries[i][0]][queries[i][1]])
return res思路图:
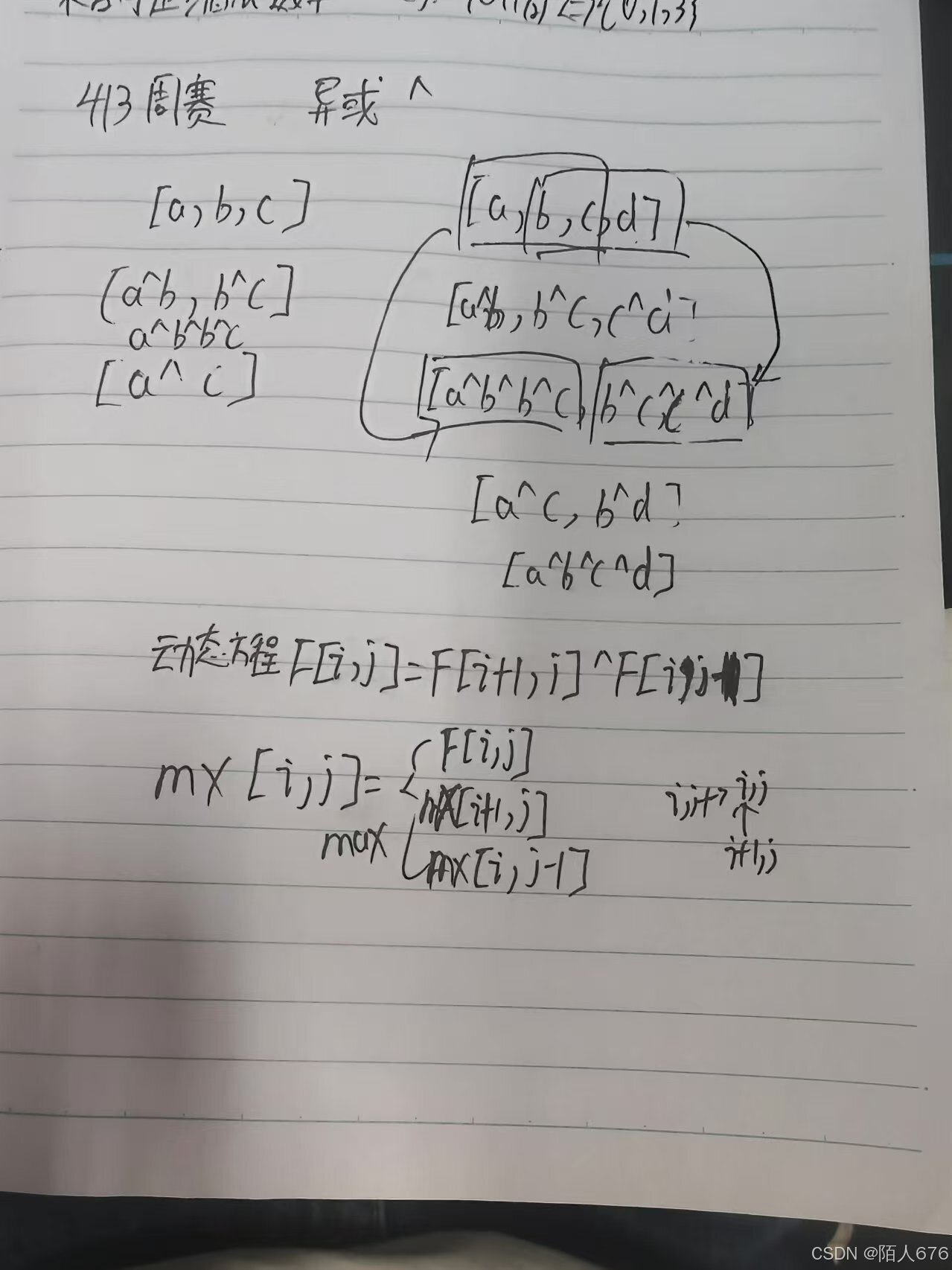























 16万+
16万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








