一、题目要求:
(一)输入:一个命题公式
(二)输出:1.真值表
2.主析取范式、主合取范式
3.给出命题公式的类别(永真、永假、可满足)
二、算法思想:
(一)顺序结构,循环处理;
(二)模块化思想,分为一个个函数;
(三)分级运算,合理处理!、/\、\/、=>、<=>五个运算。
三、算法表述:
对于输入的命题公式,主要以字符串的形式储存在数组当中,难点在于对于每一组变元的值按照命题公式的运算如何处理。
该算法分为,输入命题公式,打印真值表,运算处理,类别判断。
(一)输入命题公式:主要遍历字符数组,来判断命题变元的个数和命题公式的字符数;
(二)打印真值表:对于每一组变元的值,命题公式的字符数组需要进入运算处理函数进行运算,从而得到一组的值;
(三)运算处理:对于运算,优先级是一个难点;我将命题公式分为有括号和无括号的进行处理;首先,判断是否有括号,如果有,则找到最近的一对括号,进行运算,并对该对括号包括里面的所有字符进行标记;如果没有,则直接进入运算函数中。该运算函数利用顺序结构的特点,直接依次处理!、/\、\/、=>、<=>五个运算;
(四)类别判断:根据计算得出的0、1值进行判断,并以此得出主析取范式和主合取范式,进而判断该命题公式的类别。
四、流程图:

五、函数说明:
(一)变量定义:
全局变量:
char st[100],sttidai[100],x[50];//st存储输入的命题公式,sttidai复制st中的字符,x存储命题公式中的变量;
int stdata[100]={0};//对应st的整数型数组;
int b[50]={0};//b存储变量的值(0、1);
int n;//命题变元的个数;
int strl;//命题字符个数;
局部变量:
int t;//该命题的大,小项的个数;
t=pow(2,n);
int m[t]={0};//存储每一组变元的值对应的真值
int one=0,two=0;//one记录1的个数,two记录0的个数
(二)主函数:
int main()
{
print_title();//输入命题公式,并找出命题变元的个数;
int t;//该命题的大,小项的个数;
t=pow(2,n);
int m[t]={0};//存储每一组变元的值对应的真值
int one=0,two=0;//one记录1的个数,two记录0的个数
int i,j,k;
//打印真值表
for(i=0;i<n;i++)
{
printf("%c ",x[i]);
}
printf("\t%s\n",st);//第一行
for(j=0;j<t;j++)
{
strcpy(sttidai,st);//复制st的字符串 ,保留最初始的命题公式
for(i=0;i<n;i++)
{
printf("%d ",b[i]);
}
//求命题公式的值(0、1)
for(k=0;k<strl;k++)
digital(st[k],k);//给命题公式的对应变元,赋值
m[j]=print_zhenzhi();//计算该组变元的值所对应的真值
strcpy(st,sttidai);//将经改变的命题公式变回最初始的命题公式,进行下一轮的真值计算
printf("\t %d\n",m[j]);
if(m[j]==1)//记录真值为1的个数
one+=1;
else if(m[j]==0)//记录真值为0的个数
two+=1;
creat_zhenzhi(b,n-1);//创造下一组二进制数
}
leibie_judge(one,two,t,m);
return 0;
}
(三)输入命题公式:
void print_title()//输入命题公式, 并找出变元的个数n;
{
int i=0,j=0,k=0;//数组下标;
printf("请输入一个命题:\n");
scanf("%s",st);
while(st[i]!='\0')
{
int statu=1;//查找变元的标志数
if(st[i]!='('&&st[i]!=')'&&st[i]!='&'&&st[i]!='|'&&st[i]!='!'&&st[i]!='>'&&st[i]!='<')
{
for(k=0;k<j;k++)
{
if(st[i]==x[k])//判断st[i]是否和前几个变元有重复的
{
statu=0;//变元重复
break;
}
}
if(statu==1)//变元无重复
{
x[j]=st[i];
j++;
}
}
i++;
}
n=j;//变元的个数
strl=i;//命题公式的字符总数
}
(四)判断运算符:
int fei(int p)//!p; !代表非
{
int t;
t=!p;
return t;
}
int hequ(int p,int q)//p/\q; &代表合取
{
int t;
t=p&&q;
return t;
}
int xiqu(int p,int q)//p\/q; |代表析取
{
int t;
t=p||q;
return t;
}
int tiaojian(int p,int q)//p->q; >代表条件
{
int t;
t=(!p)||q;
return t;
}
int doubletiaojian(int p,int q)//p<->q; <代表双条件
{
int t;
t=((!p)||q)&&((!q)||p);
return t;
}
//判断运算符
int judge(int p,char ch,int q)
{
int t=0;
switch(ch)
{
case '&':
t=hequ(p,q);//合取
break;
case '|':
t=xiqu(p,q);//析取
break;
case '>':
t=tiaojian(p,q);//条件
break;
case '<':
t=doubletiaojian(p,q);//双条件
break;
}
return t;
}
(五)二进制生成器:
void creat_zhenzhi(int b[50],int n)//创造真值表的变元数据
{
int i;
i=n;
if(b[n]==0)//按二进制进行,该位为0,则变为1;
b[n]=1;
else // 该位为1,则变为0;继续进位
{
b[n]=0;
creat_zhenzhi(b,--i);
}
} //递归
//stdata中存储的真值
void digital(char ch,int t)
{
int i=0;
for(i=0;i<n;i++)
{
if(ch==x[i])
{
stdata[t]=b[i];//给对应的变元赋值(0、1)
break;
}
}
}
(六)分级运算:
//分级运算
int MAP(int k,int i)
{
int t;
int j;
int c;
for(j=k;j<i;j++)//处理非运算
{
if(st[j]=='!')
{
for(c=j+1;c<i;c++)
{
if(st[c]!='#')
{
t=fei(stdata[c]);
stdata[c]=t;
break;
}
}
}
}
for(j=k;j<i;j++)//处理合取
{
if(st[j]=='&')
{
for(c=j+1;c<i;c++)
{
if(st[c]!='!'&&st[c]!='#')
{
t=judge(stdata[j-1],st[j],stdata[c]);
stdata[c]=t;
break;
}
}
}
}
for(j=k;j<i;j++)//处理析取
{
if(st[j]=='|')
{
for(c=j+1;c<i;c++)
{
if(st[c]!='!'&&st[c]!='&'&&st[c]!='#')
{
t=judge(stdata[j-1],st[j],stdata[c]);
stdata[c]=t;
break;
}
}
}
}
for(j=k;j<i;j++)//处理条件
{
if(st[j]=='>')
{
for(c=j+1;c<i;c++)
{
if(st[c]!='!'&&st[c]!='&'&&st[c]!='|'&&st[c]!='#')
{
t=judge(stdata[j-1],st[j],stdata[c]);
stdata[c]=t;
break;
}
}
}
}
for(j=k;j<i;j++)//处理双条件
{
if(st[j]=='<')
{
for(c=j+1;c<i;c++)
{
if(st[c]!='!'&&st[c]!='&'&&st[c]!='|'&&st[c]!='>'&&st[c]!='#')
{
t=judge(stdata[j-1],st[j],stdata[c]);
stdata[c]=t;
break;
}
}
}
}
return t;//返回对于一组变元,经运算后的真值
}
(七)运算处理(有括号、无括号):
//判断是否有括号
int kuohao()
{
for(int i=0;st[i]!='\0';i++)
{
if(st[i]=='('||st[i]==')')
return 1;
}
return 0;
}
//st命题公式,x变元,b变元的真值,n变元个数; st、x、b均从下标0开始;
int print_zhenzhi()//求命题的真值;
{
int t=0;
int k=0;
int i,j;
if(kuohao())//有括号的运算
{
for(i=0;st[i]!='\0';i++)
{
if(st[i]==')')//找到最近的一个右括号
{
for(j=i-1;;j--)
{
if(st[j]=='(')//找到左括号的位置
{
break;
}
}
k=j+1;
stdata[i]=MAP(k,i);//进入无括号的命题公式的运算 ,并将运算结果赋给右括号位置的数
for(j=k-1;j<i;j++)
{
st[j]='#';
}
st[i]='*';//将此内括号的所有字符做标记
}
}
}
if(kuohao()==0)//无括号的运算
stdata[i-1]=MAP(0,strl);
return stdata[i-1];//返回该组变元值所对应的真值
}
(八)判断类别,给出主析取、合取范式:
void leibie_judge(int one,int two,int t,int m[])
{
int yi=0,er=0;
int j;
if(one==0)//真值表中无真值1的结果
printf("无主析取范式\n该式为永假式\n");
else if(one>0)
{
printf("主析取范式为:\n");
for(j=0;j<t;j++)
{
if(m[j]==1)
{
printf("m(%d)",j);
yi++;
if(yi<one)
printf("\\\/");
}
}
printf("\n");
}
if(two==0)//真值表中无真值0的结果
printf("无主合取范式\n该式为永真式\n");
else if(two>0)
{
printf("主合取范式为:\n");
for(j=0;j<t;j++)
{
if(m[j]==0)
{
printf("M(%d)",j);
er++;
if(er<two)
printf("\/\\");
}
}
printf("\n");
}
if(one>0&&two>0)
printf("该式为可满足式\n");
}
六、运行截图:
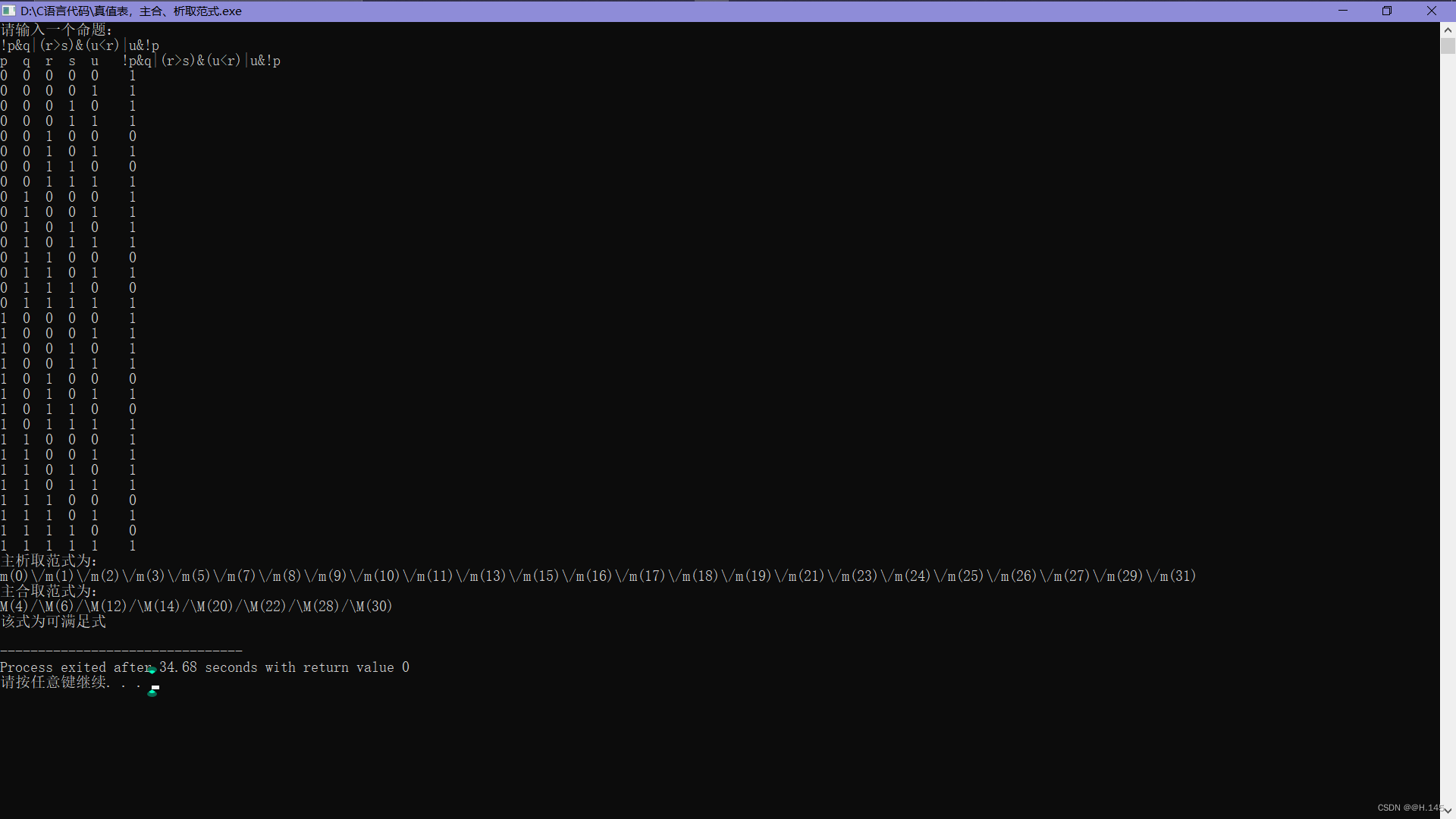

七、学习感受:
(一)下次要搞清楚栈,用栈尝试一下;
(二)一定记得有的变量需要每次初始化;
(三)模块化很重要,有利于设计算法,更简单。


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








