“数字大冒险：探索二分查找的神奇之旅“

最新推荐文章于 2025-05-07 10:28:42 发布

小蜗牛~向前冲

最新推荐文章于 2025-05-07 10:28:42 发布

阅读量1.1k

点赞数 59

分类专栏：小蜗牛算法之路文章标签： leetcode 算法职场和发展

本文链接：https://blog.csdn.net/qq_61552595/article/details/137560585

版权

小蜗牛算法之路专栏收录该内容

5 篇文章

订阅专栏

本文详细介绍了二分查找的基本概念、朴素模板的实现以及如何扩展到万能模板，包括查找目标值、区间左右端点定位，同时强调了处理边界情况和细节的重要性，适用于IT技术中数组操作和高效搜索算法的学习。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前言

作者：小蜗牛向前冲

专栏：小蜗牛算法之路

专栏介绍："蜗牛之道，攀登大厂高峰，让我们携手学习算法。在这个专栏中，将涵盖动态规划、贪心算法、回溯等高阶技巧，不定期为你奉上基础数据结构的精彩算法之旅。一同努力，追逐技术的星辰大海。"

一、二分查找

二分查找是一种在有序数组中查找目标值的算法。它通过反复将待查找区间分成两部分并检查中间元素来进行查找，以缩小搜索范围，直到找到目标值或确定目标值不存在为止。这种算法的时间复杂度为 O(log n)，其中 n 是数组的元素个数。

对于二分查找，我们简单的理解就是通过二段性，不断的排除不属于目标值的的算法。

而为什么我们不三分，四分呢？

尽管三分、四分等算法在某些特定情况下可能会有所优势，但由于二分查找已经被广泛证明为高效且简单的解决方案，因此通常情况下选择二分更为合适。（这里和数学期望有关就不和大家证明了）

二分算法看起来非常简单，但是他的细节是非常多，而且查看能力非常强大。

比如当我们要查找2^32（42亿多）,如果我们要暴力查找就要查找42亿多次，但是二次就只要查找32次。

为了解决二分细节太多问题(特别是在处理复杂问题，对边界情况的处理）

二、二分的朴素模板

1、例题1

这里我们直接用力扣上的一道题目来引出：

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
提示：

你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。

这里是非常经典的二分运用，在一个有序的数组中（有序就说明有二段性） ，让我们排查目标值target,暴力就不提了，那二分是如何解题的。

这时候结果区域就只剩5、9、12,然后继续二分排除。

这里就不在细说，直接看代码。

class Solution {
public:
    int search(vector<int>& nums, int target)
    {
        int left = 0;
        int right = nums.size()-1;
        while(left<=right)
        {
            int mid =(left+right)/2;
            if(nums[mid]<target)
            {
                left = mid+1;
            }
            else if(nums[mid]>target)
            {
                right = mid-1;
            }
            else
            {
                return mid;
            }
        }
        return -1;
    }
};

通过这道题目我们来总结一下朴素模板。

2、朴素模板

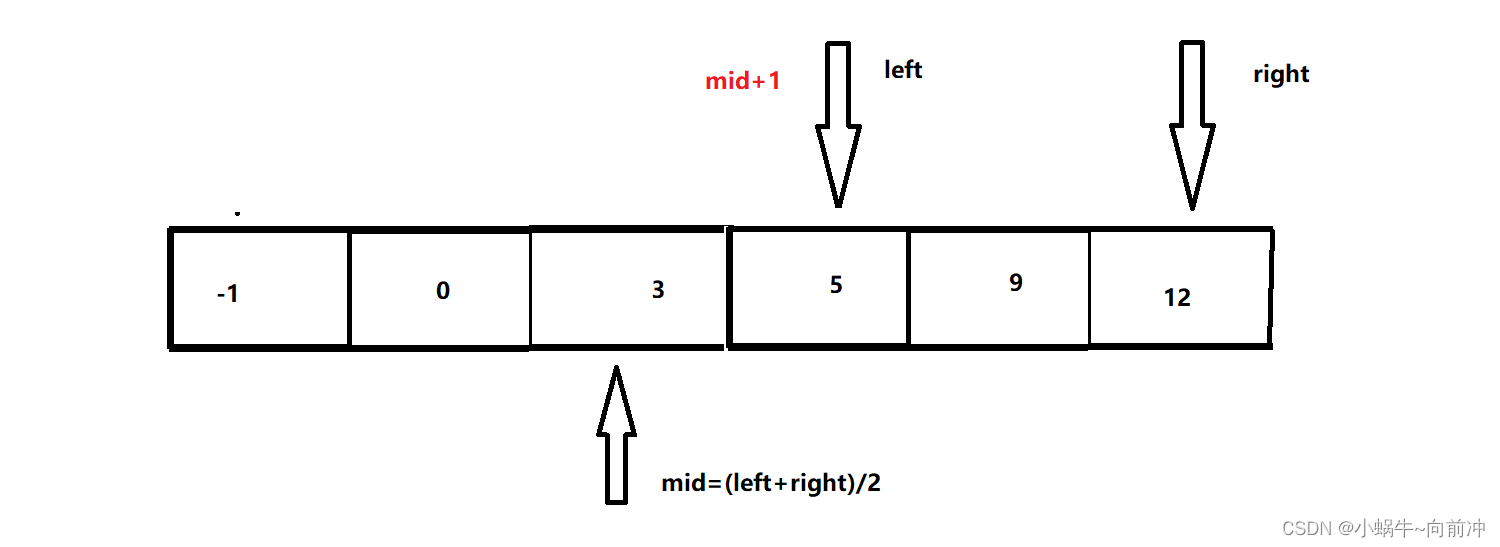
这里简单说明一下，x=nums[mid],t为目标值。

这里为了保证left<=right

当x < t----->left =mid+1------[left,right]
当x > t----->right =mid-1------[left,right]
当x == t----->返回结果

从上面我们可以归纳出二分的朴素模版：

  while (left <= right)
  {
      int mid = left + (right-left)/2;//防止溢出
      if (....)
      {
          left = mid + 1;
      }
      else if (.....)
      {
          right = mid - 1;
      }
      else
      {
          .....;
      }
  }

细节处理

1、循环结束的条件 left<right可不可以

这里是一定不可以的，这里会漏掉，当left和right都指向同一个元素的情况，大家注意在[left,right]区间的值都是没有被排查的，所以条件一定是lef<=right。

2、在计算mid的时候有时候我们会看到二种写法：

int mid = left + (right-left)/2;
int mid = left + (right-left+1)/2;

对于二者的区别其实对奇数个元素是没有区别的，因为中间值一定是唯一的。

但是对于偶数个元素的，中间值mid就有区别了：

可以看到mid 是第一种求法的时候取到是方框中左边的值，第二中求法求到是右边的值。

对于这中朴素模板来说是没有区别的，但是对后面的万能模版来说却非常重要。

三、二分的万能模版

1、例题2

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1：
输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]
示例 2：
输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]
示例 3：
输入：nums = [], target = 0
输出：[-1,-1]
提示：

0 <= nums.length <= 105
-109 <= nums[i] <= 109
nums 是一个非递减数组
-109 <= target <= 109

对于这道例题，如果我们继续用前面的朴素二分算法模本版，就要处理许多边界问题，那么我们应该如何求简化我们的思路。

2、查找区间左端点

为了解决上面朴素二分在求上面情况，可能会出现退化为暴力的情况，这里我们换一个思路，利用二分求我们要求区间的左端点。

这里我们就分为了上面二种情况，但是仅仅到这里我们就可以求编写代码了吗？我觉的是远远不够，因为对于二分来说，最复制的是其中的边界问题，没有处理好就会出现一系列的死循环问题。

细节处理

循环条件：

left<right?
left<=right?

这里的循环条件是1还是2,这里我们先说结论，一定不能取等号(所以选择情况1)。为什么？

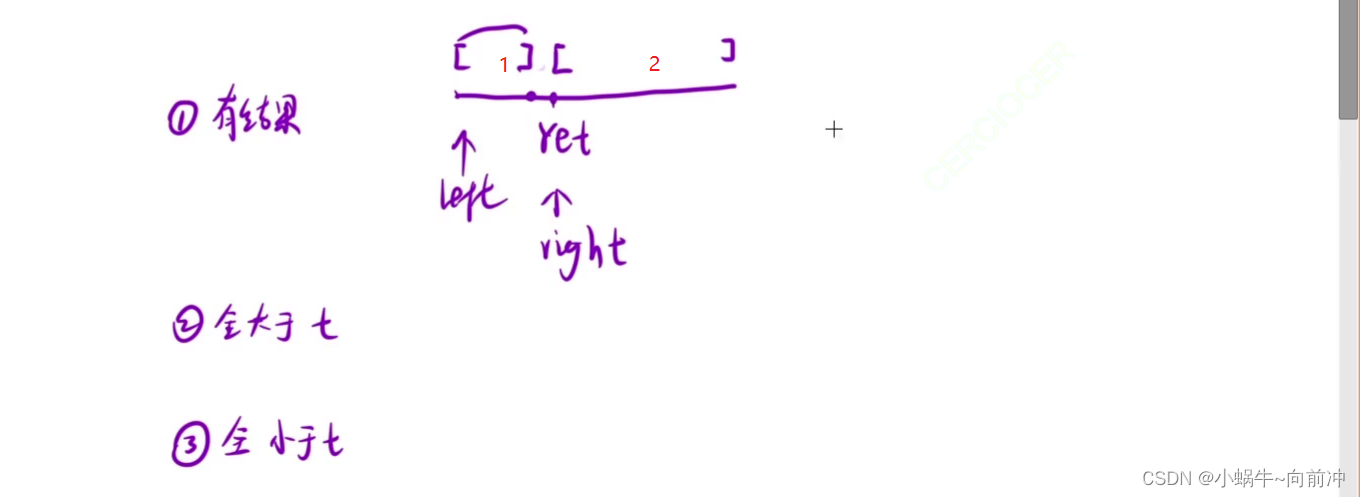对于情况1：

当我们要查看的是有结果的，也就是说在[left，right]区间内，存在我们要的结果(左区间端点)

对于left,一直是想要跳出1这个区域的，但是对于right就会在2区域内活动，当left==right=r=et,就是等于了结果，也就没有必要在进入循环(如果进行就会死循环，因为mid=right)。

对于情况2：

在想x>t,那么right就要一直向左移动，最终就会和left相遇，这里就只要判断当前值是否和t相等即可，没有必要进入循环（如果进入就会出现死循环）

对于情况3：

在想x<t,那么left就要一直向右移动，最终就会和right相遇，这里就只要判断当前值是否和t相等即可，没有必要进入循环（如果进入就会出现死循环）

综合上所述：

left==right的时候就是最终结果，没有必要进入循环判断
如果判断就会死循环

2、求mid的操作

int mid = left + (right-left)/2;
int mid = left + (right-left+1)/2;

这里也是选择1 ,为什么？

当最后只有二个值的时候，如果我们选择2求mid，可以想一下，mid就会指选择区域右边(前面已经解释过了)，当是如果是x<=t的情况时候，这时候就会出现right=mid，[left,right]区间没有动而出现死循环。

而现在1就不会出现这种情况

代码实现：

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target)
    {

        int left = 0;
        int right = nums.size()-1;
         vector<int> result = {-1, -1};
        if(nums.size()==0) return result;//处理边界情况
        while(left<right)
        {
            int mid =left+(right-left)/2;
            if(nums[mid]<target)
            {
                left = mid+1;
            }
            else
            {
                right = mid;
            }
        }
        //得到左区间的的下标,这里出来一定是left==right
        int begin=-1,end=-1;
        if(nums[left]==target)
        {
            begin = left;
            int i = 0;
            //从left位置开始找右区间
            for(i = left;i<nums.size();i++)
            {
                if(nums[i]!=target)break;
            }
            end = i-1;
            result[0]=begin;
            result[1]=end;
        }
        return result;
    }
};

3、查找区间右端点

对于找区间右端点，和找左端点的本质上是一样的，只是变了一种形式，下面我们快速了解一下：

这里不同点：就是区间划分不一样了，因为是找右端点，所以当x<=t时候，left在移动的时候，不能超过区间，所以最多到left=mid这的区间是，当x>t的时候，其实是和朴素二分哪里right的移动是一样的。

对于查找区间右端点我们仍要关注二个细节：

循环结束条件是：left<rigt
mid的求法是:left+(right-left+1)

这里至于是为什么，可以参考区间左端点细节的解释，这里就不过多解释。

代码实现：

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) 
    {
        vector<int> result{-1,-1};
        int left=0,right = nums.size()-1;
        //处理特殊情况
        if(nums.size()==0) return result;
        while(left<right)
        {
            int mid= left+(right-left+1)/2;
            if(nums[mid]<=target) left=mid;
            else right = mid-1;
        }
        //到这里肯定是left==right
        int begin =-1,end=-1,i=0;
        if(nums[left]==target)
        {
            end = left;
            //在去找左端点
            for(i = left;i>=0;i--)
            {
                if(nums[i]!=target)break;
            }
            begin = i+1;
        }
        result[0]=begin;
        result[1]=end;
    return result;
    }
};