第六届“传智杯”全国大学生计算机大赛复赛B组（A-E）题解

已于 2023-12-22 14:35:16 修改
阅读量979 收藏 7
点赞数 4
文章标签： 算法 c++ 数据结构
于 2023-12-22 01:45:48 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_61637732/article/details/135128551
版权
文章讲述了小红遇到的几个编程问题，包括字符串分割、数字分裂（寻找最大公因数），字符串同构判断，树上赋值方案（满足红色节点权值和为3的倍数），以及区间查询操作。涉及到的算法有字符串处理、数学运算和数据结构如树形dp和线段树。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

A-小红劈字符串

题目描述

小红拿到了一个字符串，她准备把这个字符串劈成两部分，使得第一部分的长度恰好是第二部分的两倍。你能帮帮她吗？

输入格式

一个仅由小写字母组成的字符串，长度不超过10^{5}

输出格式

无解输出-1

有解则输出两个劈好了的字符串

题解

先看字符串长度是否为3的倍数，然后先输出前2/3的长度，在输出后面的部分就好了

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#include<cmath>
#include<vector>
#include<set>
using namespace std;
const int N=2e5+5;

int main()
{
	std::ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    string s;
    cin>>s;
    int len=s.length();
    if(len%3)
    {
    	cout<<-1;
    	return 0;
	}
	for(int i=0;i<len/3*2;i++)
	cout<<s[i];
	cout<<' '; 
	for(int i=len/3*2;i<len;i++)
	cout<<s[i];
}

B-小红的数字分裂

题目描述

小红有一个数组，她每次可以选择数组的一个元素 x ，将这个元素分成两个元素 a 和 b ，使得 

x=a+b

请问小红最少需要操作多少次才可以使得数组的所有元素都相等。

输入格式

第一行一个整数n,其中1\leqslant n\leqslant10 ^{5}，表示数组长度

第二行输入n个整数表示数组(1\leqslant a_{i}\leqslant 10 ^{9})

输出格式

输出一个整数表示答案。

题解

要把所有的数都分解成相同的数，那么最后的数应该是数组中所有数的公因数

又因为所有要求操作次数最小，所以应该是去找最大公因数，假设该最大公因数是g

那么a_{i}对答案的贡献应该等于\frac{a_{i}}{g}-1

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#include<cmath>
#include<vector>
#include<set>
using namespace std;
const int N=2e5+5;
typedef long long ll;
typedef pair<int,int> PII;

ll a[N];

int main()
{
	std::ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    int n;
    cin>>n;
    ll g=0;
    ll ans=0;
    for(int i=1;i<=n;i++)
    {
    	cin>>a[i];
    	g=__gcd(g,a[i]);
	}
	for(int i=1;i<=n;i++)
	{
		ans+=(a[i]/g)-1;
	}
	cout<<ans;
}

C-小红的字符串同构

题目描述

小红定义两个字符串同构，当且仅当对于 i∈[1,n ], b[i]−a[i] i∈[1,n], b[i]-a[i] i∈[1,n],b[i]−a[i]是定值。例如，"bacd"和"edfg"是同构的。

现在小红拿到了一个长度为n的字符串a，她想知道，有多少长度为n的字符b同时满足以下两个条件：
1.b的每一位都和a不同。
2.b和a不同构。

输入格式

一个仅由小写字母组成的，长度不超过10^{5}的字符串a

输出格式

一个整数表示答案，对1e9+7取模

题解1

首先来理解一下题目描述的 “同构” ,也就是说两个字符串长度相等，并且每个字符之间的 “位移”是相等的（注意，这里的位移是有正负的），举个例子：cd 与 ab 同构，但 cd 不与 af 同构，因为'c' - 'a'= - 2,'d' - 'f' = 2

这里提供一个O(26*N)的做法:

假设字符串长度为len

首先，枚举合法的字符串b的第一位是哪个字母，这样我们能确定位移d(d ! = 0)

然后，遍历2-len位

我们首先判断 a[i]+d是否还是小写字母

若不是小写字母，则一定不会构成同构,后面每一位都能选25个字母，遍历终止

计算答案

ans=(ans+POW(25,1ll*(s.size()-j)))%P;

若还是小写字母，则1-i位可能构成同构

此时我们再分类讨论：

1.若不选该字母，则不可能构成同构，当前位可选24个字母，后面每一位可选25个字母

计算答案

ans=(ans+(24*POW(25,1ll*(s.size()-j-1)))%P)%P;

2.选择该字母，则1-i位是同构的，观察下一位

代码

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#include<cmath>
#include<vector>
#include<set>
using namespace std;
const int N=2e5+5;
typedef long long ll;
typedef pair<int,int> PII;
int e[N],ne[N],h[N],idx;
ll finv[N],fac[N];
ll P=1e9+7;
ll POW(ll x,int k=P-2,ll rs=1){while(k){if(k&1)rs=rs*x%P;x=x*x%P;k>>=1;}return rs;}

int main()
{
	std::ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    string s;
    cin>>s;
    ll ans=0;
    //枚举第一位可选哪个字母 
    for(int i='a';i<='z';i++)
    {
    	//d!=0
    	if(s[0]==i)
    	{
    		continue;
		}
		int d=i-s[0];
		for(int j=1;j<s.size();j++)
		{

			int now=s[j]+d;
			//若前j位可以构成同构，则当前位填其余24个字母之后，(0到j-1位都是同构的)后面每一位都能填25个字母，计算一次答案 
			//若当前位填now，（0-j位都是同构的），观察下一位，继续循环 
			if(now>='a' && now<='z')
			{
				ans=(ans+(24*POW(25,1ll*(s.size()-j-1)))%P)%P;
			}
			//如果此时一定不能构成同构，则j位到最后一位都能填25个字母，计算答案，循环终止 
			else
			{
				ans=(ans+POW(25,1ll*(s.size()-j)))%P;
				break;
			}
			
		}
	}
	cout<<ans;
}

这也是愚钝的博主最开始想出来的做法，下面来介绍官方的O（N）的做法

题解2

首先计算满足 条件1 的字符串的个数，答案为25^{n}

而同构的字符串数量也能直接计算出来，答案为26-（最大的字符-最小的字符+1）

如何来理解这个同构的字符串数量的计算？

举个例子，如图，假设字符串a中最小的字符是 'c'，最大的是 'w'，因为a字符串中的每个字符都要进行 “移动”，且不能超过小写字母的范围，假设  ' w ' 变成 ' t '，那么' c '变成' a ' 之后还要再往前移动，所以超过了小写字母范围，对 'w',来说同理，所以同构字符串的数量等于图中绿线可移动的范围

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll mod=1e9+7;
signed main(){
    string s;
    cin>>s;
    int ma=0,mi=1e9;
    ll res=1;
    for(auto i:s){
        ma=max(ma,(int)(i-'a'));
        mi=min(mi,(int)(i-'a'));
        res=res*25%mod;
    }
    cout<<res-(26-(ma-mi+1));
    
}

D-小红的树上赋值方案

题目描述

小红拿到了一棵有根树，其中有一些节点被染成了红色。树的根节点是 1 号节点。
小红希望你给每个节点的权值赋值为 1 或者 2，需要满足每个红色节点的子树节点权值之和为 3 的倍数。
请你帮小红求出赋值的合法方案数。由于答案可能过大，请对1e9+7取模

输入格式

第一行输入一个正整数n，代表节点的数量。
第二行输入一个长度为n的字符串，第i个字符为'R'代表i号节点被染成红色，为'W'代表未被染色。
第三行输入n−1个正整数ai​，第i个正整数代表i+1号节点的父亲编号。
1\leq n\leq 10^{5}

输出格式

一个整数代表答案

题解

官方题解是树形dp，很好理解，这里给出博主赛时想到的做法

首先考虑，一颗根被染成了红色，且其他根没有被染色的大小为size的树的答案

那么这个树的所有节点权值和value满足size\leqslant value\leqslant 2*size

假设所有节点权值为1，value=size,为2，value=2*size

那么我们假设树中所有节点权值都为1，然后枚举权值从1变成2的节点个数，若总和为3的倍数，我们用组合数计算一次答案

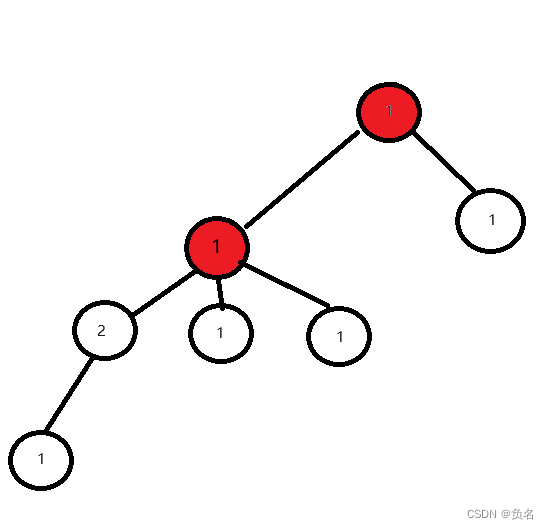
举个例子：

这里的size=5,那当权值为2的节点个数是1,4的时候可以满足题意

那么这颗 “红根树”的答案就是C_{5}^{1}+C_{5}^{4}

这是根被染成红色时的答案

那么对于原来的题意应该怎么做呢？

其实我们可以发现，如果一颗根是红色的树有红根子树，那么我们就不需要考虑它了，因为这颗树的方案已经被计算出来了，那就把这个红根子树的size当作0就好了，然后答案还要累乘上当前红根树的贡献

这里的答案就是(C_{5}^{1}+C_{5}^{4}) * C_{2}^{1}

最后来考虑一些特殊情况：

1.如果树上没有红色的节点，那么每个节点都能填1或2，答案就是2^{size}

2.如果一颗根是红色的树的size=1，那么最后的答案应该是0

想清楚之后我们就能写代码了

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#include<cmath>
#include<vector>
#include<set>
using namespace std;
const int N=1e5+5,M=2*N;
typedef long long ll;
typedef pair<int,int> PII;
int e[M],ne[M],h[N],idx;
ll finv[N],fac[N];
ll P=1e9+7;
ll POW(ll x,int k=P-2,ll rs=1){while(k){if(k&1)rs=rs*x%P;x=x*x%P;k>>=1;}return rs;}
void init()
{
    finv[1]=finv[0]=fac[0]=1;
    for(int i=1;i<N;++i)fac[i]=fac[i-1]*i%P;
    finv[N-1]=POW(fac[N-1]);
    for(int i=N-2;i;--i)finv[i]=finv[i+1]*(i+1)%P;
}
ll C(int a,int b)
{
    if(b>a||a<0||b<0)return 0;
    return fac[a]*finv[a-b]%P*finv[b]%P;
}
void add(int a,int b)
{
	e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

char color[N];
int sz[N];
ll ans=1;
void dfs1(int x,int fa)
{
	sz[x]=1;
	for(int i=h[x];~i;i=ne[i])
	{
		int j=e[i];
		if(j==fa) continue;
		dfs1(j,x);
        
        //不计算红色子树的size
		if(color[j]=='R')
		continue;
		sz[x]+=sz[j];
	}
}

void dfs2(int x,int fa)
{
	if(color[x]=='R')
	{
		ll cal=0;
		for(int i=0;i<=sz[x];i++)
		{
			if((sz[x]+i)%3==0)
			{
				cal=(cal+C(sz[x],i))%P;
			}
		}
//		cout<<"cal="<<cal<<endl;
		ans=(ans*cal)%P;
	}
	for(int i=h[x];~i;i=ne[i])
	{
		int j=e[i];
		if(j==fa) continue;
		dfs2(j,x);
	}
}

int main()
{
	std::ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    //初始化求组合数的部分
    init();
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
    	cin>>color[i];
    	if(color[i]=='R')
    	h[i]=-1;
	}

    int fa;
    for(int i=2;i<=n;i++)
    {
    	cin>>fa;
    	add(fa,i),add(i,fa);
	}
    //dfs1求出每颗红根树的size
	dfs1(1,0);
	dfs2(1,0);
    
    /*
    如果1号根节点没有被染色
    那么答案还要乘上2的根节点size的幂次
    */
    if(color[1]=='W')
    {
    	ans=(ans*POW(2,sz[1]))%P; 
	}
	cout<<ans;
}

E-小红的区间查询

题目描述

小红拿到了一个几何，初始为空集。小红可以进行下面两种操作：

+ l r  ：将区间(l,r)添加进集合

- l r ： 将区间(l,r)从集合中删除

删除时保证一定能删除

问每次操作之后是否存在两个区间相交

输入格式

第一行输入一个正整数q,代表操作次数

接下来q行输出一个字符op与两个正整数l,r，代表操作

1\leq q\leq 10^{5}

1\leq l\leq r\leq 10^{9}

输出格式

存在输出"Yes",不存在输出"No"

题解

很容易想到直接用线段树维护区间加，每次操作后查询区间最大值是否>1即可

由于l,r范围很大，但是q的次数很小，所以我们可以先进行离散化处理

这里附上一份官方代码

#include <bits/stdc++.h>

using ll = long long;

template<class Info, class Tag, class Merge = std::plus<Info>>

class LazySegmentTree {
private:
    int n;
    const Merge merge{};
    std::vector<Info> info;  // data of segment tree, 1-index
    std::vector<Tag> tag;  // lazy tag of segment tree

    /* [x, y) and val: Add val to each element in range of [x, y)
     * p: The id of subtree, which is an index of vector 'info'.
     * [l, r): The range of p.
     */
    void innerPull(int p) {
        info[p] = merge(info[p << 1], info[p << 1 | 1]);
    }
    void innerApply(int p, const Tag &v, int l, int r) {
        // TODO: update the apply function
        auto applyInfo = [&](Info &a, const Tag &b, int l, int r) {
            a.min += b;
            a.max += b;
        };
        auto applyTag = [&](Tag &a, const Tag &b, int l, int r) {
            a += b;
        };
        applyInfo(info[p], v, l, r);
        applyTag(tag[p], v, l, r);
    }
    void push(int p, int l, int r) {
        if (tag[p] != Tag()) {
            int m = (l + r) / 2;
            innerApply(p << 1, tag[p], l, m);
            innerApply(p << 1 | 1, tag[p], m, r);
            tag[p] = Tag();
        }
    }
    void update_(int p, int x, int y, const Tag &v, int l, int r) {
        if (x <= l && r <= y) {
            innerApply(p, v, l, r);
            return;
        }
        int m = (l + r) / 2;
        push(p, l, r);
        if (x < m) update_(p << 1, x, y, v, l, m);
        if (y > m) update_(p << 1 | 1, x, y, v, m, r);
        innerPull(p);
    }
    /* Query the sum-up value of range [x, y). */
    Info query_(int p, int x, int y, int l, int r) {
        if (x <= l && r <= y) return info[p];
        if (x >= r || y <= l) return Info();
        int m = (l + r) / 2;
        push(p, l, r);
        return merge(query_(p << 1, x, y, l, m), query_(p << 1 | 1, x, y, m, r));
    }

public:
    LazySegmentTree(int n = 0) { init(n); }
    LazySegmentTree(std::vector<Info> &init) : LazySegmentTree(init.size()) {
        std::function<void(int, int, int)> build_ = [&](int p, int l, int r) {
            if (r - l == 1) {
                info[p] = init[l];
                return;
            }
            int m = (l + r) / 2;
            build_(p << 1, l, m);
            build_(p << 1 | 1, m, r);
            innerPull(p);
        };
        build_(1, 0, n);
    }
    void init(int n) {
        this->n = n;
        info.assign(4 << std::__lg(n), Info(0, 0));
        // info.resize(4 << std::__lg(n));
        tag.resize(4 << std::__lg(n));
    }
    /* Add val to each element in range of [x, y) */
    void update(int x, int y, Tag v) {
        update_(1, x, y, v, 0, n);
    }
    /* Query the sum-up value of range [x, y) */
    Info query(int x, int y) {
        return query_(1, x, y, 0, n); 
    }
};

struct MinMax {
    static constexpr int inf = 1e9;
    int min, max;
    MinMax(int min = inf, int max = -inf) : min(min), max(max) {}
    MinMax operator+(const MinMax &rhs) const {
        return MinMax(std::min(min, rhs.min), std::max(max, rhs.max));
    }
    MinMax &operator+=(const MinMax &rhs) {
        return *this = *this + rhs;
    }
};

int main() {
    std::ios::sync_with_stdio(false);
    std::cin.tie(nullptr);

    int m;
    std::cin >> m;
    std::set<std::pair<int, int>> st;
    std::vector<std::tuple<char, int, int>> ops;
    while (m--) {
        char op;
        int l, r;
        std::cin >> op >> l >> r;
        ops.emplace_back(op, l, r);

        if (op == '+') {
            assert(st.find(std::pair(l, r)) == st.end());
            st.emplace(l, r);
        } else {
            assert(st.find(std::pair(l, r)) != st.end());
            st.erase(std::pair(l, r));
        }
        
    }

    std::vector<int> a;
    for (auto [op, l, r] : ops) {
        a.push_back(l);
        a.push_back(r);
    }

    std::sort(a.begin(), a.end());
    a.erase(std::unique(a.begin(), a.end()), a.end());
    for (auto &[op, l, r] : ops) {
        l = std::lower_bound(a.begin(), a.end(), l) - a.begin();
        r = std::lower_bound(a.begin(), a.end(), r) - a.begin();
    }

    LazySegmentTree<MinMax, int> seg(a.size());
    for (auto [op, l, r] : ops) {
        if (op == '+') {
            seg.update(l, r, 1);
        } else {
            seg.update(l, r, -1);
        }
        if (auto [min, max] = seg.query(0, a.size()); min < 0 || max > 1) {
            std::cout << "Yes\n";
        } else {
            std::cout << "No\n";
        }
    }

    return 0;
}

负名
关注
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值