人群计数densitymap生成简述及python实现代码

本文链接：https://blog.csdn.net/qq_61676281/article/details/131845706

本文详细介绍了基于MCNN的密度图生成方法，包括数据集分析、密度函数表示、高斯核函数的应用以及代码实现。通过使用高斯核函数对人头标注进行加权，可以生成反映人群密度的图像。提供的Python代码展示了固定参数和几何自适应核两种方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

概述

本文主要以个人学习的顺序复现了MCNN（ Multi-column Convolutional Neural Network ）中提出的生成密度图的方法。

数据集分析

本文使用的数据集shanghaiTech由原始图片和标注文件共同构成，该数据集包含part_A_final，part_B_final两部分。

以 part_A_final为例，包含了test data与train data，两者不重复，组成形式相同。其中，images为原始图片，ground_truth标注文件是mat格式，里面记录了每个注释人头的二维坐标和总人头数量。

密度图生成原理

1.密度函数表示

如果在像素xi处存在头部，我们将其表示为delta函数δ（x − xi）。因此，具有标记的N个头部的图像可以表示为函数

补充delta函数定义：

通俗来理解，H（x）为与原始图像大小相同的矩阵，当位置xi处有一个人头时，矩阵中该位置的点置为1，其余为0。

2.高斯核函数与参数确定

对于给定图像中的每个头部xi，我们将到其k个最近邻居的距离表示为{di 1，di 2，...，di m}。因此平均距离为d¯ i = 1/ m ∑ di j。因此，与xi相关联的像素对应于场景中地面上的区域，该区域的半径大致与di成比例。因此，为了估计像素xi周围的人群密度，我们需要将δ（x-xi）与方差σi与¯di成比例的高斯核卷积。

本问题需要使用到的二位高斯核函数：

3.为什么使用高斯核函数？

高斯核的函数图像是一个正态分布钟形线，坐标越趋近中心点，值就越大，反之越小。也就是说离中心点越近权值就越大，离中心点越远，权值就越小。

举例：

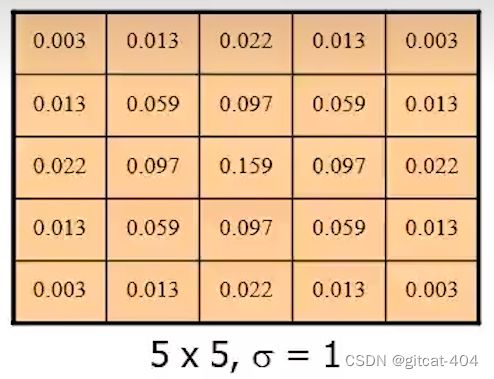
对中心点使用高斯核函数后，周围像素点的权值相加起来等于1；这样既不影响生成的密度图中总人头数，又能够比较真实的反应每个人头在空间里面的位置特征。

代码实现

固定参数核python代码复现：

#固定参数核
import numpy as np
from scipy.ndimage import gaussian_filter

def compute_density_map(im, points):
    #根据图片大小生成全0矩阵
    h, w = im.shape[:2]
    im_density = np.zeros((h, w))
    
    #如果坐标点个数即人头数为1，则将该点对应的像素位置设置为最大值255，并返回
    if len(points) == 1:
        x1 = max(1, min(w, round(points[0, 0])))
        y1 = max(1, min(h, round(points[0, 1])))
        im_density[y1, x1] = 255
        return im_density
    #对每个标注点开始遍历
    #定义一个高斯窗口的尺寸(f_sz)和标准差(sigma)，并使用fspecial函数创建一个高斯滤波器(H)
    for point in points:
        f_sz = 15
        sigma = 4.0
    #生成高斯核
        H = gaussian_filter(np.zeros((f_sz, f_sz)), sigma)
    #将坐标点坐标floor向下取整，计算出在矩阵中的位置，并限定在图像最大尺寸与【1，1】之间
        x = min(w, max(1, int(np.floor(point[0]))))
        y = min(h, max(1, int(np.floor(point[1]))))
    #超出范围的点舍弃
        if x > w or y > h:
            continue
    #根据窗口大小计算出左上角(x1,y1)和右下角坐标(x2,y2)
        x1 = x - int(f_sz/2)
        y1 = y - int(f_sz/2)
        x2 = x + int(f_sz/2)
        y2 = y + int(f_sz/2)
            
        dfx1 = 0
        dfy1 = 0
        dfx2 = 0
        dfy2 = 0
        change_H = False
    #判断高斯核尺寸是否超过图像边界如果超过则改变
        if x1 < 1:
            dfx1 = abs(x1) + 1
            x1 = 1
            change_H = True
        if y1 < 1:
            dfy1 = abs(y1) + 1
            y1 = 1
            change_H = True
        if x2 > w:
            dfx2 = x2 - w
            x2 = w
            change_H = True
        if y2 > h:
            dfy2 = y2 - h
            y2 = h
            change_H = True
    #计算裁剪后的区域在高斯滤波器核矩阵中的宽度和高度    
        x1h = 1 + dfx1
        y1h = 1 + dfy1
        x2h = f_sz - dfx2
        y2h = f_sz - dfy2
        
        if change_H:
            H = gaussian_filter(np.zeros((y2h - y1h + 1, x2h - x1h + 1)), sigma)
    #将高斯滤波器(H)加到矩阵 im_density 的相应位置上，以构建密度图
        im_density[y1-1:y2, x1-1:x2] += H
    
    return im_density

几何自适应核 python复现：

#几何自适应核
import numpy as np
from scipy.ndimage import gaussian_filter
import scipy
def compute_density_map(im, points):
    #根据图片大小生成全0矩阵
    h, w = im.shape[:2]
    im_density = np.zeros((h, w))
    
    #如果坐标点个数即人头数为1，则将该点对应的像素位置设置为最大值255，并返回
    if len(points) == 1:
        x1 = max(1, min(w, round(points[0, 0])))
        y1 = max(1, min(h, round(points[0, 1])))
        im_density[y1, x1] = 255
        return im_density
    
    pts = np.array(zip(np.nonzero(im)[1], np.nonzero(im)[0]))
    leafsize = 2048
    # build kdtree
    tree = scipy.spatial.KDTree(pts.copy(), leafsize=leafsize)
    # query kdtree
    distances, locations = tree.query(pts, k=4)

    #对每个标注点开始遍历
    #定义一个高斯窗口的尺寸(f_sz)和标准差(sigma)，并使用fspecial函数创建一个高斯滤波器(H)
    for point in points:
        f_sz = 15
    #kd数搜索出离该目标点最近的4个标注点距离，去除最近的，剩余3个距离相加取平均，再乘上文章中取的beta=0.3
        sigma = (distances[point][1]+distances[point][2]+distances[point][3])*0.3/3
    #生成高斯核
        H = gaussian_filter(np.zeros((f_sz, f_sz)), sigma)
    #将坐标点坐标floor向下取整，计算出在矩阵中的位置，并限定在图像最大尺寸与【1，1】之间
        x = min(w, max(1, int(np.floor(point[0]))))
        y = min(h, max(1, int(np.floor(point[1]))))
    #超出范围的点舍弃
        if x > w or y > h:
            continue
    #根据窗口大小计算出左上角(x1,y1)和右下角坐标(x2,y2)
        x1 = x - int(f_sz/2)
        y1 = y - int(f_sz/2)
        x2 = x + int(f_sz/2)
        y2 = y + int(f_sz/2)
            
        dfx1 = 0
        dfy1 = 0
        dfx2 = 0
        dfy2 = 0
        change_H = False
    #判断高斯核尺寸是否超过图像边界如果超过则改变
        if x1 < 1:
            dfx1 = abs(x1) + 1
            x1 = 1
            change_H = True
        if y1 < 1:
            dfy1 = abs(y1) + 1
            y1 = 1
            change_H = True
        if x2 > w:
            dfx2 = x2 - w
            x2 = w
            change_H = True
        if y2 > h:
            dfy2 = y2 - h
            y2 = h
            change_H = True
    #计算裁剪后的区域在高斯滤波器核矩阵中的宽度和高度    
        x1h = 1 + dfx1
        y1h = 1 + dfy1
        x2h = f_sz - dfx2
        y2h = f_sz - dfy2
        
        if change_H:
            H = gaussian_filter(np.zeros((y2h - y1h + 1, x2h - x1h + 1)), sigma)
    #将高斯滤波器(H)加到矩阵 im_density 的相应位置上，以构建密度图
        im_density[y1-1:y2, x1-1:x2] += H
    
    return im_density