【无标题】

实践五 图的遍历算法的应用——最小生成树的求解

• 实验目的：

本实验旨在通过实现Prim算法和Kruskal算法，探究图的遍历算法在求解最小生成树问题中的应用。通过实验，加深对最小生成树概念和算法原理的理解，并验证两种算法的正确性和效率。

• 实验内容：

图的遍历算法的应用，最小生成树的求解

三、实验结果

最小生成树是一种图论中常用的算法，用于在带权连通图中找到一棵权值和最小的生成树。常用的算法包括Prim算法和Kruskal算法。

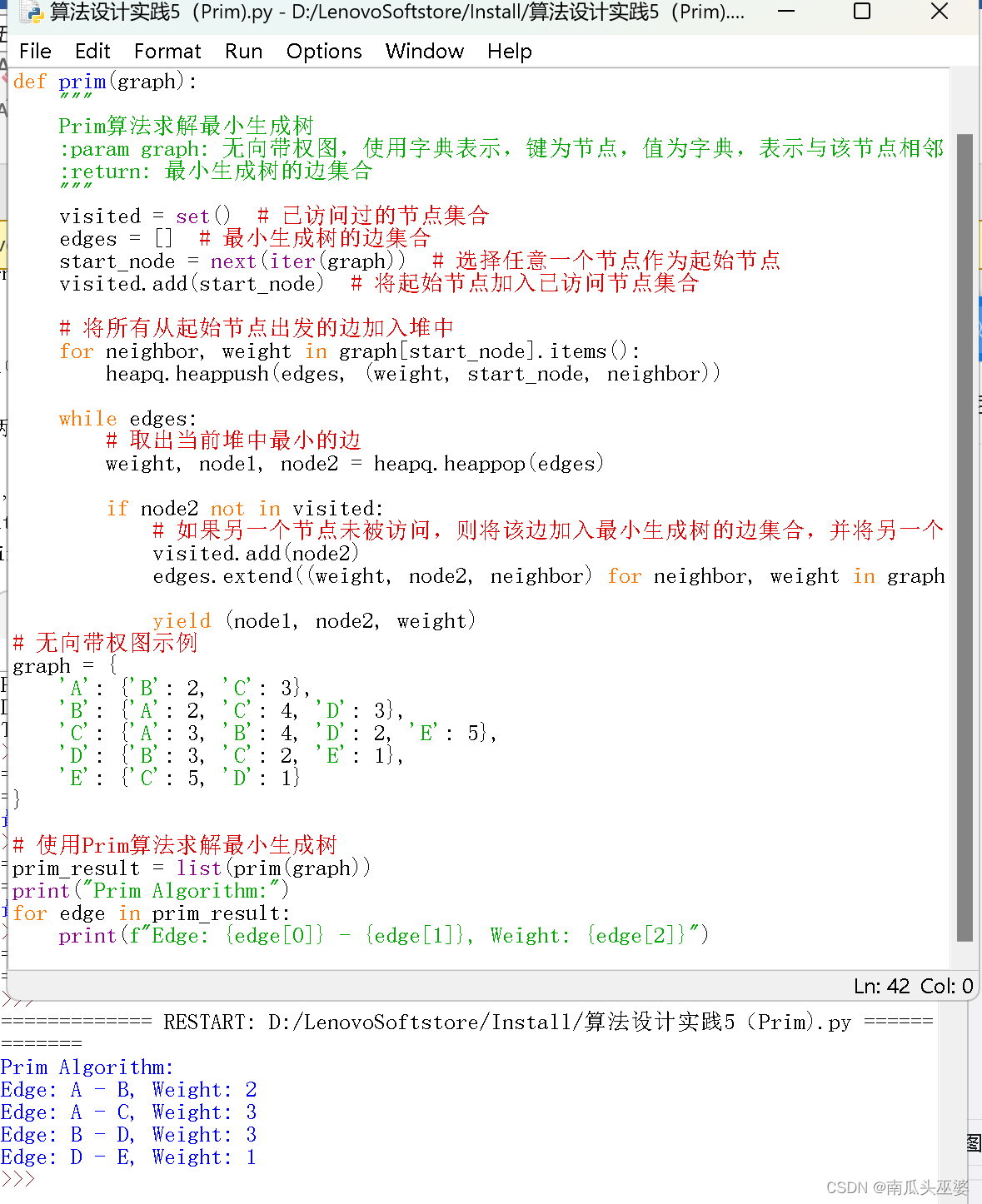
1．Prim算法的实现源程序:

Prim算法的实现源程序:
import heapq

def prim(graph):
    """
    Prim算法求解最小生成树
    :param graph: 无向带权图，使用字典表示，键为节点，值为字典，表示与该节点相邻的节点及边权重
    :return: 最小生成树的边集合
    """
    visited = set()  # 已访问过的节点集合
    edges = []  # 最小生成树的边集合
    start_node = next(iter(graph))  # 选择任意一个节点作为起始节点
    visited.add(start_node)  # 将起始节点加入已访问节点集合

    # 将所有从起始节点出发的边加入堆中
    for neighbor, weight in graph[start_node].items():
        heapq.heappush(edges, (weight, start_node, neighbor))

    while edges:
        # 取出当前堆中最小的边
        weight, node1, node2 = heapq.heappop(edges)

        if node2 not in visited:
            # 如果另一个节点未被访问，则将该边加入最小生成树的边集合，并将另一个节点加入已访问节点集合
            visited.add(node2)
            edges.extend((weight, node2, neighbor) for neighbor, weight in graph[node2].items() if neighbor not in visited)

            yield (node1, node2, weight)
# 无向带权图示例
graph = {
'A': {'B': 2, 'C': 3},
'B': {'A': 2, 'C': 4, 'D': 3},
'C': {'A': 3, 'B': 4, 'D': 2, 'E': 5},
'D': {'B': 3, 'C': 2, 'E': 1},
'E': {'C': 5, 'D': 1}
}

# 使用Prim算法求解最小生成树
prim_result = list(prim(graph))
print("Prim Algorithm:")
for edge in prim_result:
print(f"Edge: {edge[0]} - {edge[1]}, Weight: {edge[2]}")

测试结果：

2.Kruskal算法的实现源程序：

def kruskal(graph):

    """

    Kruskal算法求解最小生成树

    :param graph: 无向带权图，使用字典表示，键为节点，值为字典，表示与该节点相邻的节点及边权重

    :return: 最小生成树的边集合

    """

    edges = []  # 图中所有的边

    nodes = set()  # 图中所有的节点



    # 将图中所有的边加入堆中

    for node, neighbors in graph.items():

        for neighbor, weight in neighbors.items():

            edges.append((weight, node, neighbor))

        nodes.add(node)



    # 将所有边按照权重排序

    edges = sorted(edges)



    parents = {node: node for node in nodes}  # 记录每个节点的父节点

    tree_edges = []  # 最小生成树的边集合



    for weight, node1, node2 in edges:

        if find(parents, node1) != find(parents, node2):

            # 如果两个节点不在同一个连通分量中，则加入最小生成树的边集合

            union(parents, node1, node2)

            tree_edges.append((node1, node2, weight))



    return tree_edges





def find(parents, node):

    """

    查找节点的根节点

    """

    while node != parents[node]:

        node = parents[node]

    return node





def union(parents, node1, node2):

    """

    合并两个节点所在的连通分量

    """

    root1, root2 = find(parents, node1), find(parents, node2)

    parents[root1] = root2



# 无向带权图示例

graph = {

    'A': {'B': 2, 'C': 3},

    'B': {'A': 2, 'C': 4, 'D': 3},

    'C': {'A': 3, 'B': 4, 'D': 2, 'E': 5},

    'D': {'B': 3, 'C': 2, 'E': 1},

    'E': {'C': 5, 'D': 1}

}

# 使用Kruskal算法求解最小生成树

kruskal_result = kruskal(graph)

print("\nKruskal Algorithm:")

for edge in kruskal_result:

    print(f"Edge: {edge[0]} - {edge[1]}, Weight: {edge[2]}")

测试结果：

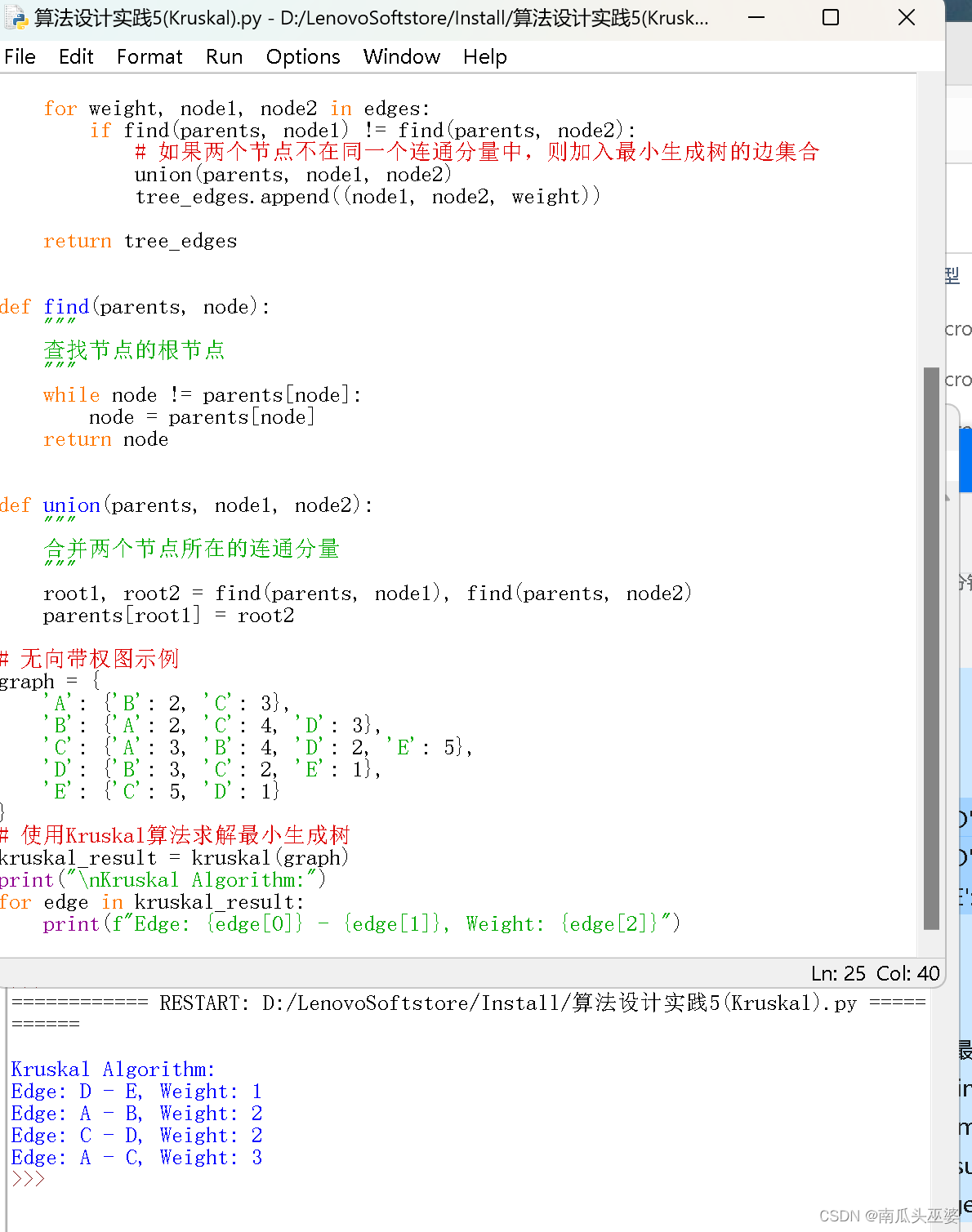
三、实验心得

通过本次实验，我对图的遍历算法在求解最小生成树问题中的应用有了更深入的理解。Prim算法和Kruskal算法是常用的最小生成树算法，它们分别从不同的角度解决了最小生成树的求解问题。

在实现过程中，我掌握了使用堆数据结构和并查集数据结构对边和连通分量进行管理的方法。通过验证算法的正确性，我确认了两种算法的准确性和可靠性，在分析算法效率的过程中，我发现Prim算法适用于稠密图，因为它以节点为中心，每次选择一个离已有最小生成树最近的节点；而Kruskal算法适用于稀疏图，因为它以边为中心，每次选择权值最小的边。因此，两种算法在不同规模图下的运行时间会有所差异。