背包问题（01，完全，多重，分组）

dp问题一般从两个方面考虑：1.状态表示 2.状态计算

1.01背包

有一个容量为v的背包，有n个物体，每个物体的体积是vi，价值是wi，在背包能装下的情况下找出最大能装多少价值的物品。（每件只有一个）

1.状态表示： f[i][j]这个形式表示的是从前i个物品里选，最大体积不超过j的方法的集合

这个数储存的是这个状态的某种属性：如最大价值，最小价值，在本题是最大价值

2.状态计算：最后求的状态应该是f[n][v]

f[i][j]可以划分为两个状态的集合：一种是不选i，一种是不选i

1.不选i的状态表示是f[i-1][j]（从前i-1个物品中选总体积不超过j的所有选择方法的集合的最大价值）

2.选i的状态表示是f[i-1][j-vi]+wi（前i-1个物品中选总体积不超过j-vi（给i留个体积确保他能装进去）的状态的最大价值最后再加上i的价值wi就说明最后的最大价值里一定选了i）。但是这个状态有一个条件，那就是j>=vi，意思是他要求最大不超过的体积一定要比i的体积大才能选i，不然就装不了i

我们要求最大值，这两个状态加起来就是总情况，且两个状态求的都是最大值，所以两个状态取max就是所求f[i][j]的值，即

f[i][j]=max (f[i-1][j] , f[i-1][j-vi]+ wi)

最朴素的二维代码是

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int n,m;
int v[1100],w[1100];
int f[1100][1110];
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		scanf("%d%d",&v[i],&w[i]);
	}
	for(int i=1;i<=n;i++){//因为i=0时表示的是从前0件物品中选，都是0所以从1开始
		for(int j=0;j<=m;j++){
			f[i][j]=f[i-1][j];//这个状态一定存在
			if(j>=v[i])f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);//**
		}
	}
	printf("%d",f[n][m]);
	return 0;
}

欧莫，我突然发现//**的地方max里的f[i][j]写成f[i-1][j]也可以，因为他们俩值一样。所以我记的话为了保持一致就全i-1好了

 这个是二维的，计算一般会超时，所以我们来把他进行一个优化，即删掉【i】这一维，当删掉i这一维时，变成了：

for(int i=1;i<=n;i++){
		for(int j=0;j<=m;j++){
			f[j]=f[j];//恒等式，可直接删除，但是删除之后的下面那个式子和原来表达的不一样
			if(j>=v[i])f[j]=max(f[j],f[j-v[i]]+w[i]);//这个式子中的j-v[i]恒小于j，所以在i-1层被算过了，我们要处理这种情况只用把j反转过来就好了，即：j=m,j>=v[i],j--
		}
	}

最终优化的版本是：

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int f[1100];
int v[1100],w[1100];
int main(){
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>v[i]>>w[i];
	}
	for(int i=1;i<=n;i++){
		for(int j=m;j>=v[i];j--){
			f[j]=max(f[j],f[j-v[i]]+w[i]);
		}
	}
	printf("%d",f[m]);
	return 0;
}

2.完全背包问题

题干同01背包，不同的是每件有无数个。

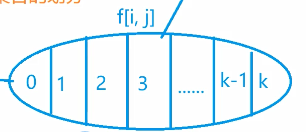
1.状态表示：因为每种有无数个物品，但是背包的能装的体积是有限的，所以他最多能装v/v[i]个i物品，，设他装k个i物品，那么不含i的状态表示就是f[i-1][j]，含k个i的状态表示是f[i-1][j-k*v[i]]+k*w[i],很容易发现当k=0时就是f[i-1][j],所以我们可以把他总结成通式：f[i-1][j-k*v[i]]+k*w[i],然后再枚举k从0到v/v[i]即可。

最朴素的代码（但是会t，只是用来理解）

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int n,m;
int v[1100],w[1100];
int f[1100][1110];
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		scanf("%d%d",&v[i],&w[i]);
	}
	for(int i=1;i<=n;i++){//因为i=0时表示的是从前0件物品中选，都是0所以从1开始
		for(int j=0;j<=m;j++){
			for(int k=0;k*v[i]<=j;k++){
				f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
			}
		}
	}
	printf("%d",f[n][m]);
	return 0;
}

 他t的原因是三层循环，所以我们优化的时候考虑删掉一层循环，考虑吧k的那层循环删掉。

我们先看一下f[i][j]包含的状态是什么：

f[i][j]=max(f[i-1][j], f[i-1][j-vi]+w, f[i-1][j-2*vi]+2*w....)

(不含物品i，含一个物品i，含两个物品i....这所有情况集合的最大值）

再看一下f[i][j-vi]包含的状态是什么：

f[i][j-v]=max(f[i-1][j-v] ,f[i-1][j-2*vi]+w ,f[i-1][j-3*vi]+2*w...)

(不含物品i，含一个物品i，含两个物品i....这所有情况集合的最大值）

对比这两个式子：

 可以总结出最后的式子与k无关：

f[i][j]=max(f[i-1][j],f[i][j-vi]+w)

但是f[i][j-vi]+w存在的情况是有条件的：j>=vi

所以完成了优化，代码是

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int n,m;
int v[1100],w[1100];
int f[1100][1110];
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++){
		scanf("%d%d",&v[i],&w[i]);
	}
	for(int i=1;i<=n;i++){//因为i=0时表示的是从前0件物品中选，都是0所以从1开始
		for(int j=0;j<=m;j++){
			f[i][j]=f[i-1][j];
			if(j>=v[i])f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
		}
	}
	printf("%d",f[n][m]);
	return 0;
}

 这里就要对01背包和完全背包来个对比了，两个代码唯一的区别就是01是从i-1层更新的，完全是从i层开始更新的。

我们要进行优化，把他优化成一维的话，因为都是第i层，所以直接把他i那一维删了就可以了。 

for(int i=1;i<=n;i++){
		for(int j=v[i];j<=m;j++){
			f[j]=max(f[j],f[j-v[i]]+w[i]);
		}
	}

多重背包问题：有n个物品，背包容量是m，第i个物品最多有si个，体积是vi，价值是wi，问背包最大价值能装多少。

思路和完全背包差不多，但是不同的是k的范围，完全背包是当k*v[i]<=m时循环，而这个给定了最大数量s[i]，所以条件变为k<=s[i]。

#include<iostream>
#include<algorithm>
using namespace std;
int f[105][105];
int s[105];
int v[105];
int w[105];
int n,m;
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>v[i]>>w[i]>>s[i];
	}
	for(int i=1;i<=n;i++){
		for(int j=0;j<=m;j++){
			for(int k=0;k<=s[i]&&k*v[i]<=j;k++){
				f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
			}
		}
	}
	printf("%d",f[n][m]);
	return 0;
}

 但是这样肯定会t，所以我们需要把他优化一下。

优化的方式就是二进制优化，一共有n个，我们可以把他分为1.2.4.8...2^k个一组，然后我们就可以用这么多组拼凑出来n，但是注意我们要保证1+2+4+...+2^k小于等于n，如果大于的话就超过了n，不符合要求，如果小于的话我们求出s=n-（1+2+4+...+2^k），然后就能拿1.2.4...2^k.s，这些数来凑n了，这样按二进制分组之后再做一遍01背包问题就能解决了。

#include<iostream>
#include<algorithm>
using namespace std;
const int N=25000;
int f[N];
int v[N];
int w[N];
int n,m;
int main(){
	cin>>n>>m;
	int cnt=0;
	for(int i=1;i<=n;i++){
		int v1,w1,s1;
		cin>>v1>>w1>>s1;
		int k=1;
		while(k<=s1){
			cnt++;
			v[cnt]=v1*k;
			w[cnt]=w1*k;
			s1-=k;
			k*=2;
		}
		if(s1>0){
			cnt++;
			v[cnt]=s1*v1;
			w[cnt]=s1*w1;
		}
	}
	for(int i=1;i<=cnt;i++){
		for(int j=m;j>=v[i];j--){
			f[j]=max(f[j],f[j-v[i]]+w[i]);
		}
	}
	printf("%d",f[m]);
	return 0;
}

分组背包问题：有n组物品，有一个最大体积为m的背包，每组有si种物品，每种物品的价值是w体积是w，且每组里只能挑一个物品，求最大价值。

将每组的物品当成01背包来做就好了。

.

#include<iostream>
#include<algorithm>
using namespace std;

int f[30000];
int s[105];
int v[105][105];
int w[105][105];
int main(){
	int n,m;
	cin >>n>>m;
	for(int i=1;i<=n;i++){
		cin>>s[i];//输入每组的个数
		for(int j=0;j<s[i];j++){//在各组的编号
			cin>>v[i][j]>>w[i][j];
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=m;j>=0;j--){//01背包模型，只能选一个
			for(int k=0;k<s[i];k++){//在每组的编号
				if(v[i][k]<=j){//当能装下才能更新
					f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);
				}
			}
		}
	}
	printf("%d",f[m]);
	return 0;
}

还有一些问题是问你装满背包的话最大价值是多少，如果不能装满输出no的那种，我们就把f全都赋值成负无穷。f[0]=0，然后剩下代码和上面一样，如果fm输出的是负无穷的话就表示不能把fn装满，直接输出no。