【Matlab入门】 第六章 统计基础及曲线拟合

引言

非常抱歉鸽了一段时间，2月23号换完内存后总怕我的鸡哥会自燃，所以前前后后倒腾了几天，现在换成了天选锐龙版，可以好好给各位码字了。
倘若你不是专业的统计人员也不要急着划走，因为本章涉及到的统计知识非常浅薄，谈不上专业。统计生成图表的方法可能会对你将来的工作汇报、数据处理有一定作用。并且加深对该软件的了解所以还在等待什么呢，进入本章的学习吧。
学习本章之前，请你务必掌握第一章内容，具体可以到我的matlab专栏查看(小声bb一句：关注点赞收藏更方便查找哦，老爷们赏光啦!)。

第四章 统计基础、曲线拟合和Matlab编程

本章将从统计图像和数据处理入手，再插入数据分析中最常用的曲线拟合，最后浅讲一下matlab编程，希望点进来的你可以认真查看，及时反馈。

一、统计基础

本部分只教你解决最基础的数据处理问题，导入数据已经在第一章介绍过，如果不了解请移步我的专栏。我们主要讲解统计图绘制、平均值和方差等的计算。

1.常见统计图的绘制

在excel已经成为大多数人技巧的当下，matlab的统计图显得那么匮乏、无力。但是作为统计不可缺少的一部分，我还是要介绍如何用该软件完成统计图绘制。并且在面对大规模数据时，这个软件比excel要厉害得多。
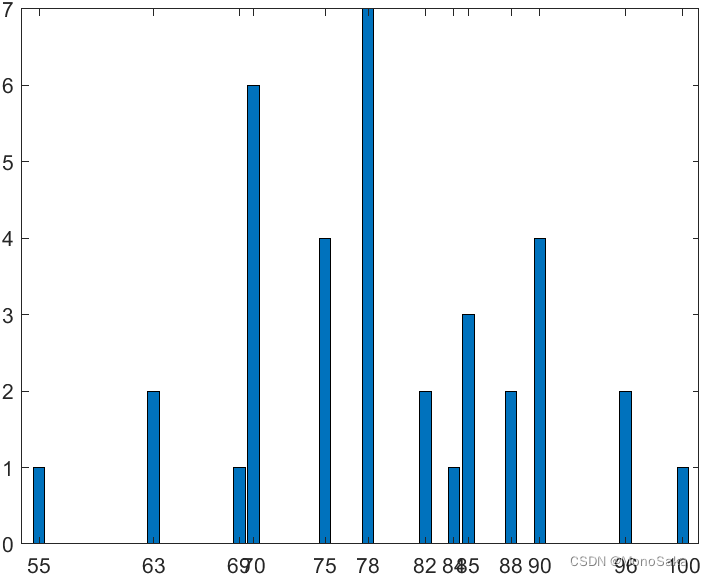
利用bar函数生成y关于x向量组的柱形图，第三章中已经介绍过该函数，为图像x轴和y轴建立标注和建立图注和图像标题的方法第三章也介绍过。以上办法建立的是竖状的条形图，为了减小各位的时间成本，我举一堆数据来生成一个条形图，例如
设想九年级的代数班有 36 位学生，学生在期中考中取得的分数及每个分数的学生是：
1 位学生得 100 分；2 位学生得 96 分；4 位学生得 90 分；2 位学生得 88 分；3 位学生得 85 分；1 位学生得 84 分；2 位学生得 82 分；7 位学生得 78 分；4 位学生得 75 分；6 位学生得 70 分；1 位学生得 69 分；2 位学生得 63 分；1 位学生得 55 分。现在我们要生成一个条形图，直接调用bar函数：

>> x = [55,63,69,70,75,78,82,84,85,88,90,96,100];
>> y = [1,2,1,6,4,7,2,1,3,2,4,2,1];
>> bar(x,y)

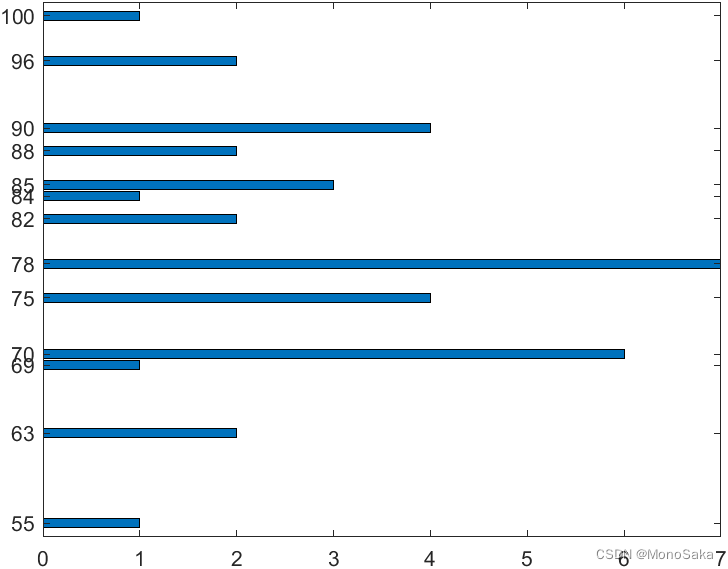
如何生成横条状的条形图呢，替换为barh函数即可：

>> x = [55,63,69,70,75,78,82,84,85,88,90,96,100];
>> y = [1,2,1,6,4,7,2,1,3,2,4,2,1];
>> barh(x,y)

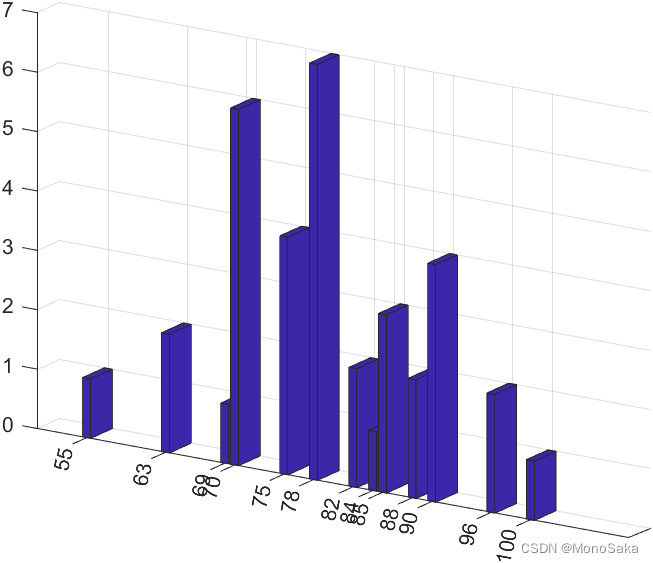
为了让图像更加直观，在专栏第三章介绍的bar3()函数可以上阵了：

>> x = [55,63,69,70,75,78,82,84,85,88,90,96,100];
>> y = [1,2,1,6,4,7,2,1,3,2,4,2,1];
>> bar3(x,y)

这是bar函数，你可否还记得我先前提到的stem函数？鄙人不才，对stem的了解还很肤浅，给大家推荐一篇文章：https://zhuanlan.zhihu.com/p/603526480#:~:text=stem3%28Z%29%20stem3%28X%2CY%2CZ%29%20stem3%28___%2C%22filled%22%29%20stem3%28___%2CLineSpec%29%20h,%3D%20stem3%28___%29%20%E7%94%A8%E6%B3%95%E5%92%8C%E5%90%AB%E4%B9%89%E5%90%8C%20stem%20%E4%B8%80%E6%A0%B7%EF%BC%8C%E5%8F%AA%E4%B8%8D%E8%BF%87%E5%A2%9E%E5%8A%A0%E4%BA%86%E7%AC%AC%E4%B8%89%E7%BB%B4%E7%9A%84%E5%9D%90%E6%A0%87%E3%80%82
点开链接即可看到详解

2.数据处理基本方法

Ⅰ求和

关于求和函数sum的用法在下方平均数部分详细介绍。

Ⅱ 平均数(具体有两种计算方法)

主要讨论算数平均数。

(1)算数平均数
①采用mean函数，主要用于对已知数组或矩阵元素平均值的计算，对前者计算直接得出所有元素平均值，对后者计算会算出每一列的平均值：

>> x = [1,3,5,7,9,11];
>> y = mean(x) %对x数组进行平均值计算

y =

     6

>> x = [1,2,3;4,5,6;7,8,9]; %对矩阵进行平均值的计算，可以看到结果是对每一列分别求平均值
>> y = mean(x)

y =

     4     5     6

>> x

x =

     1     2     3
     4     5     6
     7     8     9

②sum函数暴力计算
这个理解也很简单，利用sum函数对样本数据做求和，再直接除以样本量，这种办法需要利用到对数组或矩阵中元素的调用，还是以上述两个式子为例，采用sum直接计算：

>> x = [1,3,5,7,9,11]; %直接对数组内元素求和，不需要采用子元素提取语句
>> y = sum(x)

y =

    36

>> ave = y/6

ave =

     6

>> x = [1,2,3;4,5,6;7,8,9];
>> y = sum(x)

y =

    12    15    18

>> ave = y/3

ave =

     4     5     6
%注意，这里系统仍然对每一列进行了求和，这里要除的数字是3，不是9，否则无法得出准确结果

Ⅲ 计算标准偏差和中位数

前者使用的函数为std(a),后者函数为median(a)，a处为数组。

>> x = [1,3,5,7,9,11];
>> y = std(x)

y =

    3.7417

>> z = median(x)

z =

     6

对于打乱的数组，median函数依然适用：

>> x = [11,7,3,1,5,9];
>> y = median(x)

y =

     6

矩阵与上方的表现基本相同，还是输出每一列的中位数：

>> x

x =

     1     2     3
     4     5     6
     7     8     9

>> y = median(x)

y =

     4     5     6

二、曲线拟合(线性函数拟合和指数拟合)

1.线性函数拟合

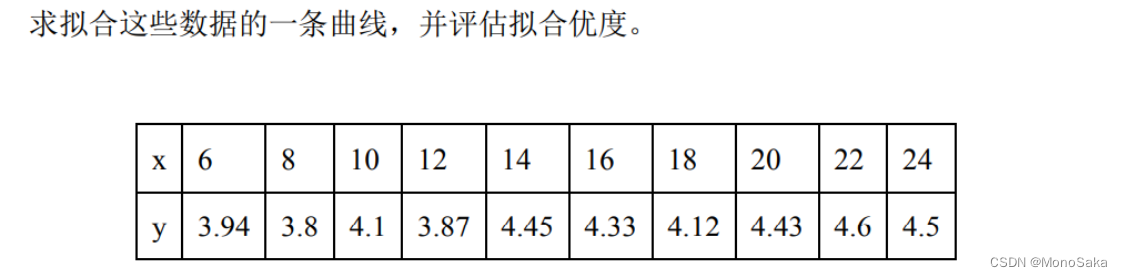
我们从一个例子入手：

Ⅰ 拟合曲线

①首先，绘制样本数据的散点图，初步判定拟合曲线的形状，强烈建议plot函数的option选项包含’o’或者’.'，保证画出的图为散点图而不是折线图(因为要拟合而不是绘制变化图线)。再按下hold on，保持这个散点图。

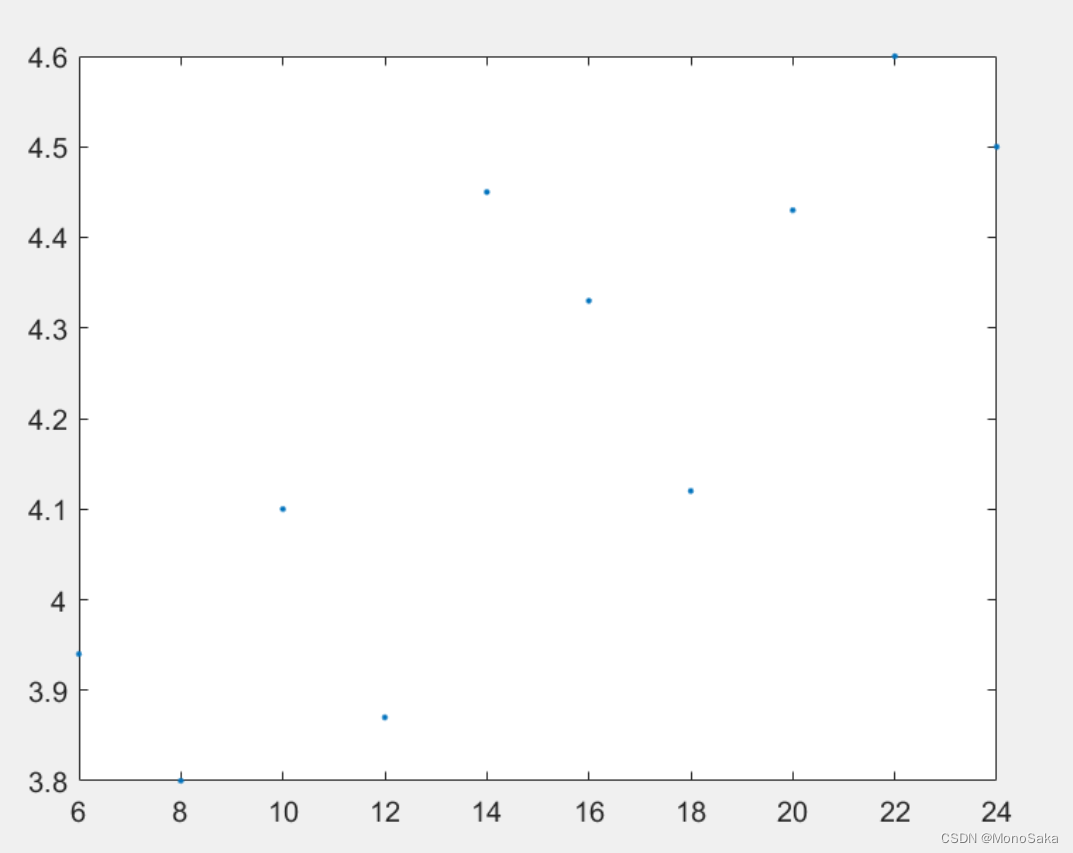
②调用polyfit函数(用于多项式曲线拟合)拟合样本数据，提取样本系数，调用格式为p = polyfit(x,y,n)，其中x和y表示需要拟合的坐标点，x和y在第一步中已经体现为数组，大小需要一样；n表示多项式拟合的次数，可以以泰勒展开式来类比，次数越高精度越高。用p来接收多项式拟合的项数，系数从高到低排列。

③使用接受到的p1和p2来计算拟合曲线：y=p1* x1+p2(本部分是线性拟合，所以采用了这样的模型)，再放到同一张图上。(由于拟合曲线需要平滑，这里并不采用题目中离散的x作为自变量，而是自定义了x1区间)

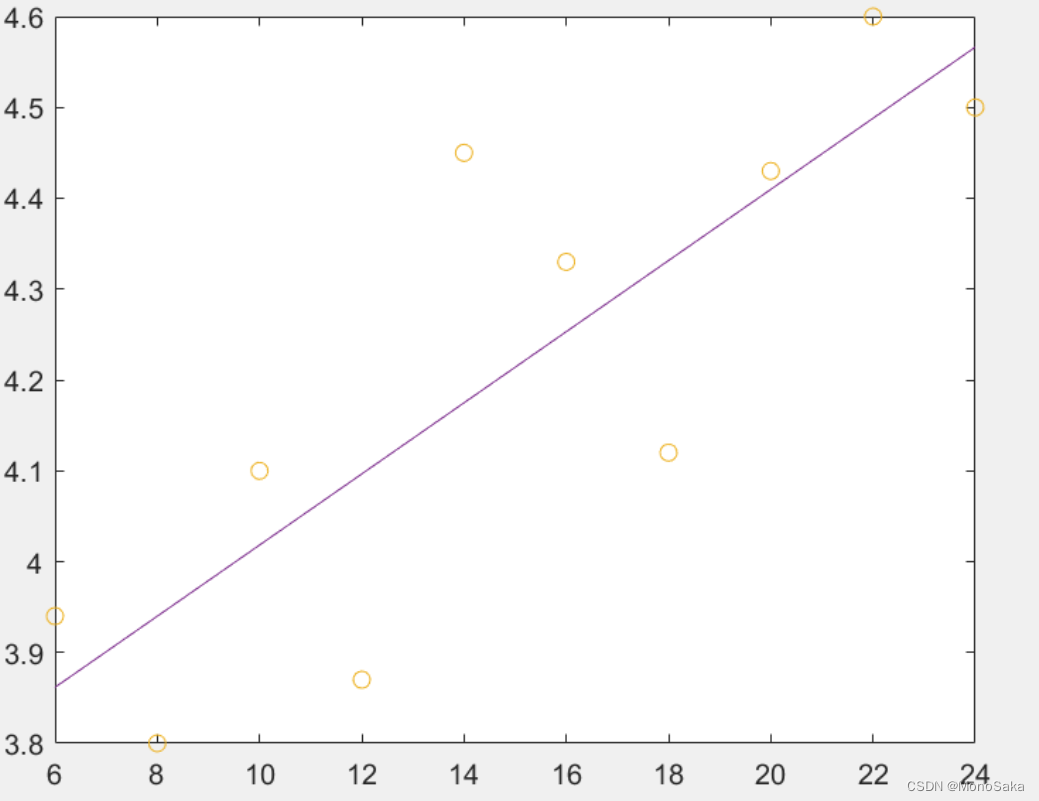
Ⅱ 计算拟合优度

拟合优度（Goodness of Fit）是指回归直线对观测值的拟合程度。拟合优度越接近1，代表拟合效果越好，越小拟合效果越差。
其计算方法如下：

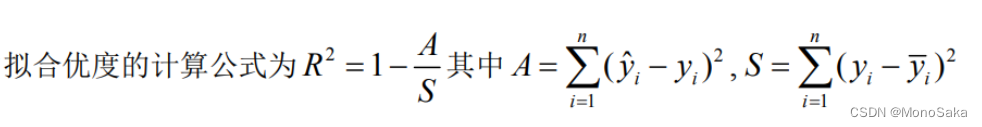
①A的计算：通过yn=p1* x+p2计算出每个拟合值，调用sum函数即可求出A
②S的计算：直接调用mean函数求得y这一数组的平均值，再通过sum函数算出S
③求出拟合优度，如代码块所示：

>> x = [6:2:24];
>> y = [3.94,3.8,4.1,3.87,4.45,4.33,4.12,4.43,4.6,4.5];
>> p = polyfit(x,y,1);
>> a = p(1);b = p(2);
>> yn = a*x + b;
>> A = sum((yn-y).^2)

A =

    0.2274

>> S = sum((y - mean(y)).^2)

S =

    0.7332

>> R2 = 1 - A / S

R2 =

    0.6899

Ⅲ 计算RMSE误差(均方根误差)

均方根误差是预测值与真实值偏差的平方与样本个数n比值的平方根，在实际测量中，n总是有限，真值只能用最佳值来代替。标准误差对一组测量中的特大或特小误差反映非常敏感，所以，标准误差能够很好地反映出测量的精密度。标准差是用来衡量一组数自身的离散程度，而均方根误差是用来衡量观测值同真值之间的偏差，它们的研究对象和研究目的不同，但是计算过程类似。在这里放出RMSE的计算方法：

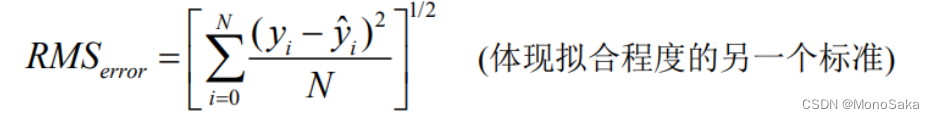
即输入RMS=sqrt((sum((y-yn).^2))/N)，其中N为样本数量。RMS越小，拟合效果越好。
还是以上述例子作为演示，代码如下方所示：

>> x = [6:2:24];
>> y = [3.94,3.8,4.1,3.87,4.45,4.33,4.12,4.43,4.6,4.5];
>> p = polyfit(x,y,1);
>> a = p(1);b = p(2);
>> yn = a*x + b;
>>> RMS = sqrt(sum((yn-y).^2)/10)

RMS =

    0.1508

Ⅳ 二次多项式拟合

这里还是借用泰勒展开的模型类比，不妨回忆一下e^x的展开式，当保留的次数越高，展开的结果也就越接近真值，以此类推，采用一次线性的方式拟合效果不够好的时候，我们可以使用二次多项式来拟合，这个次数并不限制，但是可以预见的，对于同一部分数据，次数越大假设为n，和n-1次数的拟合效果差别极其微小，所以再高次也并没有多大意义。还是以上方例子作为演示，对polyfit函数做一些小改动即可。

>> x = [6:2:24];
>> y = [3.94,3.8,4.1,3.87,4.45,4.33,4.12,4.43,4.6,4.5];
>> p = polyfit(x,y,2);
>> a = p(1);b = p(2);c = p(3); 
>> yn = a*x.^2 + b*x + c;
>> N = 10;RMS = sqrt(sum((yn-y).^2)/N)

RMS =

    0.1507

>> A = sum((yn-y).^2)
>> S = sum((y - mean(y)).^2)
>> R2 = 1 - A / S

R2 =

    0.6902

和上方线性拟合的结果做对比，我们可以看到拟合效果变好了，可能在大规模数据下RMS的波动幅度更加大，二次拟合效果会更加显著，各位自行尝试。
其次，可以看到我们仅仅改动了polyfit函数中的数字和次数，对于多项同理，用几项拟合，就改动为对应数字。但是注意要用对应个数的变量来接收polyfit函数的输出结果，并且修改yn的计算方式，否则容易产生牛头不对马嘴的情况，使得计算结果错误。

2.指数拟合

Ⅰ 指数拟合演示

polyfit函数不仅可以拟合多项式，还可以拟合指数形式的数据。指数拟合是利用指数函数y=exp(ax+b)对观测数据进行拟合，使误差平方和最小。Matlab对指数拟合没有提供专门的函数支持，通常利用一阶多项式拟合来解决指数函数拟合问题。对上式两边取对数，得到lny=ax+b，因此指数函数拟合转化为以 x和ln y为变量的一阶多项式拟合问题。
现在对y = 1-x^(1/2)在[0,0.99]的采样数据作指数函数拟合，求出指数函数的具体形式、在同一个坐标系下绘制指数拟合曲线及采样数据图，并绘图观察指数函数的拟合误差(拟合值和真值的差值)。
在这里我们调用polyval函数来计算拟合函数polyfit在x的值，方便放入exp函数从而转变为原函数，详情见代码注释。

>> x = 0:0.01:0.99;
>> y = 1 - sqrt(x); 
>> p = polyfit(x,log(y),1);
>> a = p(1);b = p(2);
>> yn = exp(polyval(p,x));%调用polyval以简便计算拟合值并转换
>> plot(x,y,'k',x,yn,'r')
>> xlabel('x'),ylabel('y');legend('采样数据','拟合曲线');title('指数拟合曲线');

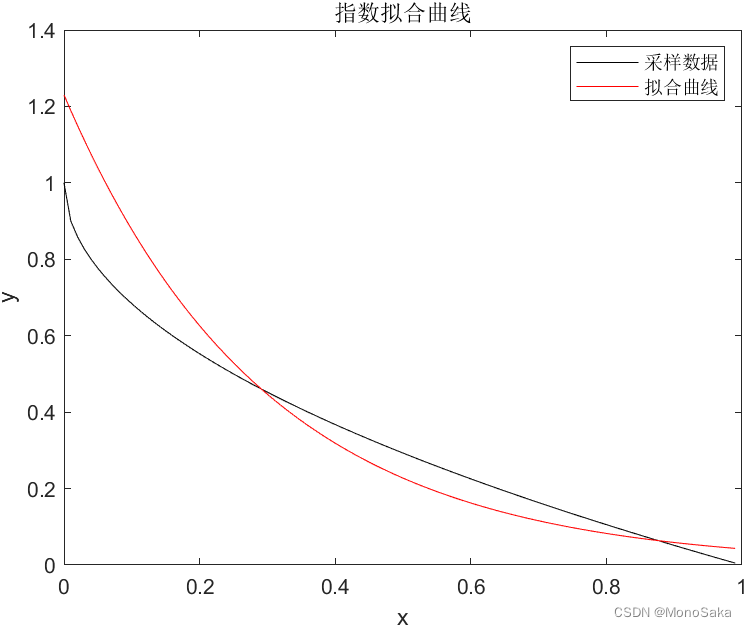
Ⅱ 多想一步：二次指数拟合是否精度更高？

我们可以预想到，如果增高次数，可能还会提高精度，先计算出本例一次拟合的拟合优度和RMS误差(取20个精度的x，即均匀取20个样本数据)。由于对数拟合次数提高的结果非常接近，我们还是让结果以高精度long形式显示而不是short(改变小数显示方式的办法在我的前几章中，请查阅)：

>> x = 0:0.01:0.99;y = 1 - sqrt(x);p = polyfit(x,log(y),1);
>> a = p(1);b = p(2);y1 = exp(polyval(p,x));
>> A = sum((y1-y).^2);S = sum((y - mean(y)).^2);R2 = 1 - A / S

R2 =

   0.823525152562285
   
>> N = 20;RMS = sqrt(sum((y1-y).^2)/N)

RMS =

   0.225182585911919

再提高次数，看是否会让精度提高，：

>> x = 0:0.01:0.99;y = 1 - sqrt(x);p = polyfit(x,log(y),2);
>> a = p(1);b = p(2);c = p(3);y1 = exp(polyval(p,x));
>> A = sum((y2-y).^2);S = sum((y - mean(y)).^2);R2 = 1 - A / S

R2 =

   0.918607698296766

>> N = 20;RMS = sqrt(sum((y2-y).^2)/N)

RMS =

   0.152927313616245

肉眼可见地提高了，可见对于线性拟合适用的规律对于对数也同样适用。(我第一次试验结果居然是精度降低，困扰了好多天)