【算法】力扣- 背包问题

关于背包问题,推荐卡哥的视频,结合代码随想录食用,效果绝佳!!!

传送门:

带你学透0-1背包问题！| 关于背包问题，你不清楚的地方，这里都讲了！| 动态规划经典问题 | 数据结构与算法_哔哩哔哩_bilibili

带你学透01背包问题（滚动数组篇） | 从此对背包问题不再迷茫！_哔哩哔哩_bilibili

带你学透完全背包问题！ 和 01背包有什么差别？遍历顺序上有什么讲究？_哔哩哔哩_bilibili

好了,开始今天正文:  

这是一篇纯分享总结内容的文章,想get背包问题的⬆  强推卡哥的讲解视频

什么是背包问题?

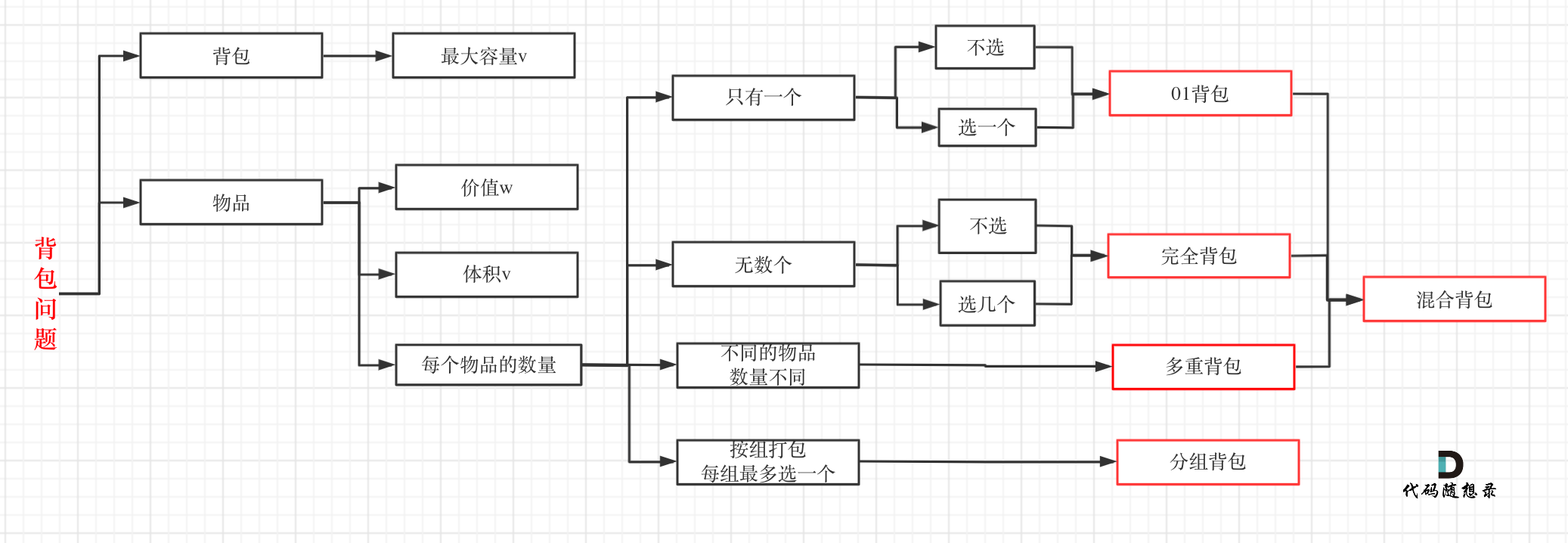
我们一般使用weights[],values[]数组来存贮每个物品的重量和价值

01 背包

有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

对于01 背包问题

二维dp

dp数组的含义:

dp[i][j] 表示0 - i物品任取放入背包容量为j的背包中的最大价值

递推公式:

dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - W[j] + V[i])

dp[i-1][j-w[i]]表示选了当前第i个物品后只能从前i-1个物品中进行选择，并且扣除了当前第i个物品的weight；

而dp[i][j]的推导由取i 和 不取i物品获得的最大价值 取较大值进行推导的

初始化:

for(int j = 1; j <= n; j++) {            
    if(j >= weights[0]) {                
        dp[0][j] = values[0];            
    }        
}

二维dp代码:

import java.util.*;
 
public class Main {
    public static void main (String[] args) {
        Scanner sc = new Scanner(System.in);
        int m = sc.nextInt();
        int n = sc.nextInt();
         
        int[] values = new int[m];
        int[] weights = new int[m];
        for(int i = 0; i < m; i++) {
            weights[i] = sc.nextInt();
        }
        for(int i = 0; i < m; i++) {
            values[i] = sc.nextInt();
        }
         
        // dp[i][j] 表示0-i物品任取放入容量为j的背包中产生的最大价值
        int[][] dp = new int[m][n + 1];
        // 初始化
        for(int j = 1; j <= n; j++) {
            if(j >= weights[0]) {
                dp[0][j] = values[0];
            }
        }
         
        for(int i = 1; i < m; i++) {    // 先物品
            for(int j = 0; j <= n; j++) {   // 后背包容量
                if (j < weights[i]) {
                    dp[i][j] = dp[i - 1][j];
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weights[i]] + values[i]);
                }
            }
        }
        System.out.println(dp[m - 1][n]);
    }
}

一维dp(滚动数组)

对于背包问题其实状态都是可以压缩的。

在使用二维数组的时候，递推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上，表达式完全可以是：dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);

与其把dp[i - 1]这一层拷贝到dp[i]上，不如只用一个一维数组了，只用dp[j]（一维数组，也可以理解是一个滚动数组）。

这就是滚动数组的由来，需要满足的条件是上一层可以重复利用，直接拷贝到当前层。

dp数组的含义:

dp[i][j] 表示背包容量为j的背包中的最大价值

递推公式:

dp[j] = max(dp[j],dp[j - W[i]] + V[i]);

这里因为是滚动数组,每次都是滚动升级,需要依靠前面的状态

需要注意的是,在遍历背包的时候需要倒序遍历确保所有物品最多只取一次

一维dp代码:

import java.util.*;
 
public class Main {
    public static void main (String[] args) {
        // 滚动数组
        Scanner sc = new Scanner(System.in);
        int m = sc.nextInt();
        int n = sc.nextInt();
         
        int[] values = new int[m];
        int[] weights = new int[m];
        for(int i = 0; i < m; i++) {
            weights[i] = sc.nextInt();
        }
        for(int i = 0; i < m; i++) {
            values[i] = sc.nextInt();
        }
         
        // dp[j] 表示放入容量为j的背包中产生的最大价值
        int[] dp = new int[n + 1];
        // 初始化
        dp[0] = 0;
         
        for(int i = 0; i < m; i++) {    // 先物品
            for(int j = n; j >= 0; j--) {   // 后背包容量
                if(j >= weights[i]) {
                    dp[j] = Math.max(dp[j],dp[j - weights[i]] + values[i]);
                }
            }
        }
        System.out.println(dp[n]);
    }
}

完全背包

有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。

完全背包和01背包问题唯一不同的地方就是，每种物品有无限件。

二维dp

dp数组的含义:

dp[i][j] 表示0 - i物品任取放入背包容量为j的背包中的最大价值

递推公式:

dp[i][j] = max(dp[i - 1][j], dp[i][j - W[j] + V[i])

dp[i][j-w[i]]表示尽管我选了当前物品，也把当前物品的weight从背包容量中扣除了，但是我仍然可以在这i个物品中继续选择。

与01背包问题其区别在于每个物品是否可重复选。

二维dp代码:

import java.util.*;
 
public class Main {
    public static void main (String[] args) {
        Scanner sc = new Scanner(System.in);
         
        int n = sc.nextInt();
        int v = sc.nextInt();
         
        int[] weights = new int[n];
        int[] values = new int[n];
        for(int i = 0; i < n; i++) {
            weights[i] = sc.nextInt();
            values[i] = sc.nextInt();
        }
         
        int[][] dp = new int[n][v + 1];
        for(int j = 0; j <= v; j++) {
            if(j == 0) {
                dp[0][j] = 0;
            } else {
                int k = j / weights[0];
                dp[0][j] = k * values[0];
            }
        }
         
        for(int i = 1; i < n; i++) {
            for(int j = 0; j <= v; j++) {
                if(j < weights[i]) {
                    dp[i][j] = dp[i - 1][j];
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j],dp[i][j - weights[i]] + values[i]);
                }
            }
        }
         
        System.out.println(dp[n - 1][v]);
    }
}

一维dp

与01背包问题代码区别就是在遍历背包数量的时候使用正序遍历

其中原由: 代码随想录 (programmercarl.com)

一维dp代码:

import java.util.*;
 
public class Main {
    public static void main (String[] args) {
        Scanner sc = new Scanner(System.in);
         
        int n = sc.nextInt();
        int v = sc.nextInt();
         
        int[] weights = new int[n];
        int[] values = new int[n];
        for(int i = 0; i < n; i++) {
            weights[i] = sc.nextInt();
            values[i] = sc.nextInt();
        }
         
        int[] dp = new int[v + 1];
         
        for(int i = 0; i < n; i++) {
            for(int j = weights[i]; j <= v; j++) {
                dp[j] = Math.max(dp[j],dp[j - weights[i]] + values[i]);
            }
        }
        System.out.println(dp[v]);
    }
}