考研计组第二章定点数的加减运算以及溢出判断

目录

一.原码加减法的逻辑

1.1 原码的加法运算逻辑

1.2 原码的减法逻辑

减法转变为加法 

二. 补码的加减法逻辑 

2.1 补码的加法原理

例题一 

2.2 补码的减法运算原理

例题二： 

三. 用计算机实现溢出判断 

3.1 溢出原理

3.2 溢出判断 

方法一： （单符号位补码模2补码）

方法二： 

溢出表达式为：

方法三： 双符号位判断溢出（双符号位补码模4补码）

 溢出表达式为：

---

回顾一下😋

在之前学习当中我们知道了讨论加减运算一般不讨论反码，只所以这篇讨论原码补码😘

一.原码加减法的逻辑

1.1 原码的加法运算逻辑

1. 正+正 = 绝对值相加，结果为正
2. 负+负 = 绝对值相加，结果为负
3. 正+负 = 绝对值大的 - 绝对值小的，最后的结果的正负与绝对值大的相同
4. 负+正 = 绝对值大的 - 绝对值小的，最后的结果的正负与绝对值大的相同

1.2 原码的减法逻辑

由于原码的减法实现起来不是很方便，所以我们需要 转变思路，将其转变成，方便的加法操作

减法转变为加法 

将“减数”的符号位取反，转变为加法

正 - 负 = 正 + 正

正 - 正 = 正 + 负

负 - 负 = 负 + 正

负 - 正 = 负 + 正

从上面大家可以看出来，这个逻辑用电路实现起来太难了 😫😫😫😫😫，所以我们一般使用不补码来进行加减。

二. 补码的加减法逻辑 

在前面的文章我们提到过，补码的加减不需要考虑符号位，因为符号位也同样参与运算

 如题：设机器字长为8位（含一位符号位），A = 15，B=-24，求【A+B】补和【A-B】补

2.1 补码的加法原理

例题一 

直接相加，符号位也相加，逢二进一

原码->补码：正数补码一样；负数先将原码转变成反码，在把反码末尾加1 ，具体的操作可以参考

我之前的一篇文章，原反补码计算https://mp.csdn.net/mp_blog/creation/editor/133816890

2.2 补码的减法运算原理

将 -【B】补 转换成 +【-B】补

求【-B】补可以先求B的原码，具体步骤可看计组考研第二章 定点数的移位计算-CSDN博客

• 负数补转原码的步骤：补码->原码：将符号位位保持不变，然后将其他位按位取反+1 
• 找到右边第一个1和之后的数与原码一样，1左边的数与反码一样，将1左边的全部取反可以得原码
• 【-B】补= 【B】补全部位包括符号位全部取反

（1） 

例题二： 

 

 由这题可以看出两个正数相加却等于负数，两个负数相加却等于正数，说明补码相加会存在溢出的情况

三. 用计算机实现溢出判断 

3.1 溢出原理

 会出现上溢和下溢的情况

• 正数 + 正数 会发生上溢
• 负数 + 负数 会发生下溢
• 正数+负数不会发生溢出 

3.2 溢出判断 

方法一： （单符号位补码模2补码）

采用一位符号位设A的符号位为。B的符号位为,运算结果的符号位为,则溢出表达式为

注意 🐾这里的+号表示的是或运算即全0为假，一真即真。三个值是且运算

如 上题【A+C】补的溢出表达式为 V = 000+111 = 1表示这里存在溢出 

【B-C】 V = 111+000 = 1 表示溢出

方法二： 

采用一位符号位，根据数据位进位情况判断溢出符号位的进位, 最高数值位的进位

根据数值位进位判断溢出

	符号位的进位	最高数值位的进位
上溢	0	1
下溢	1	0

与 不会同时有溢出

溢出表达式为：

V =    

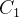
当 V = 0时表示没有溢出

当V = 1时表示有溢出

方法三： 双符号位判断溢出（双符号位补码模4补码）

用两个符号位，多出来的一个符号位并不占用存储空间只是运算时复制了一个，符号位也都参与运算，正为00，负为11。如果运算结果：

运算结果为01则是上溢

运算结果为10则是下溢

如【A+C】补 = 00，0001111 + 00，1111100 = 01，0001011 上溢

    【B-C】补 = 11，1101000 + 11，0000100 = 10，1101100 下溢 

 溢出表达式为：

两个符号位异或，V = 0 表示没有溢出，V = 1 表示有溢出