一、 神经网络的概念及其结构
深度学习通常指通过训练多层网络结构对未知数据进行分类或回归。深度神经网络的基本思想是构建多层网络,以期通过多层的高层次特征来表示数据的抽象语义信息,获得更好的特征鲁棒性。
人工神经网络(ANNs)是一种模仿动物神经网络行为特征、进行分布式并行信息处理的算法数学模型。这种网络通过内部大量节点之间的相互连接关系调整来达到处理信息和自学习、自适应的目的。神经网络类型繁多,其中最重要的是多层感知机(MLP)。为了详细介绍神经网络,我们先从最简单的神经网络开始说起。
感知机于1957年由 Rosenblatt 提出,是基于支持向量机的一种神经网络。受生物学启发而设计,类似于人类的神经系统,由许多神经元构成。神经元通过树突接收输入信号,形成微弱的生物电刺激,在细胞核内进行综合处理。当信号达到一定的阈值时,神经元被激活并输出信号,形成信号传递。神经元进行感知的工作原理如此。
下面是简单的感知机模型:
 图3.1 感知机结构
图3.1 感知机结构
多层感知机由感知机推广而来,最主要的特点是有多个神经元层,因此也叫深度神经网络,多层感知机的第i层的每个神经元和第i-1层的每个神经元都有连接。
 二、损失函数与得分函数
二、损失函数与得分函数
得分函数是用来评估模型输出的结果的质量的函数,通常是一个数值,在分类任务中,得分函数可以是softmax函数,将模型输出的概率转化为类别得分;在SR技术(一种图像增强技术,通过数据集让机器学习低清图像和高清图像的差距,最后将学习到的成果进行应用)中,得分函数可以是PSNR(峰值信噪比)、SSIM(结构相似性指标)等,用于衡量图像质量。
损失函数是用来衡量模型预测值与真实值之间的差异的函数,通常是一个数值。在分类任务中,常用的损失函数有交叉熵损失函数、对数损失函数等;在SR技术中,常用的损失函数有均方误差(MSE)和绝对误差(MAE)等,用于衡量重建图像与原始图像之间的差异。
损失函数就是用来评估目标与实际的差距,再通过得分函数转换为实际分数
我们想要知道我们训练得到的感知机好不好,我们就要通过的得分函数去判断。举个例子,低分辨率图像x通过一个复杂的感知机得到一个高分辨率图像y,最后我们通过y,z作为参数得到损失函数MSE或者MAE,再通过损失函数得到的损失值计算PSNR。
下面是基于深度学习SR技术计算得分函数和损失函数图示:

三、 正向传播与反向传播
在神经网络中我们通过输入层得到的参数,放入神经网络模型计算,从前往后得到最终值的过程,我们称之为正向传播。
反向传播是一个训练人工神经网络的一种方法。与正向传播相反,其在神经模型中的计算,是一个从前往后的过程,在模型进行学习的过程中,我们希望找到损失函数中的最小值,使模型达到更优。反向传播计算的过程就是建立在梯度下降法的基础上,因为在一般的神经网络中,一层的网络输入就是上一层网络的输出,网络层的逐层叠加的过程,我们可以将其看作函数复合的过程,基于这个原理,我们可以将损失函数向前展开,通过微分操作和链式法则,从神经网络的末尾开始,调节各层神经网络的权重,以找到损失函数的最小值。
梯度下降法是反向传播的重要基础。在多变量函数中,梯度是一个向量,向量有方向,梯度的方向就指出了函数在给定点的上升最快的方向,那么梯度的反方向就是在给定点下降最快的方向,这个方向正是我们反向传播过程中所需要的。我们要找到函数的最小值,就是通过微分找到梯度的方向一点一点使函数值下降,找到函数的最小值。
下面是个简单的例子:
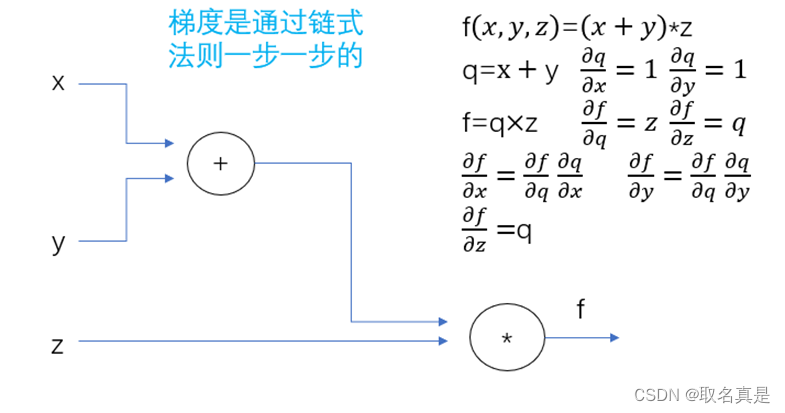
我们先通过输入的参数与当前每层网络结构的权重进行计算,得到最终结果,通过得到的结果与理想的结果进行对比通过损失函数和得分函数得到损失值和指标,然后通过链式法则把误差展开至隐藏层,再展开至输出层,在更新权重,通过新的权重我们又通过正向传播得到新的损失值和指标,在进行反向传播。如此反复,这便是机器学习的过程。
四、激活函数
在此前我们提出的网络模型中,里面包含的计算都是线性的,只有线性变换的模型表达能力是不够的,在这里我们引入的激活函数。
激活函数的作用是为神经网络引入非线性因素,使其能够更好地拟合复杂的非线性模式。在神经网络中,每个神经元都需要一个激活函数来决定它的输出值。激活函数通过对输入值进行非线性变换,将其映射到一个新的输出值范围内,通常是[0,1]或[-1,1]。这样可以使神经网络能够更好地处理复杂的输入数据。
下图是加入激活函数的感知机:
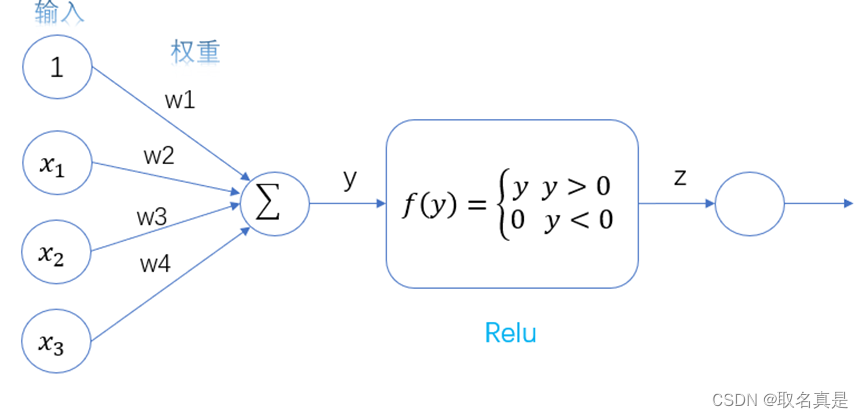 下面我们来介绍一下常用的激活函数:
下面我们来介绍一下常用的激活函数:
1、sigmoid激活函数
公式:
图像: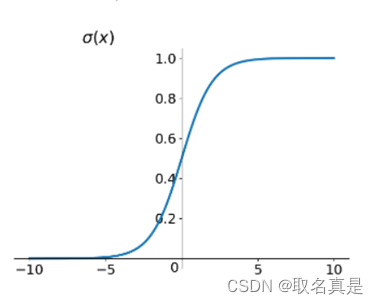
当运算结果得到的值很小的时候,由于该函数的导数很小,若一个网络中使用了多个该激活函数,根据链式法则,反向传播时,很容易发生梯度消失现象。
2、relu激活函数
公式: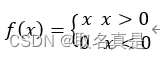
图像:
relu激活函数的优势在于是它在计算上比其他激活函数更加简单,并且在处理大型数据集时具有更好的收敛性能。另外,relu激活函数还能够有效地缓解梯度消失问题,使得神经网络能够更好地训练。因此,在实际应用中,relu激活函数是最常用的激活函数。
其他相关文章:

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










