数值积分的基本原理和方法（复合梯形、复合Simpson、龙贝格）

目录

一、实验目的

二、实验题目及要求

三、实验环境

四、实验内容

问题的求解算法及数据结构（要求画流程图）

源程序清单

程序运行结果及分析

实验总结

---

一、实验目的

1、了解数值积分的基本原理和方法；

2、熟练掌握复化梯形公式、复化 Simpson 公式及其截断误差的分析；

二、实验题目及要求

实验题目

实验要求

1、认真分析题目的条件和要求，复习相关理论知识，选择适当的解决方案和算法；

2、编写上机实验程序，作好上机前的准备工作；

3、上机调试程序，并试算各种方案，记录计算的结果（包括必要的中间结果）；

4、对实验结果进行分析、归纳、总结。

三、实验环境

1. 硬件环境：计算机

2. 软件环境：win10下的Devc++

四、实验内容

（一）【实验题1】

1. 问题的求解算法及数据结构（流程图根据求解算法画）

复合梯形

给出积分区间(a,b)-->求h-->通过x=a+i*h求出x

-->求[f(a)+f(b)]/2-->sum累加-->得出h*sum即结果。

复合辛普森

给出积分区间(a,b)-->求h-->根据结点序号的奇偶性分别套公式求出S

-->S=(f(a)+S+f(b))*h/3。

龙贝格

给出积分区间(a,b)-->求h-->根据梯形公式求出t2-->

-->t1=t2,s1=s2,c1=c2,r1=r2,s=0-->利用公式分别求出

t2,s2,c2,r2-->n=2n-->h=h/2-->计算精度-->不满足则

继续以上操作-->直到满足精度要求则结束并且输出r2。

源程序清单

/*复合梯形*/
#include <stdio.h>
#include <math.h>
#define EPS 0.5e-7
// 定义被积函数
double f(double x) {
    return (-2.0/(x*x-1));
}
// 复合梯形公式
double trapezoidal(double a, double b, int n) {
    double h = (b - a) / n;//步长
    double sum = (f(a) + f(b)) / 2.0;    
	for (int i = 1; i < n; i++) {
	    double x = a + i * h;        
		sum += f(x);    
	}    
	return h * sum;
}
int main() {
    double a = 2, b = 3; // 积分区间
    int n = 20; // 将区间分为n个小区间    
	double result = trapezoidal(a, b, n);   
//输出近似解 
	printf("The result is: %lf\n", result);   
//输出精确解
	printf("The exact value is %lf", log(2)-log(3));
	return 0;
}

/*复合Simpson*/
#include <stdio.h>
#include <math.h>
#define EPS 0.5e-7
// 定义被积函数
double f(double x) {
    return (-2.0/(x*x-1));
}
// 复合Simpson公式
double simpson(double a, double b, int n) {
    double h = (b - a) / n;
    double sum = f(a) + f(b);    
	for (int i = 1; i < n; i++) {
        double x = a + i * h;
        if (i % 2 == 0) {            
			sum += 2.0 * f(x);
        } else {
            sum += 4.0 * f(x);        
		}
    }
    return h * sum / 3.0;
}
int main() {
    double a = 2,b = 3; // 积分区间 
	int n = 20; // 将区间分为n个小区间    
	double result = simpson(a, b, n);    
//输出近似解 
	printf("The result is: %lf\n", result);   
//输出精确解
	printf("The exact value is %lf", log(2)-log(3));  
	return 0;
}

/*龙贝格*/
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define EPS 0.5e-7
double f(double x)
{
    double f1;
    if(x != 0) f1=(-2.0 / (x*x-1));
    return f1;
}
void rom(double a, double b)
{
    double h, s1, c1, r1, s2, c2, r2, t1, t2, s;
    int i, k, n;
    h=(b - a) / 2;
    t2=(f(a) + f(b)) * h;
    s2 = 0;
    c2 = 0;
    r2 = 0;
    n = 1;
    k = 0;
    do{
//循环求r2
        t1 = t2;
        s1 = s2;
        c1 = c2;
        r1 = r2;
        s = 0.0;
        for(i = 1; i <= n; i++)
        {
            s = s + f(a + (2*i - 1) * h);
        }
//分别计算t2,s2,c2,r2（套公式）
        t2 = t1/2 + s*h;
        s2 = (4*t2 - t1) / 3;
        c2 = (16*s2 - s1) / 15;
        r2 = (64*c2 - c1) / 63;
        n = n*2;
        k = k+1;
        h = h/2;
//输出近似解
        printf("R(%d) = %.9lf\n", k, r2);
          
    }while(fabs(r2-r1) >= EPS);
//输出精确解
	 printf("\nThe exact value is %lf", log(2)-log(3));
}
 
int main()
{
    double a, b;//积分区间
    a=2;
    b=3;
    rom(a, b);
}

程序运行结果及分析

结果：

复合梯形：

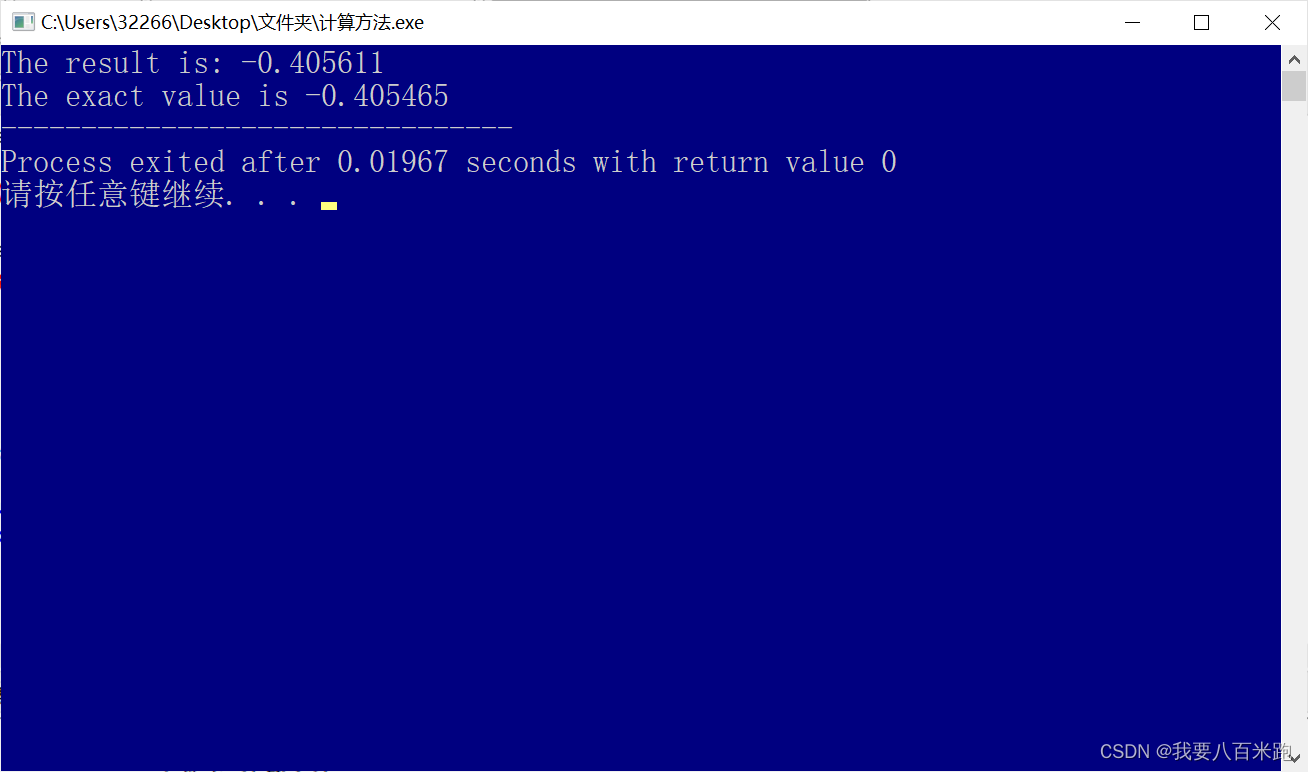
复合辛普森：

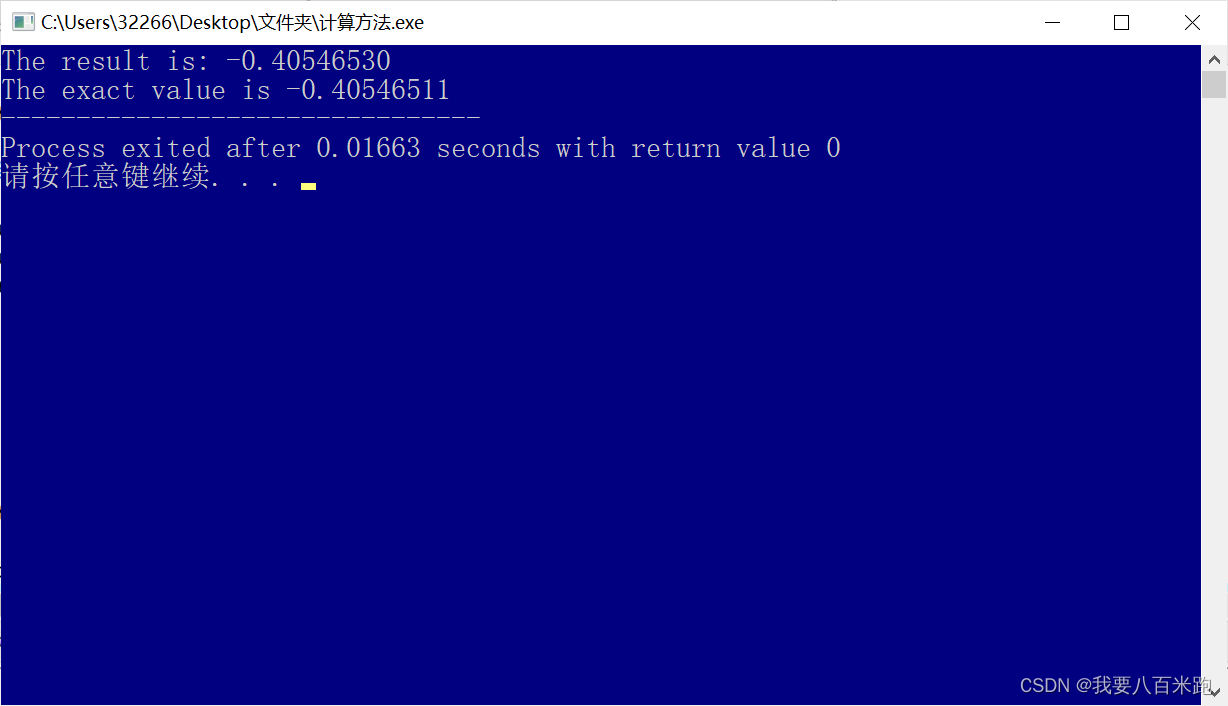
龙贝格：

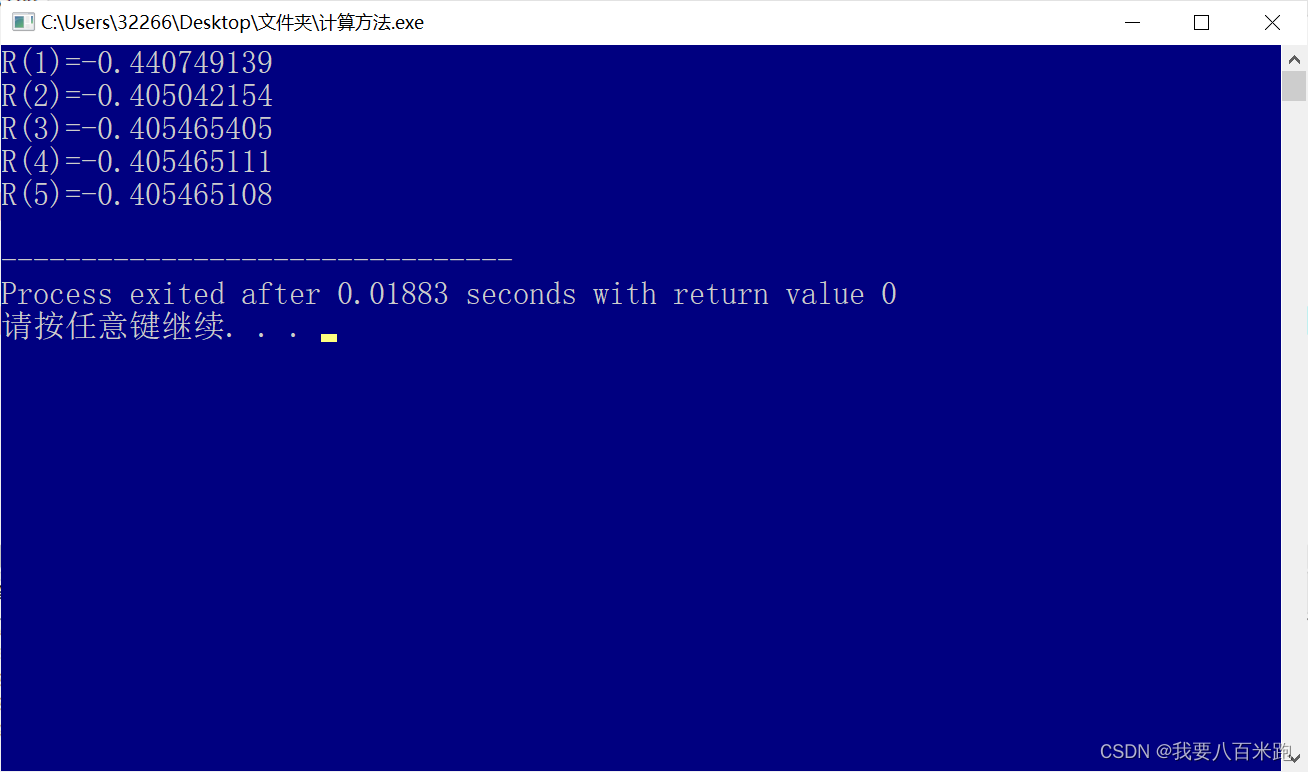
分析：

从结果可以看出，复合梯形公式的收敛速度较慢，复合梯形和复合辛普森方法里，都将积分区间分成20份，复合梯形公式只有三位有效精确数字，复合Simpson精确到了6位，它的收敛速度更快。如果按照精度来对照的话，T(512)才能计算出和精确值有6位有效数，而S（32）就能得到此结果，也可以看出复合梯形的收敛速度更慢。而龙贝格的精度在它们两之上，收敛速度也可以从结果看出很快。

实验总结

在本次实验中，我掌握了复合梯形公式、复合辛普森公式以及龙贝格公式的基本算法和思想，通过编程来实现用复合梯形公式、复合辛普森公式以及龙贝格公式求积分。而且通过上机实验，可以看到复合辛普森公式和龙贝格公式得到的结果更加精确，收敛速度更快。同时对编码能力也有在提高，对其中常用语句运用更自如。