第二章:导数与微分
第一节:导数的概念
导数其实表示的是一种极限,根据导数的定义可以把导数题转换称极限题去做。斜率不是导数,斜率只是导数的一种表现形式
基本概念
-
f ( x ) f(x) f(x)在 x 0 x_0 x0处可导的定义: y = f ( x ) y = f(x) y=f(x)在点 x 0 x_0 x0的某领域内有定义,若 lim Δ → 0 Δ y Δ x = lim Δ → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x \lim_{\Delta \to 0}{\frac{\Delta y}{\Delta x}} = \lim_{\Delta \to 0}{\frac{f(x_0 + \Delta x)-f(x_0)}{\Delta x}} limΔ→0ΔxΔy=limΔ→0Δxf(x0+Δx)−f(x0)存在,则称函数 f ( x ) f(x) f(x)在点 x 0 x_0 x0处可导,并称次极限为 y = f ( x ) y = f(x) y=f(x)在点 x 0 x_0 x0处的导数。记作 y ′ ∣ x = x 0 ; f ′ ( x 0 ) y^{'}\vert_{x =x_0};f^{'}(x_0) y′∣x=x0;f′(x0); d y d x ∣ x = x 0 \frac{dy}{dx}\vert_{x=x_0} dxdy∣x=x0; d f ( x ) d x ∣ x = x 0 \frac{df(x)}{dx}\vert_{x=x_0} dxdf(x)∣x=x0即: y ′ ∣ x = x 0 = f ′ ( x ) = lim Δ x → 0 Δ y Δ x = lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x = lim h → 0 f ( x 0 + h ) − f ( x 0 ) h y^{'}\vert_{x=x_0}= f^{'}(x) = \lim_{\Delta x \to 0}{\frac{\Delta y}{\Delta x}}= \lim_{\Delta x \to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} = \lim_{h \to 0}{\frac{f(x_0+h)-f(x_0)}{h}} y′∣x=x0=f′(x)=limΔx→0ΔxΔy=limΔx→0Δxf(x0+Δx)−f(x0)=limh→0hf(x0+h)−f(x0)
-
在 f ( x ) f(x) f(x)在 x 0 x_0 x0处可导的定义中, Δ \Delta Δ可以为 2 Δ 2\Delta 2Δ, n Δ n\Delta nΔ,但不能为 Δ 2 \Delta^2 Δ2,因为 Δ 2 \Delta^2 Δ2只能取到 0 + 0^+ 0+,但是取不到 0 − 0^- 0−,而 Δ \Delta Δ必须包括 0 − 0^- 0−和 0 + 0^+ 0+
-
单侧导数定义:设函数 y = f ( x ) y = f(x) y=f(x)在点 x 0 x_0 x0处存在如下单侧极限 lim x → 0 − Δ y Δ x = lim x → 0 − f ( x 0 + Δ x ) − f ( x 0 ) Δ x \lim_{x \to 0^-}{\frac{\Delta y}{\Delta x}} = \lim_{x \to 0^-}{\frac{f(x_0 + \Delta x)-f(x_0)}{\Delta x}} limx→0−ΔxΔy=limx→0−Δxf(x0+Δx)−f(x0), lim Δ x → 0 + Δ y Δ x = lim Δ x → 0 + f ( x 0 + Δ x ) − f ( x 0 ) Δ x \lim_{\Delta x \to 0^+}{\frac{\Delta y}{\Delta x}} = \lim_{\Delta x \to 0^+}{\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}} limΔx→0+ΔxΔy=limΔx→0+Δxf(x0+Δx)−f(x0)则分别称 f ( x ) f(x) f(x)在 x = x 0 x = x_0 x=x0处左,右可导,上述极限值分别称为 f ( x ) f(x) f(x)在 x = x 0 x= x_0 x=x0处的左,右导数,记为 f − ′ ( x 0 ) , f + ′ ( x 0 ) 或 y − ′ ( x 0 ) , y + ′ ( x 0 ) f^{'}_{-}(x_0),f_{+}^{'}(x_0)或y_{-}^{'}(x_0),y_{+}^{'}(x_0) f−′(x0),f+′(x0)或y−′(x0),y+′(x0)
-
导数的等价意义: 令 x = x 0 + Δ x 令x = x_0 +\Delta x 令x=x0+Δx,导数可以改写成 f ′ ( x 0 ) = lim x → x 0 f ( x ) − f ( x 0 ) x − x 0 f^{'}(x_0)= \lim\limits_{x \to x_0}{\frac{f(x)-f(x_0)}{x-x_0}} f′(x0)=x→x0limx−x0f(x)−f(x0)
- 注意:导数定义中, Δ x → 0 \Delta x \to 0 Δx→0一定包含 Δ x → 0 − \Delta x \to 0^- Δx→0−以及 Δ x → 0 + \Delta x \to 0^+ Δx→0+(或 x → x 0 − , x → x 0 + x \to x_0^-,x \to x_0^+ x→x0−,x→x0+)
-
f ( x ) f(x) f(x)在 ( a , b ) (a,b) (a,b)内可导的定义:若 f ( x ) f(x) f(x)在 ( a , b ) (a,b) (a,b)内逐点可导,则称 f ( x ) f(x) f(x)在开区间 ( a , b ) (a,b) (a,b)内可导
-
f ( x ) f(x) f(x)在 [ a , b ] [a,b] [a,b]内可导的定义:若 f ( x ) f(x) f(x)在 ( a , b ) (a,b) (a,b)内逐点可导,则称 f ( x ) f(x) f(x)在开区间 ( a , b ) (a,b) (a,b)内可导,若 f ( x ) f(x) f(x)在 ( a , b ) (a,b) (a,b)内可导,且 f ( x ) f(x) f(x)在 x = a x = a x=a处右可导,在 x = b x =b x=b处左可导,则称 f ( x ) f(x) f(x)在闭区间 [ a , b ] [a,b] [a,b]上可导。记为 f ( x ) ∈ D [ a , b ] f(x)\in D[a,b] f(x)∈D[a,b]或 f ( x ) ∈ C 2 [ a , b ] f(x)\in C_2[a,b] f(x)∈C2[a,b]
重要公式
- 椭圆方程的切线公式
- 椭圆 x 2 a 2 + y 2 b 2 = 1 \frac{x^2}{a^2}+\frac{y^2}{b^2} = 1 a2x2+b2y2=1,在 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)处的切线方程: x ⋅ x 0 a 2 + y ⋅ y 0 b 2 = 1 \frac{x\cdot x_0}{a^2}+\frac{y\cdot y_0}{b^2} = 1 a2x⋅x0+b2y⋅y0=1
- 椭球面 x 2 a 2 + y 2 b 2 + z 2 c 2 = 1 \frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}= 1 a2x2+b2y2+c2z2=1在 ( x 0 , y 0 , z 0 ) (x_0,y_0,z_0) (x0,y0,z0)处的切平面: x x 0 a 2 + y y 0 b 2 + z z 0 c 2 = 1 \frac{xx_0}{a^2}+\frac{yy_0}{b^2}+\frac{zz_0}{c^2}= 1 a2xx0+b2yy0+c2zz0=1
- 例题:
- x 2 + y 2 4 = 1 在 ( 3 2 , 1 ) x^2+\frac{y^2}{4} = 1在(\frac{\sqrt{3}}{2},1) x2+4y2=1在(23,1)处切线方程
- 函数
y
y
y在点
(
x
0
,
y
0
)
(x_0,y_0)
(x0,y0)处的切线方程和法线方程
-
切线方程: y − y 0 = f ′ ( x 0 ) ( x − x 0 ) y-y_0 = f^{'}(x_0)(x-x_0) y−y0=f′(x0)(x−x0)
-
法线方程: y − y 0 = − 1 f ′ ( x 0 ) ( x − x 0 ) , ( f ′ ( x 0 ) ≠ 0 ) y - y_0 = -\frac{1}{f^{'}{(x_0)}}(x-x_0) ,(f^{'}(x_0)\neq 0) y−y0=−f′(x0)1(x−x0),(f′(x0)=0)
-
重要性质
-
函数 y = f ( x ) y = f(x) y=f(x)在点 x 0 x_0 x0处可导的充要条件: f − ′ ( x 0 ) f_-^{'}(x_0) f−′(x0)与 f + ′ ( x 0 ) f_+^{'}(x_0) f+′(x0)都存在且相等
-
可导与连续关系: f ( x ) f(x) f(x)在点 x 0 x_0 x0处可导,则 f ( x ) f(x) f(x)在点 x 0 x_0 x0处连续,反之函数在点 x 0 x_0 x0处连续则未必可导。
-
导数的几何意义:
-
曲线 y = f ( x ) y = f(x) y=f(x)在点 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)处的切线的斜率为 t a n α = f ′ ( x 0 ) , 若 f ′ ( x 0 ) = 0 tan\alpha = f^{'}(x_0),若f^{'}(x_0) = 0 tanα=f′(x0),若f′(x0)=0,则切线与 x x x轴平行, x 0 x_0 x0称为驻点
-
f ′ ( x 0 ) ≠ ∞ f^{'}(x_0) \neq \infty f′(x0)=∞时,曲线在 ( x 0 , y 0 ) (x_0,y_0) (x0,y0)处
-
切线方程: y − y 0 = f ′ ( x 0 ) ( x − x 0 ) y-y_0 = f^{'}(x_0)(x-x_0) y−y0=f′(x0)(x−x0)
-
法线方程: y − y 0 = − 1 f ′ ( x 0 ) ( x − x 0 ) , ( f ′ ( x 0 ) ≠ 0 ) y - y_0 = -\frac{1}{f^{'}{(x_0)}}(x-x_0) ,(f^{'}(x_0)\neq 0) y−y0=−f′(x0)1(x−x0),(f′(x0)=0)
-
-
例题:
- 求 y = s i n 2 x 求y = sin^2x 求y=sin2x在 x = π 4 x = \frac{\pi}{4} x=4π 处的切线方程
- 设曲线 y = l n x y = lnx y=lnx与 y = a x y = a\sqrt{x} y=ax相切,求公切线。
-
-
导数的物理意义:一阶导表示速度,二阶导表示加速度。
-
求两曲线相切的切点的公切线:切点满足两个特点,切点处函数值相等和切点处切线斜率(导数)相等
解题思路
-
导数可导的等价关系(函数 y = f ( x ) y = f(x) y=f(x)在点 x 0 x_0 x0处可导的充要条件: f − ′ ( x 0 ) f_-^{'}(x_0) f−′(x0)与 f + ′ ( x 0 ) f_+^{'}(x_0) f+′(x0)都存在且相等)的应用:
- 方法:
- 证明一个函数是否可导,就一个方法,就是判断 f − ′ ( x 0 ) 与 f + ′ ( x 0 ) 是否都存在且相等 f_-^{'}(x_0)与f_+^{'}(x_0)是否都存在且相等 f−′(x0)与f+′(x0)是否都存在且相等
- 如果说一个函数在一点 x 0 x_0 x0可导,也可以知道 f − ′ ( x 0 ) = f + ′ ( x 0 ) f_-^{'}(x_0)=f_+^{'}(x_0) f−′(x0)=f+′(x0)
- 例题:
- 证明函数 f ( x ) = ∣ x ∣ f(x) = |x| f(x)=∣x∣在 x = 0 x = 0 x=0不可导
- 方法:
-
导数定义的应用:凑定义式,分子,一动一定,分母,上下一致。
-
导数定义所能解决的问题:
- 利用导数定义求极限:抽象函数,隐函数
- 利用导数定义求导数:抽象函数,分段函数,复杂函数
- 利用导数定义求是否可导: f − ′ ( x 0 ) f_-^{'}(x_0) f−′(x0)与 f + ′ ( x 0 ) f_+^{'}(x_0) f+′(x0)都存在且相等和函数可导是互为充要条件
-
例题:
-
f ( x ) f(x) f(x)可导且为奇函数, f ′ ( − 1 ) = 2 f^{'}(-1) = 2 f′(−1)=2,求 lim x → 0 f ( 1 + 3 x ) + f ( − 1 + x ) x \lim\limits_{x\to 0}\frac{f(1+3x)+f(-1+x)}{x} x→0limxf(1+3x)+f(−1+x)
-
f ′ ( 0 ) = 2 f^{'}(0) = 2 f′(0)=2存在,求极限 lim x → 0 f ( 2 x ) − f ( x ) x \lim\limits_{x\to 0}\frac{f(2x)-f(x)}{x} x→0limxf(2x)−f(x)
-
设 f ( x ) f(x) f(x)在 x = 2 x = 2 x=2处可导,且 lim x → 2 f ( x ) − 2 x 2 − 4 = 2 \lim\limits_{x\to 2}\frac{f(x)-2}{x^2-4} = 2 x→2limx2−4f(x)−2=2,求 f ( 2 ) f(2) f(2), f ′ ( 2 ) f^{'}(2) f′(2)(提示: f ( x ) f(x) f(x)可导,说明 f ( x ) f(x) f(x)连续, lim x → 2 x 2 − 4 = 0 \lim_{x \to 2}x^2-4 = 0 limx→2x2−4=0,则一个极限除一个极限等于 0 0 0的极限等于常数,则这个极限也等于 0 0 0)
-
设 f ( 0 ) = 0 f(0) = 0 f(0)=0, lim x → 0 1 x 2 f ( 1 − e x ) \lim\limits_{x\to 0}\frac{1}{x^2}f(1-e^x) x→0limx21f(1−ex)存在,求 f ′ ( 0 ) f^{'}(0) f′(0)
-
已知 f ( x ) = x ( x − 1 ) ( x − 2 ) … … ( x − 99 ) , f ′ ( 0 ) f(x) = x(x-1)(x-2)……(x-99),f^{'}(0) f(x)=x(x−1)(x−2)……(x−99),f′(0)
-
证明函数 f ( x ) = ∣ x ∣ f(x) = |x| f(x)=∣x∣在 x = 0 x = 0 x=0不可导
-
设 f ( 0 ) = 0 f(0) = 0 f(0)=0,则 f ( x ) f(x) f(x)在 x = 0 x = 0 x=0处可导的充要条件是()
A. lim h → 0 1 h 2 f ( 1 − c o s h ) \lim\limits_{h \to 0}\frac{1}{h^2}f(1-cosh) h→0limh21f(1−cosh)存在,B. lim h → 0 1 h f ( 1 − e h ) \lim\limits_{h \to 0}\frac{1}{h}f(1-e^h) h→0limh1f(1−eh)存在
C. lim h → 0 1 h 2 f ( h − s i n h ) \lim\limits_{h \to 0}\frac{1}{h^2}f(h-sinh) h→0limh21f(h−sinh)存在,C. lim h → 0 f ( 2 h ) − f ( h ) h \lim\limits_{h\to 0}\frac{f(2h)-f(h)}{h} h→0limhf(2h)−f(h)存在
-
-
第二节:函数的求导法则
基本概念
- 函数的类型:复合函数,反函数,隐函数,幂指函数,分段函数,参数方程确定的函数,变限积分函数。
重要公式
-
基本求导公式(正着逆着都要熟练掌握,考试的时候这个会变着样子考,很重要)
( x a ) ′ = a x a − 1 ( a x ) ′ = a x l n x , ( e x ) ′ = e x ( l o g a x ) ′ = 1 x l n a , ( l n x ) ′ = 1 x , ( l n ∣ x ∣ ) ′ = 1 x ( s i n x ) ′ = c o s x , ( c o s x ) ′ = − s i n x ( t a n x ) ′ = s e c 2 x , ( c o t x ) ′ = − c s c 2 x ( s e c x ) ′ = s e c x t a n x , ( c s c x ) ′ = − c s c x c o t x ( a r c s i n x ) ′ = 1 1 − x 2 , ( a r c c o s x ) ′ = − 1 1 − x 2 ( a r c t a n x ) ′ = 1 1 + x 2 , ( a r c c o t x ) ′ = − 1 1 + x 2 (x^a)^{'} = ax^{a-1}\\ (a^x)^{'} = a^xlnx , (e^x)^{'} = e^x\\ (log_ax)^{'} = \frac{1}{xlna}, (lnx)^{'} = \frac{1}{x} ,(ln|x|)^{'} = \frac{1}{x}\\ (sinx)^{'} = cosx , (cosx)^{'} = -sinx\\ (tanx)^{'} = sec^2x , (cotx)^{'} = -csc^2x\\ (secx)^{'} = secxtanx , (cscx)^{'} = -cscxcotx\\ (arcsinx)^{'} = \frac{1}{\sqrt {1-x^2}} , (arccosx)^{'} = -\frac{1}{\sqrt {1-x^2}}\\ (arctanx)^{'} = \frac{1}{1+x^2} ,(arccotx)^{'} = -\frac{1}{1+x^2}\\ (xa)′=axa−1(ax)′=axlnx,(ex)′=ex(logax)′=xlna1,(lnx)′=x1,(ln∣x∣)′=x1(sinx)′=cosx,(cosx)′=−sinx(tanx)′=sec2x,(cotx)′=−csc2x(secx)′=secxtanx,(cscx)′=−cscxcotx(arcsinx)′=1−x21,(arccosx)′=−1−x21(arctanx)′=1+x21,(arccotx)′=−1+x21 -
导数四则运算
-
( u ± v ) ′ = u ′ + v ′ (u \pm v)^{'} = u^{'}+v{'} (u±v)′=u′+v′
-
( k u ) ′ = k u ′ (ku)^{'} = ku^{'} (ku)′=ku′
-
( u v ) ′ = u ′ v + u v ′ , ( u v w ) ′ = u ′ v w + u v ′ w + u v w ′ (uv)^{'} = u^{'}v+uv^{'},(uvw)^{'}= u^{'}vw+uv^{'}w+uvw^{'} (uv)′=u′v+uv′,(uvw)′=u′vw+uv′w+uvw′
-
( u v ) ′ = u ′ v − u v ′ v 2 , ( v ≠ 0 ) (\frac{u}{v})^{'}= \frac{u^{'}v-uv^{'}}{v^2},(v\neq 0) (vu)′=v2u′v−uv′,(v=0)
-
-
极坐标化直角坐标公式:
- x = r c o s θ = r ( θ ) c o s θ x = rcos\theta = r(\theta)cos\theta x=rcosθ=r(θ)cosθ
- y = r s i n θ = r ( θ ) s i n θ y = rsin\theta = r(\theta)sin\theta y=rsinθ=r(θ)sinθ
-
C m n C^n_m Cmn求解公式: n ( n − 1 ) . . . ( n − m + 1 ) m ! \frac{n(n-1)...(n-m+1)}{m!} m!n(n−1)...(n−m+1)
-
反函数的求导公式:
-
设 f ( x ) f(x) f(x)可导,且 f ′ ( x ) ≠ 0 f^{'}(x)\neq 0 f′(x)=0,又设 x = φ ( y ) x = \varphi(y) x=φ(y)为 y = f ( x ) y = f(x) y=f(x)的反函数,则 φ ′ ( y ) = d x d y = 1 d y d x = 1 f ′ ( x ) \varphi^{'}(y) = \frac{dx}{dy} = \frac{1}{\frac{dy}{dx}} = \frac{1}{f^{'}(x)} φ′(y)=dydx=dxdy1=f′(x)1。
-
设 f ( x ) f(x) f(x)二阶可导,且 f ′ ( x ) ≠ 0 f^{'}(x) \neq 0 f′(x)=0,又设 x = φ ( y ) x = \varphi(y) x=φ(y)为 y = f ( x ) y = f(x) y=f(x)反函数,则 φ ′ ′ ( y ) = − f ′ ′ ( x ) f ′ 3 ( x ) \varphi^{''}(y) = -\frac{f^{''}(x)}{f^{'3}(x)} φ′′(y)=−f′3(x)f′′(x)
-
重要性质
-
复合函数的求导法则: y = f ( u ) y = f(u) y=f(u)可导, u = φ ( x ) u= \varphi(x) u=φ(x)可导,则 f [ φ ( x ) ] f[\varphi(x)] f[φ(x)]也可导,且 d y d x = f [ φ ( x ) ] φ ′ ( x ) \frac{dy}{dx} = f[\varphi(x)]\varphi^{'}(x) dxdy=f[φ(x)]φ′(x)
-
反函数的求导法则:
- 定理一: 设 f ( x ) 可导,且 f ′ ( x ) ≠ 0 , 又设 x = φ ( y ) 为 y = f ( x ) 的反函数,则 φ ′ ( y ) = d x d y = 1 d y d x = 1 f ′ ( x ) 。 设f(x)可导,且f^{'}(x)\neq 0,又设x = \varphi(y)为y = f(x)的反函数,则\varphi^{'}(y) = \frac{dx}{dy} = \frac{1}{\frac{dy}{dx}} = \frac{1}{f^{'}(x)}。 设f(x)可导,且f′(x)=0,又设x=φ(y)为y=f(x)的反函数,则φ′(y)=dydx=dxdy1=f′(x)1。
- 定理二:设 f ( x ) f(x) f(x)二阶可导,且 f ′ ( x ) ≠ 0 f^{'}(x) \neq 0 f′(x)=0,又设 x = φ ( y ) x = \varphi(y) x=φ(y)为 y = f ( x ) y = f(x) y=f(x)反函数,则 φ ′ ′ ( y ) = − f ′ ′ ( x ) f ′ 3 ( x ) \varphi^{''}(y) = -\frac{f^{''}(x)}{f^{'3}(x)} φ′′(y)=−f′3(x)f′′(x)
-
隐函数的导数:两边对 x x x求导,碰到 y y y,先对 y y y求导,再乘 y ′ y^{'} y′。碰到 y ′ y^{'} y′,先对 y ′ y^{'} y′求导,再乘 y ′ ′ y{''} y′′
-
由参数方程确定的函数的导数:设 y = f ( x ) 由 { x = φ ( x ) y = ψ ( x ) y = f(x)由\begin{cases}x = \varphi(x) \\ y = \psi(x)\end{cases} y=f(x)由{x=φ(x)y=ψ(x)确定, ψ ( t ) 二阶可导且 φ ′ ( x ) ≠ 0 , 则 \psi(t)二阶可导且\varphi^{'}(x) \neq 0,则 ψ(t)二阶可导且φ′(x)=0,则
- y ′ = d y d x = d y / d t d x / d t = ψ ′ ( t ) φ ′ ( t ) 。 y^{'} = \frac{dy}{dx} = \frac{dy/dt}{dx/dt} = \frac{\psi^{'}(t)}{\varphi^{'}(t)}。 y′=dxdy=dx/dtdy/dt=φ′(t)ψ′(t)。
- y ′ ′ = d y ′ / d t d x / d t y^{''} = \frac{dy^{'}/dt}{dx/dt} y′′=dx/dtdy′/dt
- 注意:参数方程中的单调区间指的是 x x x的范围。
-
幂指函数求导
- 法一: y = u ( x ) v ( x ) = e v ( x ) ln u ( x ) y = u(x)^{v(x)} = e^{v(x)\ln u(x)} y=u(x)v(x)=ev(x)lnu(x)
- 法二:
ln
y
=
v
(
x
)
ln
u
(
x
)
\ln y = v(x) \ln u(x)
lny=v(x)lnu(x),其他使用场景:
- 用于连乘或连除形式的函数求导(把乘除换成加减的形式)
- 用于幂函数或指数函数的求导(把幂函数或指数函数换成乘法的形式)。
-
分段函数求导方法:
- 分段点用导数定义来求
- 其他部分用求导法则
- 注意绝对值也是一种分段函数。
-
极坐标求导:
- step1:先化为直角坐标: x = r c o s θ = r ( θ ) c o s θ , y = r s i n θ = r ( θ ) s i n θ x = rcos\theta = r(\theta)cos\theta,y = rsin\theta = r(\theta)sin\theta x=rcosθ=r(θ)cosθ,y=rsinθ=r(θ)sinθ
- step2:得到一个参数方程,再使用参数方程的求导方法求导。
-
变限积分函数的求导法则
- [ ∫ a φ ( x ) f ( t ) d t ] ′ = f [ φ ( x ) ] φ ′ ( x ) [\int_a^{\varphi(x)} f(t)dt]^{'} = f[\varphi(x)]\varphi^{'}(x) [∫aφ(x)f(t)dt]′=f[φ(x)]φ′(x)
- [ ∫ ψ ( x ) φ ( x ) f ( t ) d t ] ′ = f [ φ ( x ) ] φ ′ ( x ) − f [ ψ ( x ) ] ψ ′ ( x ) [\int_{\psi(x)}^{\varphi(x)}f(t)dt]^{'} = f[\varphi(x)]\varphi^{'}(x)-f[\psi(x)]\psi^{'}(x) [∫ψ(x)φ(x)f(t)dt]′=f[φ(x)]φ′(x)−f[ψ(x)]ψ′(x)
- [ ∫ ψ ( x ) φ ( x ) g ( x ) f ( t ) d t ] ′ = [ g ( x ) ∫ ψ ( x ) φ ( x ) f ( t ) d t ] ′ = g ′ ( x ) ∫ ψ ( x ) φ ( x ) f ( t ) d t + g ( x ) { f [ φ ( x ) ] φ ′ ( x ) − f [ ψ ( x ) ] ψ ′ ( x ) } [\int_{\psi(x)}^{\varphi(x)}g(x)f(t)dt]^{'} = [g(x)\int_{\psi(x)}^{\varphi(x)}f(t)dt]^{'} = g^{'}(x)\int^{\varphi(x)}_{\psi(x)} f(t)dt+g(x)\{f[\varphi(x)]\varphi^{'}(x)-f[\psi(x)]\psi^{'}(x)\} [∫ψ(x)φ(x)g(x)f(t)dt]′=[g(x)∫ψ(x)φ(x)f(t)dt]′=g′(x)∫ψ(x)φ(x)f(t)dt+g(x){f[φ(x)]φ′(x)−f[ψ(x)]ψ′(x)}
- 使用上面三个法则求导前 f ( t ) f(t) f(t)中不能含有变量 x x x
解题思路
-
求不可导点步骤
- 步骤:
- 第一步:找可疑点:分段点,绝对值等于零的点。
- 第二步:用导数定义判断点是否可导
- 做小题时,如果函数图像可以画出来,可以看函数图像的点是否光滑,不光滑的点就是不可导点。
- 例题:
- 设函数 f ( x ) = lim x → ∞ 1 + ∣ x ∣ 3 n n , 求 f ( x ) 在 ( − ∞ , + ∞ ) 内不可导的点 设函数f(x) = \lim\limits_{x\to \infty}\sqrt[n]{1+|x|^{3n}},求f(x)在(-\infty,+\infty)内不可导的点 设函数f(x)=x→∞limn1+∣x∣3n,求f(x)在(−∞,+∞)内不可导的点
- 步骤:
-
七大函数的求导
-
步骤:
- step1:确定函数类型和函数定义域。
- step2:分类求导
-
例题:
- y = e s i n 1 x y = e^{sin\frac{1}{x}} y=esinx1,求 d y d x \frac{dy}{dx} dxdy
- 设 y = x a a + a x a + a a x y = x^{a^a}+a^{x^a}+a^{a^x} y=xaa+axa+aax,求 y ′ y^{'} y′
- y = f ( x ) y = f(x) y=f(x)的反函数 x = g ( y ) x = g(y) x=g(y), f ( 2 ) = 1 f(2) = 1 f(2)=1, f ′ ( 2 ) = 3 f^{'}(2) = 3 f′(2)=3,求 g ′ ( 1 ) g^{'}(1) g′(1)
- 设 f ( x ) f(x) f(x)可导, φ ( x ) \varphi(x) φ(x)为 f ( x ) f(x) f(x)的反函数,且 f ( 2 ) = 4 , f ′ ( 2 ) = 5 f(2) = 4,f^{'}(2) = \sqrt{5} f(2)=4,f′(2)=5, f ′ ( 4 ) = 6 f^{'}(4) = \sqrt{6} f′(4)=6,求 φ ′ ( 4 ) \varphi^{'}(4) φ′(4)
- f ( x ) f(x) f(x)可导, x = φ ( y ) x = \varphi(y) x=φ(y)为 y = f ( x ) y = f(x) y=f(x)的反函数, f ′ ( x ) = e x 2 + x + 1 f^{'}(x) = e^{x^2+x+1} f′(x)=ex2+x+1, f ( 0 ) = 3 f(0) = 3 f(0)=3,求 φ ′ ( 3 ) \varphi^{'}(3) φ′(3)
- y 5 + 2 y − x − 3 x 7 = 0 y^5+2y-x-3x^7 = 0 y5+2y−x−3x7=0,求 y ′ ( 0 ) , y ′ ′ ( 0 ) y^{'}(0),y^{''}(0) y′(0),y′′(0)
- 设 { x = f ′ ( t ) y = t f ′ ( t ) − f ( t ) \begin{cases}x = f^{'}(t)\\y = tf^{'}(t)-f(t)\end{cases} {x=f′(t)y=tf′(t)−f(t),求 d x d y \frac{dx}{dy} dydx
- 设 { x = 3 t 2 + 2 t e y s i n t − y + 1 = 0 \begin{cases}x = 3t^2+2t\\e^ysint-y+1 = 0\end{cases} {x=3t2+2teysint−y+1=0确定 y = y ( x ) y = y(x) y=y(x)函数,求 d y d x ∣ t = 0 \frac{dy}{dx}|_{t = 0} dxdy∣t=0
- F ( x ) = ∫ c o s x 1 e − t 2 d t F(x) = \int^{1}_{cosx}e^{-t^2}dt F(x)=∫cosx1e−t2dt,求 F ′ ( x ) F^{'}(x) F′(x)
- f ( x ) = ∫ 0 x s i n ( x − t ) 2 d t f(x) = \int^x_0sin(x-t)^2dt f(x)=∫0xsin(x−t)2dt,求 f ′ ( x ) f^{'}(x) f′(x)(第六章会讲)
- 求 lim x → 0 ∫ 0 x s i n ( x − t ) 2 d t x − s i n x \lim\limits_{x\to 0}\frac{\int^x_0sin(x-t)^2dt}{x-sinx} x→0limx−sinx∫0xsin(x−t)2dt
- f ( x ) = { l n ( 1 + 2 x ) x > 0 2 x = 0 2 c o s x x < 0 f(x) = \begin{cases}ln(1+2x)&x>0\\ 2&x = 0\\2cosx &x<0\end{cases} f(x)=⎩ ⎨ ⎧ln(1+2x)22cosxx>0x=0x<0,求 f ′ ( x ) f^{'}(x) f′(x)
- y = ( x − 1 ) ( x + 1 ) 3 e x − 2 ⋅ ( x − 3 ) 4 , ( x > 3 ) y = \sqrt{\frac{(x-1)(x+1)^3}{e^{x-2}\cdot(x-3)^4}},(x>3) y=ex−2⋅(x−3)4(x−1)(x+1)3,(x>3),求 y ′ y^{'} y′
- x y = y x x^y = y^x xy=yx,求 d y d x \frac{dy}{dx} dxdy
- 设 y = x x y = x^x y=xx,求 y ′ y^{'} y′
- 求曲线 r = θ r = \theta r=θ,在点 ( r , θ ) = ( π 2 , π 2 ) (r,\theta) = (\frac{\pi}{2},\frac{\pi}{2}) (r,θ)=(2π,2π)处切线的直角方程
-
第三节:高阶导数
基本概念
- 高阶导定义:若函数 y = f ( x ) y = f(x) y=f(x)的导数 y ′ = f ′ ( x ) y^{'} = f^{'}(x) y′=f′(x)可导,则称 f ′ ( x ) f^{'}(x) f′(x)的导数为 f ( x ) f(x) f(x)的二阶导数,记作: y ′ ′ 或 d 2 y d x 2 y^{''}或\frac{d^2y}{dx^2} y′′或dx2d2y,即 y ′ ′ = ( y ′ ) ′ y^{''} = (y^{'})^{'} y′′=(y′)′或 d 2 y d x 2 = d d x ( d y d x ) \frac{d^2y}{dx^2} = \frac{d}{dx}(\frac{dy}{dx}) dx2d2y=dxd(dxdy),类似地,二阶导数的导数称为三阶导数,以此类推,分别记作: y ′ ′ , y ( 4 ) , . . . , y ( n ) y^{''},y^{(4)},...,y^{(n)} y′′,y(4),...,y(n),或, d 3 y d x 3 , d 4 y d x 4 , . . . , d n y d x n \frac{d^3y}{dx^3},\frac{d^4y}{dx^4},...,\frac{d^ny}{dx^n} dx3d3y,dx4d4y,...,dxndny
重要公式
- 常用的高阶导数
- { ( e k x ) ( n ) = k n e k x ( a k x ) ( n ) = ( k l n a ) n a k x \begin{cases}(e^{kx})^{(n)} = k^ne^{kx}\\(a^{kx})^{(n)} = (klna)^na^{kx}\end{cases} {(ekx)(n)=knekx(akx)(n)=(klna)nakx
- { [ s i n ( a x + b ) ] ( n ) = a n s i n ( a x + b + n π 2 ) [ c o s ( a x + b ) ] ( n ) = a n c o s ( a x + b + n π 2 ) \begin{cases}[sin(ax+b)]^{(n)} = a^n sin(ax+b+\frac{n\pi}{2})\\ [cos(ax+b)]^{(n)}=a^n cos(ax+b+\frac{n\pi}{2})\end{cases} {[sin(ax+b)](n)=ansin(ax+b+2nπ)[cos(ax+b)](n)=ancos(ax+b+2nπ)
- { ( 1 a x + b ) ( n ) = ( − 1 ) n n ! a n ( a x + b ) ( n + 1 ) [ l n ( a x + b ) ] ( n ) = ( − 1 ) n − 1 ( n − 1 ) ! a n ( a x + b ) n \begin{cases}(\frac{1}{ax+b})^{(n)} = \frac{(-1)^n n! a^n}{(ax+b)^{(n+1)}}\\ [ln(ax+b)]^{(n)} = \frac{(-1)^{n-1}(n-1)!a^n}{(ax+b)^n}\end{cases} {(ax+b1)(n)=(ax+b)(n+1)(−1)nn!an[ln(ax+b)](n)=(ax+b)n(−1)n−1(n−1)!an
重要性质
- 高阶导的运算法则
-
( u ± v ) ( n ) = u ( n ) ± v ( n ) (u\pm v)^{(n)} = u^{(n)}\pm v^{(n)} (u±v)(n)=u(n)±v(n)
-
( k u ) ( n ) = k u ( n ) (ku)^{(n)} = ku^{(n)} (ku)(n)=ku(n)
-
莱布尼茨公式: ( u v ) ( n ) = C n 0 u ( n ) v + C n 1 u ( n − 1 ) v ′ + . . . + C n n u v ( n ) (uv)^{(n)} = C^0_n u^{(n)}v+C^1_nu^{(n-1)}v^{'}+...+C^n_nuv^{(n)} (uv)(n)=Cn0u(n)v+Cn1u(n−1)v′+...+Cnnuv(n)
-
解题思路
- 高阶导求解
- 例题:
-
利用归纳法:
- y ′ , y ′ ′ , y ′ ′ ′ y^{'},y^{''},y^{'''} y′,y′′,y′′′,找规律。
- 遇到 s i n x + c o s x sinx+cosx sinx+cosx,要想到提取一个 2 \sqrt{2} 2,变成 2 s i n ( x + π 4 \sqrt{2}sin(x+\frac{\pi}{4} 2sin(x+4π)。
-
化为两个函数相加形式,使用 ( u ± v ) ( n ) = u ( n ) ± v ( n ) (u\pm v)^{(n)} = u^{(n)}\pm v^{(n)} (u±v)(n)=u(n)±v(n)
- 两种函数形式可以化为几个函数相加的形式
-
f ( x ) = l n ( a x 2 + b x + c ) f(x) = ln(ax^2+bx+c) f(x)=ln(ax2+bx+c)
-
f ( x ) = . . . a x 2 + b x + c f(x) = \frac{...}{ax^2+bx+c} f(x)=ax2+bx+c...,这种形式的函数当看不出如何转化为两式相加减的形式时,可以使用以下步骤:
-
第一步:化为,分母化为两式相乘的形式,例如 1 x 2 − 3 x + 2 化为 1 ( x − 2 ) ( x − 1 ) \frac{1}{x^2-3x+2}化为\frac{1}{(x-2)(x-1)} x2−3x+21化为(x−2)(x−1)1
-
第二步:设 1 ( x − 2 ) ( x − 1 ) = A x − 2 + B x − 1 \frac{1}{(x-2)(x-1)} = \frac{A}{x-2}+\frac{B}{x-1} (x−2)(x−1)1=x−2A+x−1B
-
第三步:通分 A x − 2 + B x − 1 = ( A + B ) x − A − 2 B ( x − 2 ) ( x − 1 ) \frac{A}{x-2}+\frac{B}{x-1} = \frac{(A+B)x-A-2B}{(x-2)(x-1)} x−2A+x−1B=(x−2)(x−1)(A+B)x−A−2B
-
第四步:解 { A + B = 0 − A − 2 B = 1 得, A = 1 , B = − 1 \begin{cases}A+B = 0\\-A-2B = 1\end{cases}得,A = 1,B = -1 {A+B=0−A−2B=1得,A=1,B=−1
-
-
- 两种函数形式可以化为几个函数相加的形式
-
利用莱布尼茨公式
- 公式: ( u v ) ( n ) = C n 0 u ( n ) v + C n 1 u ( n − 1 ) v ′ + . . . + C n n u v ( n ) (uv)^{(n)} = C^0_n u^{(n)}v+C^1_nu^{(n-1)}v^{'}+...+C^n_nuv^{(n)} (uv)(n)=Cn0u(n)v+Cn1u(n−1)v′+...+Cnnuv(n)
- 使用场景:两个函数相乘,函数的其中一项为幂函数 x n x^n xn,作为 v v v,随着 v v v的导数的阶数提高,最终会变成0,另一项为可归纳高阶导的函数,作为 u u u
-
- 例题:
- y = x 2 e 2 x , 求 y ( 20 ) y = x^2e^{2x},求y^{(20)} y=x2e2x,求y(20)
- 设函数 f ( x ) = x 2 s i n 3 x , 求 f ( 5 ) ( x ) 设函数f(x) = x^2sin3x,求f^{(5)}(x) 设函数f(x)=x2sin3x,求f(5)(x)
- 设 y = 1 x 2 − 3 x + 2 , 求 y ( n ) 设y = \frac{1}{x^2-3x+2},求y^{(n)} 设y=x2−3x+21,求y(n)
- y = 1 a x + b , 求 y ( n ) y = \frac{1}{ax+b},求y^{(n)} y=ax+b1,求y(n)
- y = e x s i n x , 求 y ( n ) y = e^xsinx,求y^{(n)} y=exsinx,求y(n)
- 设 f ( x ) 任意阶可导,且 f ′ ( x ) = [ f ( x ) ] 2 , 则当 n > = 2 时 , 求 f ( n ) ( x ) 设f(x)任意阶可导,且f^{'}(x) = [f(x)]^2,则当n>=2时,求f^{(n)}(x) 设f(x)任意阶可导,且f′(x)=[f(x)]2,则当n>=2时,求f(n)(x)
- y = s i n x c o s 2 x − s i n 3 x , 求 y ( n ) y = sinxcos^2x-sin^3x,求y^{(n)} y=sinxcos2x−sin3x,求y(n)
- 例题:
第四节:函数的微分
微分表示的是变化量, d y dy dy(微分)可以近似表示 Δ y \Delta y Δy
基本概念
-
函数的微分定义:若函数 y = f ( x ) y = f(x) y=f(x)在点 x 0 x_0 x0处的增量可表示为 Δ y = f ( x 0 + Δ x ) − f ( x 0 ) = A Δ x + o ( Δ x ) \Delta y = f(x_0+\Delta x)-f(x_0) = A\Delta x+o(\Delta x) Δy=f(x0+Δx)−f(x0)=AΔx+o(Δx),其中A为不依赖于 Δ x \Delta x Δx的常数,则称函数 y = f ( x ) y = f(x) y=f(x)在点 x 0 x_0 x0处可微,而 A Δ x A\Delta x AΔx称为 f ( x ) f(x) f(x)在点 x 0 x_0 x0处相应于自变量增量 Δ x \Delta x Δx的微分,记作 d y dy dy,即 d y = A d x . dy = Adx. dy=Adx.
-
这里需要注意,这里的 Δ x \Delta x Δx和 d x dx dx相等,但是 Δ y \Delta y Δy和 d y dy dy不一定相等,就比如: y = f ( x 2 ) y = f(x^2) y=f(x2)可导,取 x = − 1 x = -1 x=−1, Δ x = 0.01 \Delta x = 0.01 Δx=0.01, d y ∣ x = − 1 = − 0.5 dy|_{x = -1}=-0.5 dy∣x=−1=−0.5,求 f ′ ( 1 ) f^{'}(1) f′(1)。
-
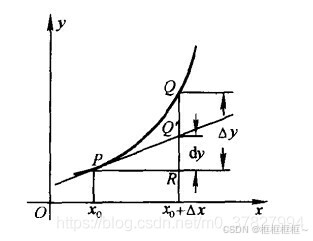
微分的几何意义:
-
d y dy dy:沿切线纵坐标的增量
-
Δ y \Delta y Δy:沿曲线纵坐标的增量
-
微分几何意义图:
-
重要公式
- d ( u ± v ) = d u ± d v d(u \pm v) = du \pm dv d(u±v)=du±dv
- d ( k u ) = k d u d(ku) = kdu d(ku)=kdu
- d ( u v ) = v d u + u d v d(uv) = vdu+udv d(uv)=vdu+udv
- d u v = v d u + u d v v 2 d\frac{u}{v} = \frac{vdu + udv}{v^2} dvu=v2vdu+udv
重要性质
-
微分的运算法则:
- d ( u ± v ) = d u ± d v d(u \pm v) = du \pm dv d(u±v)=du±dv
- d ( k u ) = k d u d(ku) = kdu d(ku)=kdu
- d ( u v ) = v d u + u d v d(uv) = vdu+udv d(uv)=vdu+udv
- d u v = v d u + u d v v 2 d\frac{u}{v} = \frac{vdu + udv}{v^2} dvu=v2vdu+udv
- 复合函数的微分(微分形式不变性):设 y = f ( u ) , u = φ ( x ) 都可导,则复合函数 y = f [ φ ( x ) ] y= f(u),u = \varphi(x)都可导,则复合函数y = f[\varphi(x)] y=f(u),u=φ(x)都可导,则复合函数y=f[φ(x)]的微分为 d y = y x ′ d x = f ′ ( u ) φ ′ ( x ) d x = f ′ ( u ) d u dy = y_x^{'}dx = f^{'}(u)\varphi^{'}(x)dx = f^{'}(u)du dy=yx′dx=f′(u)φ′(x)dx=f′(u)du
-
求微分等于求导: d f ( x ) = f ′ ( x ) d x df(x) = f^{'}(x)dx df(x)=f′(x)dx
-
凑微分等于积分,例如: 2 x d x = d ( x 2 + C ) , e s i n x c o s x d x = e s i n x d s i n x = d ( e s i n x + C ) 2xdx = d(x^2+C),e^{sinx}cosxdx = e^{sinx}dsinx = d(e^{sinx}+C) 2xdx=d(x2+C),esinxcosxdx=esinxdsinx=d(esinx+C)
解题思路
- 求复合函数微分:
- 运算法则:
- 设 y = f ( u ) , u = φ ( x ) y= f(u),u = \varphi(x) y=f(u),u=φ(x)都可导,则复合函数 y = f [ φ ( x ) ] y = f[\varphi(x)] y=f[φ(x)]的微分为 d y = y x ′ d x = f ′ ( u ) φ ′ ( x ) d x = f ′ ( u ) d u dy = y_x^{'}dx = f^{'}(u)\varphi^{'}(x)dx = f^{'}(u)du dy=yx′dx=f′(u)φ′(x)dx=f′(u)du
- d ( u ± v ) = d u ± d v d(u \pm v) = du \pm dv d(u±v)=du±dv
- d ( k u ) = k d u d(ku) = kdu d(ku)=kdu
- d ( u v ) = v d u + u d v d(uv) = vdu+udv d(uv)=vdu+udv
- d u v = v d u + u d v v 2 d\frac{u}{v} = \frac{vdu + udv}{v^2} dvu=v2vdu+udv
- 例题:
- 求 d e x + 2 y + 3 z de^{x+2y+3z} dex+2y+3z
- 运算法则:
y
=
f
(
u
)
,
u
=
φ
(
x
)
y= f(u),u = \varphi(x)
y=f(u),u=φ(x)都可导,则复合函数
y
=
f
[
φ
(
x
)
]
y = f[\varphi(x)]
y=f[φ(x)]的微分为
d
y
=
y
x
′
d
x
=
f
′
(
u
)
φ
′
(
x
)
d
x
=
f
′
(
u
)
d
u
dy = y_x^{'}dx = f^{'}(u)\varphi^{'}(x)dx = f^{'}(u)du
dy=yx′dx=f′(u)φ′(x)dx=f′(u)du
2.
d
(
u
±
v
)
=
d
u
±
d
v
d(u \pm v) = du \pm dv
d(u±v)=du±dv
3.
d
(
k
u
)
=
k
d
u
d(ku) = kdu
d(ku)=kdu
4.
d
(
u
v
)
=
v
d
u
+
u
d
v
d(uv) = vdu+udv
d(uv)=vdu+udv
5.
d
u
v
=
v
d
u
+
u
d
v
v
2
d\frac{u}{v} = \frac{vdu + udv}{v^2}
dvu=v2vdu+udv
2. 例题:
1. 求
d
e
x
+
2
y
+
3
z
de^{x+2y+3z}
dex+2y+3z

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








