文献分享: Muvera多向量到单向量的转化方法(Part1.导论/原理/实验)

$\text{1. }$导论与背景

$\text{1.1. }$研究背景

1️⃣两种文本相似性检索模型

类型	嵌入方式	相似度计算
单向量$\text{(SV)}$	对整个句子生成唯一的嵌入	$\text{MIPS}$算法，从一堆向量找出与$q$有最大内积的
多向量$\text{(MV)}$	对每个$\text{Token}$都生成一个嵌入	$\text{Chamfer}$相似度，也就是所谓的$\text{MaxSim}$之和

2️⃣多向量模型的问题：检索成本还是高过单向量

1. 空间占用上：$\text{Token}$数量过多，需要大量的存储
2. 计算成本上：缺乏对于$\text{Chamfer}$的优化，大多的优化只针对于$\text{MIPS}$而无法用在$\text{Chamfer}$上

3️⃣改进的尝试：将$\text{MV}$改为基于$\text{SV}$的$\text{MIPS}$流水(单向量启发式方法)

1. $\text{SV}$阶段：每个查询$\text{Token}\stackrel{\text{MIPS}}{\to }$最相似的文档$\text{Token}$
2. $\text{MV}$阶段：收集所有的最相似文档$\text{Token}$，再用原始$\text{Chamfer}$相似度得到最终评分

$\text{1.2. }$本文工作$\text{: Muvera}$概述

1️⃣$\text{Chamfer}$相似度

1. 相似度的定义：对查询$Q/$段落$P$的每个$\text{Token}(q/p)$，相似度为$\text{Chamfer}(Q,P)\text{=}\sum _{q\text{∈}Q}\underset{p\text{∈}P}{\max }⟨q,p⟩$
2. 扩展到最邻近：在$\mathcal{P}\text{=}\left\{P^{(1)},P^{(2)},\dots ,P^{(N)}\right\}$中找到与$Q$之间$\text{Chamfer}$相似度最高的文档$P^{\ast }\text{∈}D$

2️⃣$\text{Muvera}$概述

1. 核心思想：将所向量压缩为单向量，原有的$\text{Chamfer}$搜索也变成$\text{MIPS}$搜索
   • 维度压缩：特殊的映射函数$\{\begin{array}{l}{\mathbf{F}}_{\mathrm{que}}:2^{{\mathbb{R}}^d}\to {\mathbb{R}}^{d_{\mathrm{FDE}}}\\ \\ {\mathbf{F}}_{\text{doc}}:2^{{\mathbb{R}}^d}\to {\mathbb{R}}^{d_{\mathrm{FDE}}}\end{array}\text{→}$将多向量压缩为固定$d_{\text{FDE}}$维单向量编码
   • 相似度计算：用内积$⟨{\mathbf{F}}_{\mathrm{que}}(Q),{\mathbf{F}}_{\text{doc}}(P)⟩$作为原有$\text{Chamfer}(Q,P)\text{=}\sum _{q\text{∈}Q}\underset{p\text{∈}P}{\max }⟨q,p⟩$的替代
2. 工作流程：
   • 预处理：对所有文档进行${\mathbf{F}}_{\text{doc}}$映射得到${\mathbf{F}}_{\text{doc}}(P_i)$的固定维度编码($\text{FDEs}$)
   • 查询初排：对查询$Q$进行${\mathbf{F}}_{\text{que}}$映射得到${\mathbf{F}}_{\text{que}}(Q)$，计算$⟨{\mathbf{F}}_{\mathrm{que}}(Q),{\mathbf{F}}_{\text{doc}}(P_i)⟩$得到$\text{Top-}k$文档
   • 查询重排：再用完整的$\sum _{q\in Q}\underset{p\in P}{\max }⟨q,p⟩$相似度，对$\text{Top-}k$个文档进行重排
3. 备注的点：
   • ${\mathbf{F}}_{\text{doc}}/{\mathbf{F}}_{\text{que}}$是与数据分布无关，由此对不同分布的处理都有鲁棒性
   • $⟨{\mathbf{F}}_{\mathrm{que}}(Q),{\mathbf{F}}_{\text{doc}}(P_i)⟩$求解过程在高度优化的$\text{MIPS}$求解器中完成

$\text{2. }$固定维度嵌入($\text{FDEs}$)

$\text{2.1. FDE}$的生成过程

1️⃣文本嵌入：对查询文本和段落文本分别应用嵌入器(如$\text{ColBERTv2}$)，得到各自的多向量嵌入

1. 查询嵌入$Q$： { q 1 , q 2 , . . . , q m } \{q_1,q_2,...,q_m\} {q1​,q2​,...,qm​}，其中$q_i\text{⊆}{\mathbb{R}}^d$即为固定$d$维
2. 段落嵌入$P$： { p 1 , p 2 , . . . , p n } \{p_1,p_2,...,p_n\} {p1​,p2​,...,pn​}，其中$p_i\text{⊆}{\mathbb{R}}^d$即为固定$d$维

2️⃣向量分桶：用$\text{SimHash}$将原有空间分为$2^{k_{\text{sim}}}$个桶，每个桶用长为$k_{\text{sim}}$的定长二进制向量编码

1. 法向抽取：从高斯分布中抽取$k_{\text{sim}}\text{≥}1$个向量$g_1,\dots ,g_{k_{\text{sim}}}\text{∈}{\mathbb{R}}^d$，作为$k_{\text{sim}}$个超平面的法向量
2. 空间划分：$\phi (x)\text{=}\left(1\left(⟨g_1,x⟩\text{>}0\right),\dots ,1\left(⟨g_{k_{\text{sim}}},x⟩\text{>}0\right)\right)$
   • $1\left(⟨g_i,x⟩\text{>}0\right)$：当$⟨g_i,x⟩\text{>}0$成立(即$x$投影在超平面$g_i$的正侧)时，将该位设为$1$
3. 向量分桶：让所有的$m\text{+}n$个嵌入通过$\phi (\cdot )$得到长$k_{\text{sim}}$的二进制编码，相同编码者(即桶编码)放入同一桶

3️⃣向量生成：按照如下三种情况，为每个桶$k$都生成一个子向量${\vec{q}}_{(k)},{\vec{p}}_{(k)}\text{⊆}{\mathbb{R}}^d$

$\text{Case}$	桶$\mathbf{k}$的情况	桶$\mathbf{k}$子向量${\vec{\mathbf{q}}}_{(\mathbf{k})}$	桶$\mathbf{k}$子向量${\vec{\mathbf{p}}}_{(\mathbf{k})}$
$\text{Case-0}$	无 p i → { q 1 , q 2 , . . . ∣ } p_i\text{→}\{q_1,q_2,...\mid{}\} pi​→{q1​,q2​,...∣}	${\vec{q}}_{(k)}=\sum q_i$	${\vec{p}}_{(k)}=$与该桶海明距离最近的$p$
$\text{Case-1}$	单 p i → { q 1 , q 2 , . . . ∣ p } p_i\text{→}\{q_1,q_2,...\mid{}p\} pi​→{q1​,q2​,...∣p}	${\vec{q}}_{(k)}=\sum q_i$	${\vec{p}}_{(k)}=p$
$\text{Case-n}$	多 p i → { q 1 , q 2 , . . . ∣ p 1 , p 2 , . . . } p_i\text{→}\{q_1,q_2,...\mid{}p_1,p_2,...\} pi​→{q1​,q2​,...∣p1​,p2​,...}	${\vec{q}}_{(k)}=\sum q_i$	${\vec{p}}_{(k)}=\frac{1}{\#p}\sum p_j$($p$的质心)

4️⃣向量压缩：对每个${\vec{q}}_{(k)},{\vec{p}}_{(k)}\text{⊆}{\mathbb{R}}^d$应用随机线性投影$\psi \text{:}{\mathbb{R}}^d\text{→}{\mathbb{R}}^{d_{\text{proj}}}(d_{\text{proj}}\text{≤}d)$

1. 投影函数：$\mathbf{\psi }(x)\text{=}\left(\frac{1}{\sqrt{d_{\text{proj}}}}\right)\mathbf{S}x$，其中$\mathbf{S}\text{∈}{\mathbb{R}}^{d_{\text{proj}}\text{×}d}$为随机矩阵
   • 当$d_{\text{proj}}\text{=}d$时$\mathbf{S}$的每个元素$s_{ij}\text{=}1$，即$\mathbf{\psi }(x)\text{=}x$
   • 当$d_{\text{proj}}\text{<}d$时$\mathbf{S}$的每个元素$s_{ij}$满足离散均匀分布$\mathbb{P}r\left[s_{ij}\text{=}1\right]\text{=}\mathbb{P}r\left[s_{ij}\text{=}–1\right]\text{=}\frac{1}{2}$
2. 投影操作：$\{\begin{array}{l}{\vec{q}}_{(k),\psi }\text{⊆}{\mathbb{R}}^{d_{\text{proj}}}\stackrel{\psi \left({\vec{q}}_{(k)}\right)}{\leftarrow }{\vec{q}}_{(k)}\text{⊆}{\mathbb{R}}^d\\ \\ {\vec{p}}_{(k),\psi }\text{⊆}{\mathbb{R}}^{d_{\text{proj}}}\stackrel{\psi \left({\vec{p}}_{(k)}\right)}{\leftarrow }{\vec{p}}_{(k)}\text{⊆}{\mathbb{R}}^d\end{array}$
3. 合并操作：将每个桶的压缩向量依次从左到右合并$\text{→}\{\begin{array}{l}{\vec{q}}_{\psi }\text{=}\left({\vec{q}}_{(1),\psi },\dots ,{\vec{q}}_{(B),\psi }\right)\text{⊆}{\mathbb{R}}^{d_{\text{proj}}{2}^{k_{sim}}}\\ \\ {\vec{p}}_{\psi }\text{=}\left({\vec{p}}_{(1),\psi },\dots ,{\vec{p}}_{(B),\psi }\right)\text{⊆}{\mathbb{R}}^{d_{\text{proj}}{2}^{k_{sim}}}\end{array}$

5️⃣重复生成：重复2️⃣$\text{→}$4️⃣过程$R_{\text{reps}}$次，每次重复完成后生成${\vec{q}}_{i,\psi },{\vec{p}}_{i,\psi }$，拼接所有${\vec{q}}_{i,\psi },{\vec{p}}_{i,\psi }$

1. $Q$最终生成的单向量：${\mathbf{F}}_{\mathrm{que}}(Q)\text{=}\left({\vec{q}}_{1,\psi },\dots ,{\vec{q}}_{R_{\text{reps}},\psi }\right)\text{⊆}{\mathbb{R}}^{d_{\text{proj}}{2}^{k_{sim}}{R}_{\text{reps}}}$
2. $P$最终生成的单向量：${\mathbf{F}}_{\mathrm{doc}}(P)\text{=}\left({\vec{p}}_{1,\psi },\dots ,{\vec{p}}_{R_{\text{reps}},\psi }\right)\text{⊆}{\mathbb{R}}^{d_{\text{proj}}{2}^{k_{sim}}{R}_{\text{reps}}}$

6️⃣相似度：和但向量模型一样，就是二者的内积$⟨{\mathbf{F}}_{\mathrm{que}}(Q),{\mathbf{F}}_{\mathrm{doc}}(P)⟩$

$\text{2.Muvera}$的理论保证

0️⃣一些前提

1. 归一化的$\text{Chamfer}$相似度：$\text{NChamfer}(Q,P)\text{=}\frac{1}{|Q|}\text{Chamfer}(Q,P)\text{∈}[-1,1]$，即$\text{MaxSim}$平均值-
2. 默认所有的嵌入都归一化：$\{\begin{array}{l}\Vert q{\Vert }_2\text{=}\sqrt{q_1^2\text{+}{q}_2^2\text{+}\cdots \text{+}{q}_n^2}\text{=}1\\ \\ \Vert p{\Vert }_2\text{=}\sqrt{p_1^2\text{+}{p}_2^2\text{+}\cdots \text{+}{p}_n^2}\text{=}1\end{array}$

1️⃣定理$\text{2-1}$：$\text{FDE}$对$\text{Chamfer}$相似度的近似程度，可以达到$\epsilon \text{-}$加相似性

1. 给定条件：对于$\forall \epsilon ,\delta \text{>}0$，设定$m\text{=}|Q|\text{+}|P|$
2. 设定参数：$\{\begin{array}{l}{k}_{\text{sim}}\text{=}O\left(\frac{\log \left(m{\delta }^{-1}\right)}{\epsilon }\right)\\ \\ d_{\text{proj}}\text{=}O\left(\frac{1}{{\epsilon }^2}\log \left(\frac{m}{\epsilon \delta }\right)\right)\\ \\ R_{\text{reps}}\text{=}1\end{array}\Rightarrow d_{\text{FDE}}\text{=}{\left(\frac{m}{\delta }\right)}^{O\left(\frac{1}{\epsilon }\right)}$
3. 结论：$\frac{1}{|Q|}⟨{\mathbf{F}}_{\text{que}}(Q),{\mathbf{F}}_{\text{doc}}(P)⟩\text{∈}[\text{NChamfer}(Q,P)\text{–}\epsilon ,\text{NChamfer}(Q,P)\text{+}\epsilon ]$以$P\text{≥}1–\delta$概率成立

2️⃣定理$\text{2-2}$：将原有的$P$便变成$P_i$，即一个查询对多个段落

1. 给定条件：对于$\forall \epsilon \text{>}0$，设定$m\text{=}|Q|\text{+}|P_i{|}_{\text{max}}$
2. 设定参数：$\{\begin{array}{l}{k}_{\text{sim}}\text{=}O\left(\frac{\log m}{\epsilon }\right)\\ \\ d_{\text{proj}}\text{=}O\left(\frac{1}{{\epsilon }^2}\log (\frac{m}{\epsilon })\right)\\ \\ R_{\text{reps}}\text{=}O\left(\frac{1}{{\epsilon }^2}\log n\right)\end{array}\Rightarrow d_{\text{FDE}}\text{=}{m}^{O\left(\frac{1}{\epsilon }\right)}\text{×}\log n$
3. 结论$1$：假设$P_i$是用$\text{Muvera}$方法找到的最相似文档，$P_j$是真实的最相似文档
   • $\text{NChamfer}\left(Q,P_i\right)$和$\text{NChamfer}\left(Q,P_j\right)$互相的差距不会大于$\epsilon$
   • 该结论以$1\text{–}\frac{1}{\text{poly}(n)}$的概率成立
4. 结论$2$：从 { P 1 , … , P n } \{P_{1},\ldots,P_{n}\} {P1​,…,Pn​}中找出最$Q$的最相似文档耗时 O ( ∣ Q ∣ max ⁡ { d , n } 1 ε 4 log ⁡ ( m ε ) log ⁡ n ) \displaystyle{}O\left(|Q|\max\{d,n\}\frac{1}{\varepsilon^{4}}\log{}\left(\frac{m}{\varepsilon}\right)\log{}n\right) O(∣Q∣max{d,n}ε41​log(εm​)logn)

$\text{3. }$实验及结果

$\text{3.1. }$离线检索的评估

1️⃣离线的实现

1. 向量生成：用$\text{ColBERTv2}$为每个$\text{Token}$生成$\text{128}$维的向量，同时强制查询向量数固定$m\text{=}32$
2. 检索设置：让$\text{Muvera}$对段落进行排序(不进行任何重排)，并以真实的$\text{Chamfer}$相似度为基准评估

2️⃣$\text{Muvera}$实验结果

1. 维度$/$参数对$\text{Muvera}$性能的影响
   
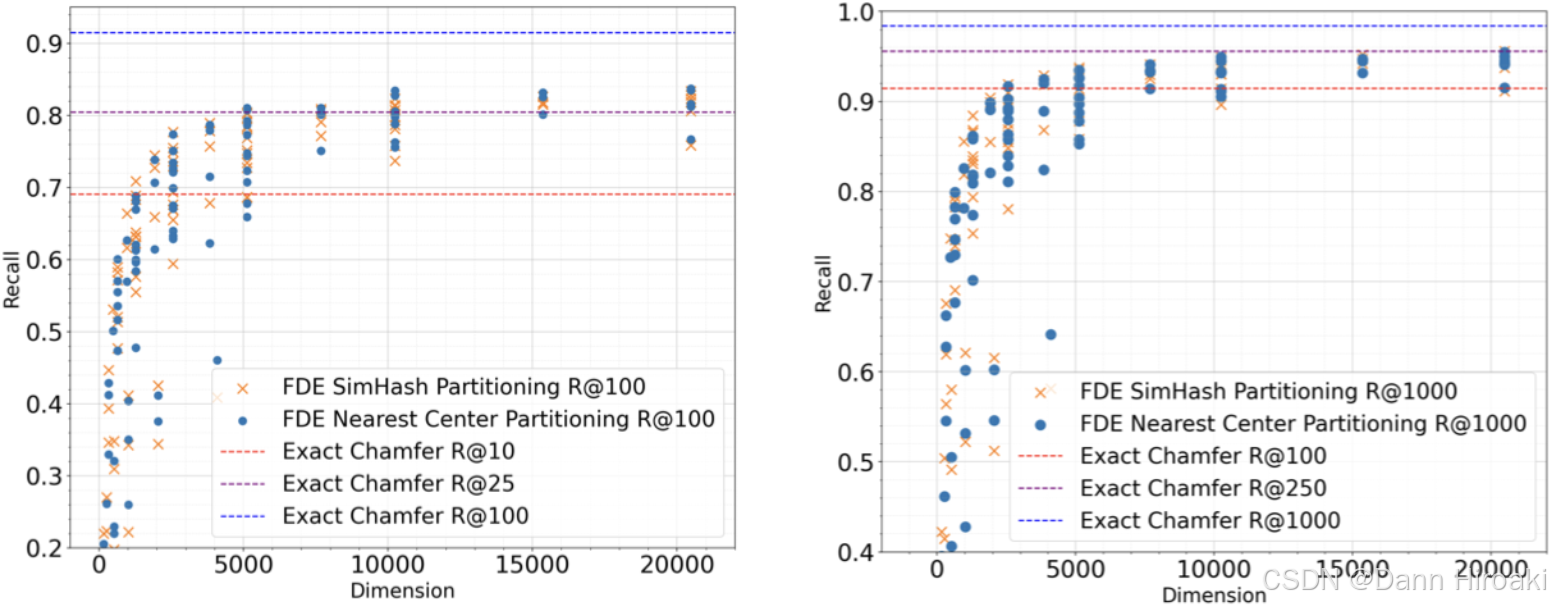
   • 维度变化时：随着总维度$d_{\text{FDE}}\text{=}{d}_{\text{proj}}{2}^{k_{sim}}{R}_{\text{reps}}$的提升$\text{Muvera}$的检索质量提高
   • 维度限定时：参数设置 ( R reps , k sim , d proj ) ∈ { ( 20 , 3 , 8 ) , ( 20 , 4 , 8 ) ( 20 , 5 , 8 ) , ( 20 , 5 , 16 ) } \left({{R}_{\text{reps}},{k}_{\text{sim}},{d}_{\text{proj}}}\right)\text{∈}\{\left({{20},3,8}\right),\left({{20},4,8}\right)\left({{20},5,8}\right),\left({{20},5,{16}}\right)\} (Rreps​,ksim​,dproj​)∈{(20,3,8),(20,4,8)(20,5,8),(20,5,16)}在各自总维度上$\text{Pareto}$最优
2. 与$\text{Chamfer}$距离：以暴力算出的$\text{Chamfer}$结果为基准(而非真实标注数据)的结果
   
3. 不同实现的对比：将$\text{SimHash}$分桶过程用$k\text{-Means}$分簇代替后，相同维度$\text{Muvera}$取得的性能下降

3️⃣与启发式单向量

1. 启发式单向量：给定一个查询 Q = { q 1 , q 2 , . . . , q m } Q\text{=}\{q_1,q_2,...,q_m\} Q={q1​,q2​,...,qm​}和一个包含$N$个段落的段落集$\mathcal{P}\text{=}\left\{P^{(1)},P^{(2)},\dots ,P^{(N)}\right\}$
   • 检索：让每个$q_i\text{∈}Q$在所有段落子向量集$P^{(1)}\text{∪}{P}^{(2)}\text{∪}\dots \text{∪}{P}^{(N)}$中执行$\text{MIPS}$(最大内积搜索)，得到$\text{Top-}K$的段落子向量
   • 回溯：合并$n$个$q_i$的$\text{Top-}K$共$n\text{×}K$个段落向量，回溯每个向量到其所属段落得候选集${\mathcal{P}}^{\prime }\text{=}\left\{P^{(1)},P^{(2)},\dots ,P^{(M)}\right\}$
   • 重排：基于精确的$\text{Chamfer}\left(Q,P^{(i)}\right)$距离对候选集${\mathcal{P}}^{\prime }$进行排序，得到最终最相似段落
2. 成本对比：要让 Q = { q 1 , q 2 , . . . , q m } Q\text{=}\{q_1,q_2,...,q_m\} Q={q1​,q2​,...,qm​}对$\mathcal{P}\text{=}\left\{P^{(1)},P^{(2)},\dots ,P^{(N)}\right\}$进行查询，假设$\mathcal{P}$中向量平均长度位$n_{\text{avg}}$
   • $\text{Muvera}$的成本：让$Q$扫描$N$个但向量即可，每个向量为$d_{\text{FDE}}$维，故一共需要扫描$N\text{×}{d}_{\text{FDE}}$个浮点数(远小于后者)
   • 启发式单向量成本：每个$q_i$都要扫描$n_{\text{avg}}$个向量(共$m\text{×}{n}_{\text{avg}}$个向量)，每次扫描涉及$d$个浮点数故一共$d\text{×}m\text{×}{n}_{\text{avg}}$个
3. 实验结果：对比$\text{Muvera}$不同维度(各自$\text{Pareto}$最优)，以及启发式单向量$\text{(SV)}$对候选段落去重$/$不去重版本
   

$\text{3.2. }$在线端到端的结果

1️⃣端到端的实现

1. 整体流程：粗筛$\text{+}$重排
   • 粗筛：将多向量用$\text{Muvera}$转为单向两，用$\text{DiskANN}$对单向两进行搜索，得到候选段落
   • 重排：基于$\text{Chamfer}$相似度对候选段落进行重排
2. 球分割：对 Q = { q 1 , q 2 , . . . , q m } Q\text{=}\{q_1,q_2,...,q_m\} Q={q1​,q2​,...,qm​}进行压缩，使得$Q$中向量数目远小于$m$
   • 对于集合 Q = { q 1 , q 2 , . . . , q m } Q\text{=}\{q_1,q_2,...,q_m\} Q={q1​,q2​,...,qm​}，每次从集合$Q$中随机选取一种子点$q_i$
   • 计算$q_i$与$Q$中剩余点的相似度，相似度大于阈值$\tau$者从$Q$中取出分到$q_i$的簇
   • 以此类推贪心地执行下去，不断从剩余集合中取出种子点，再用种子点取出向量构成簇，构成若干簇
   • 得到簇质心集 Q C = { q c 1 , q c 2 , . . . , q c k } Q_C\text{=}\{q_{c_1},q_{c_2},...,q_{c_k}\} QC​={qc1​​,qc2​​,...,qck​​}，其中$k\text{＜}m$故可将$Q_C$看作$Q$的一个近似量化
3. $\text{PQ}$量化：对$\text{Muvera}$向量${\mathbf{F}}_{\mathrm{doc}}(P)$进行压缩，使得其维度远小于$d_{\text{FDE}}$，用$\text{PQ-C-G}$表示每$G$维用$C$个质心量化

2️⃣实验结果

1. $\text{QPS}$与召回：$\text{PQ-256-8}$方案的端到端实现最具性能，并且$\text{Muvera}$对数据的依赖较小
   
2. 与$\text{PLAID}$的对比：总的来说就是与$\text{PLAID}$检索质量相当(甚至更优)，但是延迟大大降低