状态压缩DP(蒙德里安的梦想、最短Hamilton路径)

蒙德里安的梦想

题目背景

求把 N×M 的棋盘分割成若干个 1×2 的长方形，有多少种方案。

例如当 N=2，M=4 时，共有 5 种方案。当 N=2，M=3 时，共有 3 种方案。

算法描述

首先，1×2的长方形只可以横着放，或者竖着放。一旦我们把所有横着放的长方形确定且合法，那么竖着放的长方形只有唯一的放法。因而我们就将题目转化为了有多少种合法的，横着的长方形摆法。

举个例子：我们关注橙色区域的2×4的棋盘：

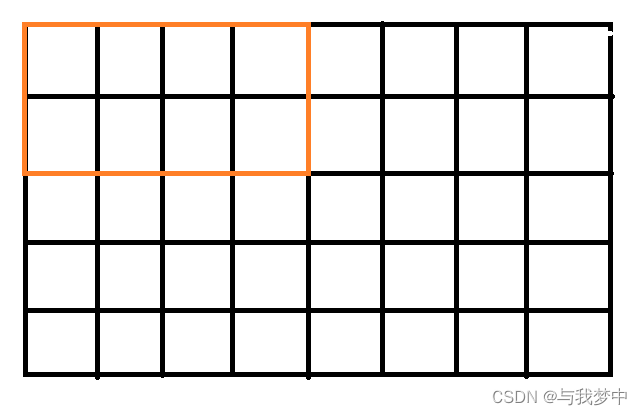
我们长方形的摆放方法有：

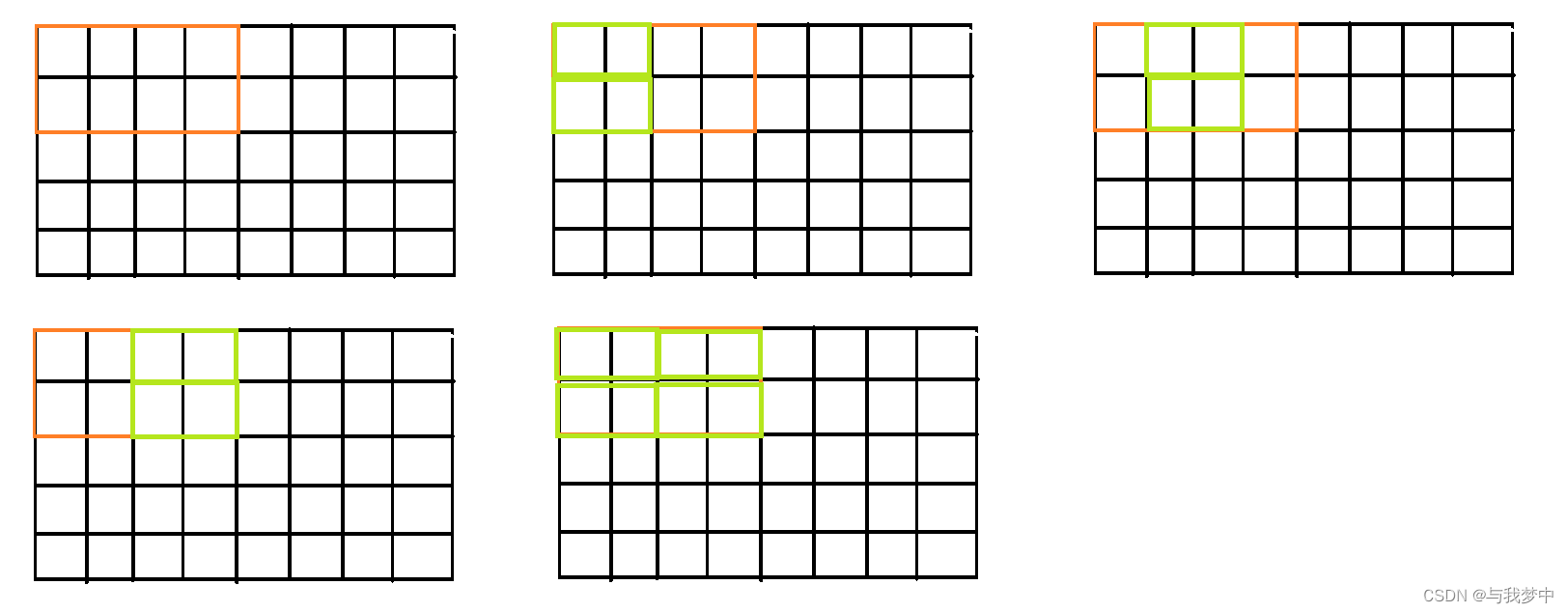
棋盘剩下的位置，竖着的长方形摆放的方法唯一。而这样的摆放方法就是不可行的

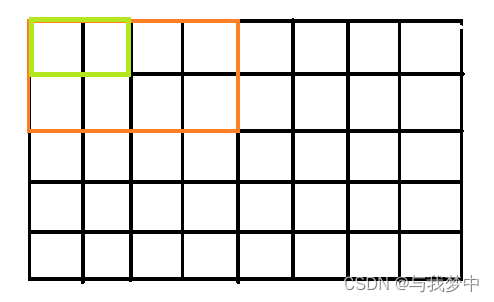
因为第2行，第1列和第2列的格子没有办法填满。

状态表示

我们现在考虑第1列横着的长方形可以有多少种放法：事实上，每一行我都可以选择放置或不放置长方形，那我们如何表示每一种放法，棋盘对应的状态？

这也就是状态压缩DP问题比较关键的地方。对于某一列，我们现在有5行，若在这一行我们放置长方形，则置为1；若这一行我们不放置长方形，则置为0，所以每一种方法都可以对应一个5位的二进制数，唯一地对应0-31种地某一个数。例如下图第1列对应的二进制数为21(10101).

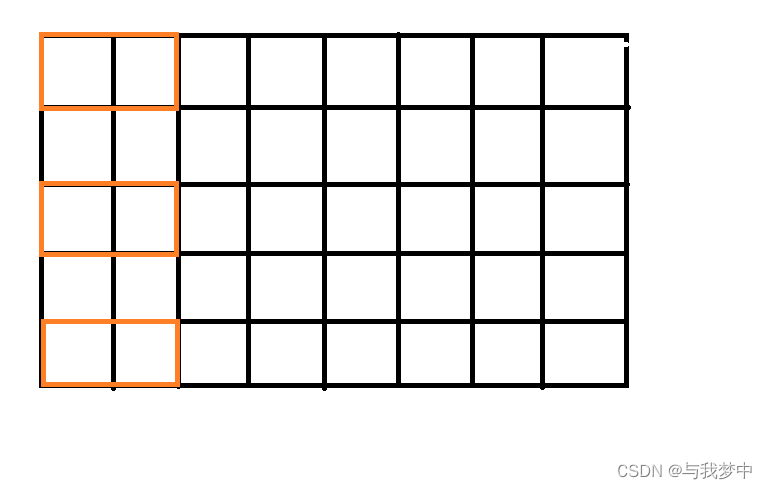
现在我们定义f[i][j]=k为第i列状态为j时有共有k种摆放的方法。

状态转移

现在我们考虑的问题是，如何求f[i][j]的值？我们以i=3，j=10(01100)为例：

首先，f[3][10]在第3列摆放的长方形示意图为：

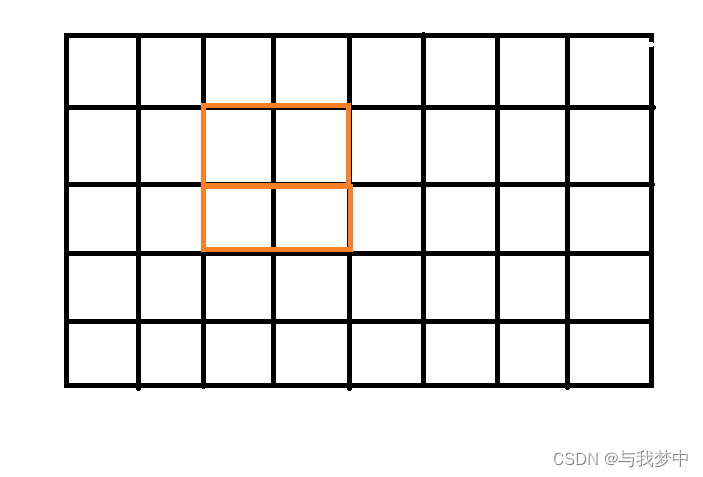
那我们发现，对于i-1列，摆放长方形的情况可以为：

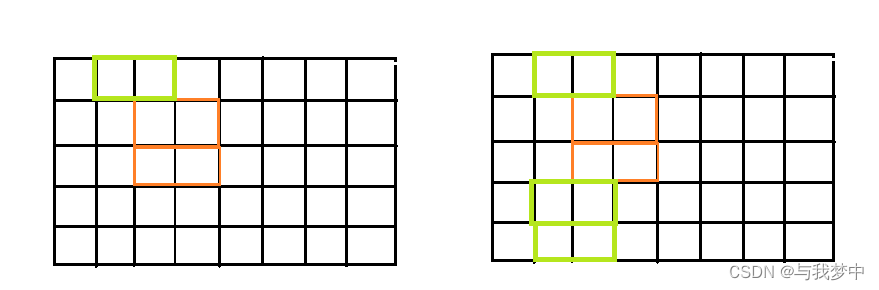
2幅图对应的i-1列状态分别为f[2][16],f[2][19],这样，f[3][10]=f[2][16]+f[2][19].

以下情况是不可以的：

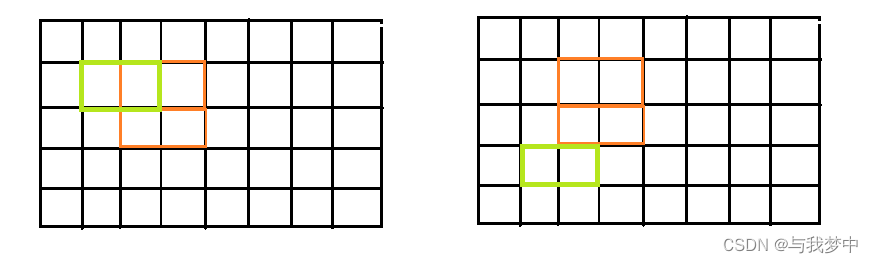
对于左边的情况，很明显，由于第2行放置长方形凸出来了一块，第3列就不能放置了；对于右边的情况，这是因为，第一行和第五行没有放置长方形，但是同时也放不下竖着的长方形了。

所以可以总结，当我们要求f[i][j]对应的状态数时，f[i-1][0:31]都对应着一个数，表示i-1列状态为j时总共有多少种放法。那如果f[i][j*]和f[i-1][j]不冲突的话，前i-1列的每一种放法，再在第i列按照状态j=j*放置，都是合法的，我再把第i列剩下的格子用竖着的长方形填满，一定可以保证5×i的棋盘可以填满(不考虑第i+1列突出去的块)。所以状态状态方程为：f[i][j]=f[i-1][k](0≤k≤31 且f[i][j]和f[i-1][k]不冲突)。

而冲突的情况也很显然，分别对应上图的两种情况：
①我们从二进制的角度看，即同一位上都是1，这样k&j!=0。
②我们可以发现，当连续出现2i+1行空格是会冲突的，因为竖的长方形没有办法填满，此时第i行为空格即i-1列和第i列都没有放置长方形，对于的二进制位都是0，所以k|j会有奇数个位为0.

递归结束的条件

对于求f[1][j]时，会要用到f[0][k]，但事实上，我们不允许第0列有插入的长方形，因为这样第1列就会有1*1的长方形。因而f[0][1:31]=0.因而第0列只能一个都不放,对应一种方案，f[0][0]=1。

最后第m列我们是不允许插入长方形的，因为这样会在m=1列突出一块，同样的，在第m列会有1*1的长方形块，所以第m列我们只可以看j=0时有多少种摆放的放法。由前面的分析我们知道，可以保证m列的棋盘摆满。。下图即为一种第m列不放置横的长方形时，i-1列不冲突的一种情况：

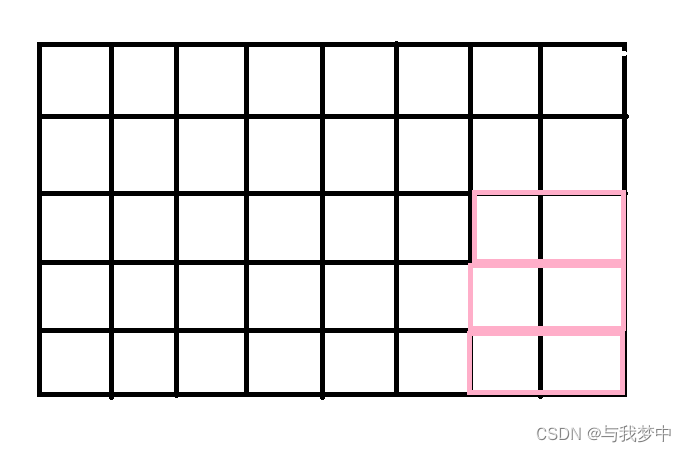
代码实现

在给出状态转移方程的基础上，状态计算的代码就很简单了：

for(int i=1;i<=m;i++){
                for(int j=0;j<=Max_j;j++){
                    for(int k=0;k<=Max_j;k++){
                        if(!(k&j) && st[k|j]) f[i][j]+=f[i-1][k];
                    }
                }
            }

但是我们关键是 st[]数组，即我们将k或上j，对应的到底是不是一个合法的操作？

在开始我们会想，若1≤n,m≤11，那么状态j的范围为：[0,2¹¹-1]，自然，我们将j|k也会∈[0,2¹¹-1]，所以我们是否可以遍历一边[0,2¹¹-1]中的每一个数i，看i是否存在连续奇数个的0？

然而，这种做法是不可以的。

我们举个例子：假设我们现在的矩阵是2*2，我们考虑j|k=1，这样我们得到的结果是有0个0，不存在连续的奇数个的0，所以st[1]=true.

但事实上，若i-1列状态j=1，即表示在第二列插入了一个长方形，那这样第一列不就没有办法用竖着的长方形填满了吗？此时应该为：st[1]=false
但是若矩阵为2*3，st[1]=true，结果又是对的，那为什么会这样呢？

这是因为，当矩阵有x行的时候，我们应该用x位去表示每一个二进制数。对于上述的例子，n=2时，1应该写成01，这时候出现了一个0，所以str[1]=false;而n=3时，1应该写成001，这时候出现的是连续的两个0，所以str[1]=true,这样就没有问题了。

所以下面求解的放法是错误的：

while(i>0) {
	if(!i&1){
		cnt++;
		i>>=2;
	}
} 

要修改也很容易想到，n位时，我们要把n位都算上，尽管可能前几位都是0：

while(n--) {
	if(!i&1){
		cnt++;
		i>>=2;
	}
} 

但是我们仍需注意一个问题，假设现在j|k=0001，n=4.执行4次，此时在遍历到最前面的0时，cnt=3，但是程序已经退出while循环了，flag仍然没有被置为1（我们用flag记录是否会有冲突），所以最后我们在给st[i]置为true时，判断条件应为：if(cnt%2==0 && !flag)，这样就没有问题了。

完整代码：

#include<iostream>
#include<math.h>
#include<cstring>
using namespace std;
const int N=15;
const int M=3000;
int n,m;//n×m
bool st[M];//对应的或的结果合不合法(有没有连续的奇数个的0)
long long f[N][M];
int main(){
    while(1){
        memset(st,0,sizeof(st));//***************
        memset(f,0,sizeof(f));//要先清空
        f[0][0]=1;
        cin>>n>>m;
        if(n==0 && m==0) break;
        else{
            int Max_j=pow(2,n)-1;
            int i=0;
            while(i<=Max_j){
                int cnt=0,tmp=i,flag=0,num=n;
                while(num--){
                    if(!(tmp&1)) cnt++;//如果最后一位是0，那么cnt++
                    else{//如果此时为1
                        if(cnt%2){
                            st[i]=false;//奇数个的话，那就是false，会冲突
                            flag=1;
                            break;
                        }
                        cnt=0;
                    }
                    tmp=tmp>>1;//右移一位
                }
                if(!flag && cnt%2==0) st[i]=true;
                i++;
            }
            for(int i=1;i<=m;i++){
                for(int j=0;j<=Max_j;j++){
                    for(int k=0;k<=Max_j;k++){
                        if(!(k&j) && st[k|j]) f[i][j]+=f[i-1][k];
                    }
                }
            }
            printf("%lld\n",f[m][0]);
        }
    }
}

最短Hamilton路径

题目背景

给定一张 n 个点的带权无向图，点从 0∼n−1 标号，求起点 0 到终点 n−1 的最短 Hamilton 路径。

Hamilton 路径的定义是从 0 到 n−1 不重不漏地经过每个点恰好一次。

算法描述

状态表示

根据状态压缩的思想，对于n个结点的图，我们可以想到(反正我想不到)用n位二进制的数来表示当前图的状态：1表示已经讲过该结点，0表示还没有经过该结点。

举个简单的例子，对于n=5的图，17=10001B,即17表示已经经过了第0个和第4个结点(高位是下标更大的结点)。

但是这显然不够呀，就好比上述的例子，遍历顺序为0→4以及4→0对应的都是17，那位了表示当前我们遍历到的结点，我们用f[i][j]表示从结点0到结点j，状态为i的所有路径的集合。i就体现的是，从结点0到结点j，中间经过了哪些结点。

属性

很显然，f[i][j]=k表示从结点0到结点j，状态为i的路径长度最小值为k。

状态计算

那我们如何计算状态转移方程？我们把集合按照倒数第二个结点进行分类。我们仍然令n=6，此时f[55][1] 表示从结点0到结点1，状态为55的路径的最小值，状态表示为110111.那么现在可以有以下几种情况：
①倒数第二个结点为2，这样遍历结点的顺序为：0-(4,5)-2-1；
②倒数第二个结点为4，这样遍历结点的顺序为：0-(2,5)-4-1；
③倒数第三个结点为5，这样遍历结点的顺序为：0-(2,4)-5-1；
其中()的意思是括号内的结点遍历顺序随意。

对于情况①，根据定义，路径长度的最小值会等于0-(4,5)-2路径长度的最小值，也就是0经过4，5结点到达2的最小路径长度加上w[1][2].对应的状态为110110B=54，所以f[55][1]=f[54][2]+w[1][2];

对于情况②，路径长度的最小值会等于0-(2,5)-4路径长度的最小值加上w[4][1]，对应的状态也为54，所以f[55][1]=f[54][4]+w[1][4].

对应情况③，类似地，f[55][1]=f[54][5]+w[1][5].

因而我们可以看到，我们在选定了倒数第二个结点k之后，我们只需要将当前结点j对应地二进制位减去即可。

总结：对于求f[i][j]，现在从结点0到结点j遍历过的结点状态为i。它的前一个结点为k时，从0到k的路径经过的结点状态为i-1<<j,这是因为下一步结点k就要去结点j，结点0到结点k经过的结点只和i相差一个2^j,所以我们将1左移j位，这样，f[i][j]=f[i-1<<j][k]+w[j][k]。

注意事项

①我们可能会习惯的想，遍历顺序为:

for(int j=0;j<n;j++)
	for(int i=0;i<1<<n;i++)

注：因为对于n个结点的图，状态表示为n位，这样i的范围为[0:2ⁿ-1],刚好1<<n是2ⁿ。

上述按结点的顺序来遍历，但事实上，我们想象以下，我们此时j=1，而把i全部遍历了一遍，就拿状态计算中的例子来看：f[55][1]=f[54][2]+w[1][2]，可是现在我j还没到2呢，f[54][2]还没求出来…

所以不能按照先遍历点，再遍历所有状态的顺序。

那如果我们换一下：

for(int i=0;i<1<<n;i++)
	for(int j=0;j<n;j++)

这样对于每一个状态，我们都把它到的结点遍历了一遍。再拿这个例子来看：110111，我们从j=0→5，也就是说这个序列代表着4种情况(最后到达的是1，2，4，5结点)，这个时候我们再去计算状态转移时，f[55][1]=f[54][4]+w[1][4]，那由于我会把当前结点j从1置为0，所以可以看到f[i][j]=f[i-1<<j][k]+w[j][k]，(i-1<<j)<i，所以f[54][4]我是一定计算好了的。因而我们外层循环是状态，内层循环是这个状态中最后到达的结点。

当然，对于110111这个结点，最后一个结点不可能是3，所以自然我们也不会更新f[55][3]，我们也用不到f[55][3]，这是因为我们选择倒数第二个结点，肯定也是会选对应位为1的结点。所以我们增加if(i>>j&1)的判断条件，只有该位为1才更新。

②初始条件以及求解最终答案

边界条件一直让我很头疼…假设n=6，这样初始状态为000000，表示还没有开始走，但是由于规定了起点是第0个结点，所以初始状态为000001，而更新f[1][0]的时候，用不了f[55][1]=f[54][4]+w[1][4]公式，因为我前边压根儿没有结点啊，我是第一个结点，所以这就是我们的临界的条件，f[1][0]表示从结点0到结点0的路径长度，当然为0了，f[1][0]=0。

但是我们会想，比如状态i=2的时候，此时状态用二进制表示为000010，这个第1个结点前面不是也没有任何结点吗？所以我们进行了初始化:memset(f,0x3f,sizeof(f));所以，即使我们只把第j位的1置为了0，没有把第0位置为0，我们把0作为倒数第二个结点，f[i-1<<j][k]这一项一定是无穷大的，这是因为你不断往前找倒数第二个结点，最后找到第一个结点时，它的f的值一定是正无穷。

举个例子：就比如1100001，你非要让第0位是0，那就会找f[11000B][0],下面就会找f[10000B][3],但我们说过了，由于第5个结点前面没有结点了，最后f[10000B][3]=∞，所以一定是比不过别人滴。

最终答案对应什么呢？要求0到n遍历所有点的路径的最下值，首先j=n-1，由于遍历了所有点，这样所有位为1，所以对应f[(1<<n)-1][n-1].

具体代码为：

#include<iostream>
#include<cstring>
#include<math.h>
#include<algorithm>
using namespace std;
const int N=21;
const int M=1<<N;
int w[N][N];
int f[M][N];
int main(){
    int n;
    cin>>n;
    for(int i=0;i<=n-1;i++){
        for(int j=0;j<=n-1;j++){
            cin>>w[i][j];
        }
    }
    //initialization
    memset(f,0x3f,sizeof(f));
    f[1][0]=0;//从结点0走到0，状态表示是1，走过用1表示
    for(int i=0;i<1<<n;i++){
        for(int j=1;j<n;j++){//对于n位，状态i的范围是[0:(2^n)-1]，其实可以用i<<n=2^n
            //既然是0到结点j，那么结点j对应的位一定要是1，如果不是1我们就不更新了
            if(i>>j&1){
                for(int k=0;k<n;k++){//前一个结点可以是除自己以外的所有结点，但是你那个结点得是1呀
                    if((i-(1<<j)>>k)&1){//第k位是1的情况下，i-(1<<j)的目的是不会说结点j的上一个结点是j
                        f[i][j]=min(f[i][j],f[i-(1<<j)][k]+w[k][j]);
                    }
                }
            }
        }
    }
    cout<<f[(1<<n)-1][n-1];
}

感谢AcWing平台