用C++解决八皇后问题（超简单一学就废+极简版代码30行）

本文链接：https://blog.csdn.net/qq_64934572/article/details/129372328

文章介绍了八皇后问题的背景，这是一个经典的编程挑战，目标是在国际象棋棋盘上放置八个皇后，使得任何两个皇后都不在同一行、同一列或同一对角线上。作者提供了极简版和完整版的C++代码实现，使用了回溯算法来解决这一问题，完整版代码包括了详细的解释和条件判断。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

什么是八皇后

八皇后？八皇后！好想法！（八个皇后，那我要是国王...）但只可惜此皇后，非彼皇后，此皇后乃是国际象棋的棋子，咱先不说问题，先看看这个问题有多吊（怕你们看半道走人了，不玩了）。八皇后问题如果暴力硬解有 $8^{8}$ 种（注意，这还是已经用掉了部分条件的结果），高斯说有72种，但实际上有92种（感觉高斯不如我+计算机（高斯看了想打人））。

那么下面我们来正式介绍八皇后问题：众所周知（做题得知）国际象棋棋盘为8 $\times$ 8(围棋多少？不知道吧？自己查！),现在我们要往上面放八个皇后，我们假设八个皇后隶属于八大门派，她们各自为敌，现在我们要让她们全部放在棋盘上但相安无事。所以，我们要保证任意两个皇后不在棋盘的水平或者竖直的一条线上，也不能在斜线上。大概就是这样

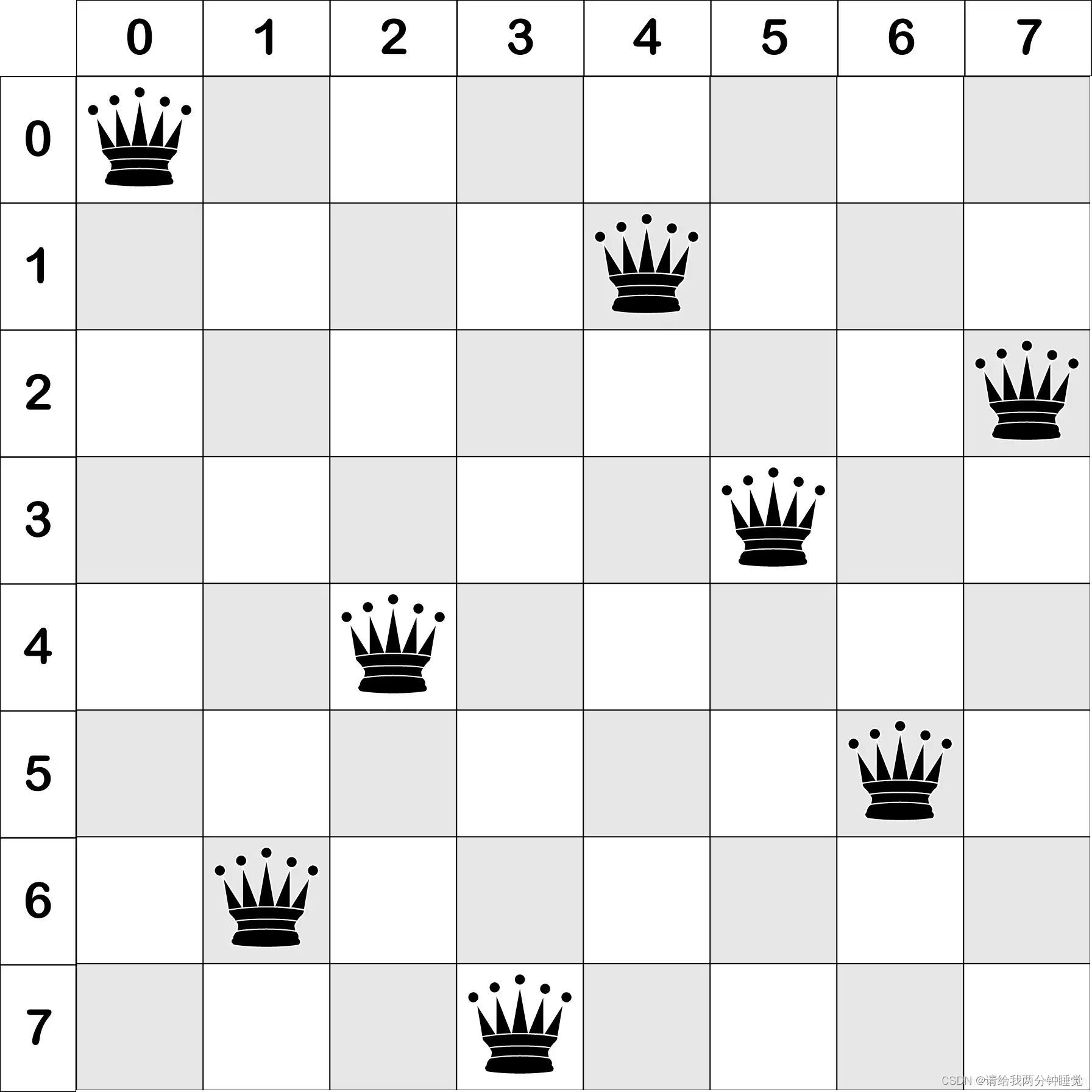
OK下面我们来完成高斯未竟的答案吧。

代码展示（极简版）

为了展示本代码的先进性，鄙人用尽了一切手段使其代码行控制在30行以内（是故意的），大家图一乐，建议看后面的完整代码，里面有解释的。

#include <iostream>
#include <vector>
using namespace std;
int available(vector<int>,int);
int play(vector<int>&);
int main()
{
    vector<int> queen;//create a stack
    cout << play(queen) << endl;//enter recursion
}
int play(vector<int> &v)
{
    int sum = 0;
    for (int i = 0; i < 8; i++) {   //per piece
        if (available(v, i) && v.size() < 7) {
            v.push_back(i);
            sum += play(v);
            v.pop_back();
        }
        if (available(v, i) && v.size() == 7) sum += 1;  
    }
    return sum;
}
int available(vector<int> v,int k)//if position k is available for chess
{
    int pos = v.size();
    for (int i = 0; i < v.size(); i++)
        if (v[i] == k || (v[i] + i) == (k + pos) || (i - v[i]) == (pos - k)) return 0;      
    return 1;
}

完整版代码+解释

整体思路

八皇后问题是一个经典回溯算法，下面是具体想法：咱们一行一行下（一行肯定只有一个吧），先下一个棋子，再下满足条件的下一个，直到下满8个（8行下满）或已经没有满足条件的可下了，那么我们就开始回溯到上一层，继续下棋（下之前没下过的地方），回溯的方法就是用栈来实现，这里用的vector（这里和栈是一样的作用）。

代码+解释

main就不说了，我只能说懂得都懂。

先说说这里vector的思路，这里vector充当栈，为了是这个栈既装横坐标也装纵坐标，我们让vector的下标装横坐标(即是 横坐标==i)，vector里面的内容装纵坐标(即是 纵坐标==vector[i])。那么我们对栈里面装东西的时候自然也就实现了行比对，确保每一行没有重复的了

再说play函数，这个函数即为解决思路的大致实现，首先我们要计算数量所以初始化了一个sum来统计数量，然后设置了一个for循环，意在对每个点都进行循环8次的工作以此来确保每个点都尝试（你可能会问诶这样这样时间复杂度不就为O（ $n^{n}$ ）了吗，但实际上我们加了判定，在很早的阶段就可以避免很多情况的展开，运行时可以在瞬间完成计算）。OK，下满两个if判断是否当前位置可以下棋，如果没有下满七个，那么push进去，将栈传入下一个递归，有push就有pop呀，然后pop出来找下一个点，看能push进去不；如果已经下了7个了，那么直接sum++。

int play(vector<int> &v)
{
    int sum = 0;

    for (int i = 0; i < 8; i++) {   //每个下一步棋就遍历8次，确保每个位置都要试一下
        if (available(v, i) && v.size() < 7) {//满足条件（两两不在任意一条线上）的非最后一个棋子
            v.push_back(i);
            sum += play(v);
            v.pop_back();
        }
        if (available(v, i) && v.size() == 7) {//满足条件的最后一个棋子
            sum += 1;
            v.push_back(i);//弄进栈里边给兄弟们展示一下哪些图满足要求
            myshow(v);//展示函数
            v.pop_back();//弄进去之后还要弄出来
        }
    }
    return sum;
}

然后是available，一个看似简单实际也不难的条件判断，由于之前是一行一行的找，所以不必判断是否在一行，那么我们先判断是否是一列，之前说过列的信息存在vector[i]里，所以只需要比对要插入的位置是否与vector[i]相等即可这就是第一个条件v[i]==k；然后接着我们考虑斜线假设从落子坐标为（4，5）的点开始开始吧

（2，3）           （2，7）

                （3，4）（3，6）

                  （4，5）

可以看出右上到左下他们的和相等即(v[i] + i) == (k + pos)；做上到右下的斜线满足他们的差相等即(i - v[i]) == (pos - k)。

int available(vector<int> v,int k)//if position k is available for chess
{
    int pos = v.size();//已插入栈的位置
    for (int i = 0; i < v.size(); i++)//对前面每个点检查是否在一条竖线或者一条斜线上
        if (v[i] == k || (v[i] + i) == (k + pos) || (i - v[i]) == (pos - k))
            return 0;//不满足直接结束函数，返回

    return 1;
}

为了方便展示和检查我加了显示函数显示92张形如

的图并统计数字。（是不是比别人的代码良心）

看到这里直接完整版放送

完整版代码

#include <iostream>
#include <vector>
using namespace std;
int available(vector<int>,int);
int play(vector<int>&);
void myshow(vector<int>);//show the map
int main()
{
    vector<int> queen;//create a stack
    cout << play(queen) << endl;;//enter recursion
    system("pause");
}
int play(vector<int> &v)
{
    int sum = 0;

    for (int i = 0; i < 8; i++) {   //per piece
        if (available(v, i) && v.size() < 7) {
            v.push_back(i);
            sum += play(v);
            v.pop_back();
        }
        if (available(v, i) && v.size() == 7) {
            sum += 1;
            v.push_back(i);
            myshow(v);
            v.pop_back();
        }
    }
    return sum;
}
int available(vector<int> v,int k)//if position k is available for chess
{
    int pos = v.size(); 
    for (int i = 0; i < v.size(); i++)
        if (v[i] == k || (v[i] + i) == (k + pos) || (i - v[i]) == (pos - k))
            return 0;

    return 1;
}
void myshow(vector<int> v)
{
    for (int i = 0; i < 8; i++) {
        for (int j = 0; j < 8; j++) {
            if (v[i] == j)
                cout << 'o';
            else
                cout << 'x';
        }
        cout << endl;
    }
    cout << endl;
}