文章目录
- 质数
- 试除法判定质数
- 试除法分解质因数
- 朴素筛法求质数
- 埃氏筛法求质数
- 线性筛法求质数
- 欧拉筛法求质数
- 约数
- 试除法求所有约数
- 试除法求所有约数之和
- 约数个数和约数之和
- 欧几里得算法
- 欧拉函数
- 求欧拉函数
- 筛法求欧拉函数
- 快速幂
- 求快速幂
- 快速幂求逆元
- 扩展欧几里得算法
- 中国剩余定理
- 高斯消元
- 组合数
- 递推法求组合数
- 预处理逆元求组合数
- Lucas定理求组合数
- 分解质因数法求组合数
- 卡特兰数
- 博弈论
一、质数
1.试除法判定质数--O(sqrt(N))
原理:把从[2,n-1]中的每一个自然数作为除数来除n,如果n不能被其中的任意一个数整除,那么n就是素数。
优化:由于一个数的约数都是成对出现的。所以只需要枚举[2,sqrt(n)];
bool is_prime(int x)
{
if (x < 2) return false;
for (int i = 2; i <= x / i; i ++ )
if (x % i == 0)
return false;
return true;
}2.试除法分解质因数--O(logN)~O(sqrt(N))
原理:从[2,sqrt(n)]中枚举所有的质数,如果找到某一个素数i,则需要将n连续除以i得到m个i,然后将n中去除m个i的数,继续操作,如果最后一个数大于1,则得到最后一个质因子。
void divide(int x)
{
for (int i = 2; i <= x / i; i ++ )
if (x % i == 0)
{
int s = 0;
while (x % i == 0) x /= i, s ++ ;
cout << i << ' ' << s << endl;
}
if (x > 1) cout << x << ' ' << 1 << endl;
cout << endl;
}3.朴素筛法求质数--O(NlogN)
原理:对于n个数,从2开始枚举,依次将其倍数删去,如果枚举到该数仍存在则该数一定为质数,因为例如一个数p,枚举到它时还存在,说明它不是2~p-1中任何数的倍数,即该数为质数。
int primes[N],cnt;
bool st[N];
筛选出所有数的倍数
void get_primes(int n)
{
for (int i = 2; i <= n; i++)
{
if (st[i]) continue;
primes[cnt++] = i;
for (int j = i + i; j <= n; j += i) st[j] = true;//筛选出i的倍数
}
}4.埃氏筛法求质数--O(loglogN)
埃及筛法就是在朴素筛法的基础上,我们只用将质数的倍数删掉即可,因为一个合数可以写成几个质数的积,那么我们将所有质数的倍数删掉时,所有合数也被删掉了,这样可以将时间复杂度优化到O(nloglogn),可粗略看作O(n)。
优化:通过只筛选质数的倍数即可。
int primes[N],cnt;
bool st[N];
void get_primes(int n)
{
for (int i = 2; i <= n; i++)
{
if (!st[i])
{
primes[cnt++] = i;
for (int j = i + i; j <= n; j += i)
st[j] = true;
}
}
}5.线性筛法求质数O(N)
对于某一个合数n,其只会被自己的最小质因子给筛掉。
int primes[N],cnt;
bool st[N];
void get_primes(int n) {
for(int i = 2; i <= n; i++) {
if(!st[i]) primes[ctn++] = i;
for(int j = 0; primes[j] <= n / i; j++) {
st[primes[j] * i] = true;
// 当下面的if条件成立时, primes[j]一定是i的最小质因子
if(i % primes[j] == 0) break;
}
}
}
6.欧拉筛法O(N)
int i, j, num=1;
memset(u, true, sizeof(u));
for (i=2; i<=n; i++){ //顺序分析整数区间的每个数
if (u[i]) su[num++]=i; //将筛中最小数送入素数表
for (j=1; j<num; j++) { //搜索素数表的每个数
if (i*su[j]>n) break; //若i与当前素数的乘积超出范围,则分析下一个整数i
u[i*su[j]]=false; //将i与当前素数的乘积从筛子中筛去
if (i%su[j]==0) break; //若当前素数为i的最小素因子,则分析下一个整数i
}
}
欧拉筛法证明如下:
设合数𝑛最小素因子为𝑝,它的另一个大于𝑝的素因子为𝑝′,令𝑛=𝑝𝑚=𝑝′𝑚′。
观察上面程序片段,可以发现𝑗循环到素因子𝑝时,合数𝑛第一次被标记(若循环到𝑝之前已经跳出循环,说明𝑛 有更小的素因子)。若也被𝑝′标记,则是在这之前(因为𝑚′<𝑚),考虑𝑖循环到𝑚′,注意到𝑛=𝑝𝑚=𝑝′𝑚′且𝑝和𝑝′为不同的素因子,因此𝑝|𝑚′,所以当𝑗循环到素因子𝑝后结束,不会循环到𝑝′,这就说明不会被𝑝′筛去。
二、约数
1.试除法求所有约数--O(sqrt(N))
原理:假设p是x的一个约数,那么x/p一定也是它的约数,所以只需枚举2 到 sqrt(n)的约数,并且可以直接通过运算获得sqrt(n) 之后对应的那个约数。
vector<int> get_divisors(int x)
{
vector<int> res;
for (int i = 1; i <= x / i; i ++ )
if (x % i == 0)
{
res.push_back(i);
if (i != x / i) res.push_back(x / i);
}
sort(res.begin(), res.end());
return res;
}2.试除法求所有约数之和
vector<int> get_divisors(int x)
{
vector<int> res;
for (int i = 1; i <= x / i; i ++ )
if (x % i == 0)
{
res.push_back(i);
if (i != x / i) res.push_back(x / i);
}
sort(res.begin(), res.end());
return res;
}3.约数个数和约数之和
unordered_map<int, int> primes;
//求约数个数
void get_divisors_numbers(int x)
{
for(int i=2;i<=x/i;i++)
while (x % i == 0)
{
x /= i;
primes[i]++;
}
if (x > 1) primes[x]++;
LL res = 1;
for (auto prime : primes) res = res * (prime.second + 1)%mod;
cout << res << endl;
}unordered_map<int, int> primes;
//求约数之和
void get_divisors_sumNumbers(int x)
{
for(int i=2;i<=x/i;i++)
while (x % i == 0)
{
x /= i;
primes[i]++;
}
if (x > 1) primes[x]++;
LL res = 1;
for (auto prime : primes) {
int p = prime.first, a = prime.second;
LL t = 1;
while (a--) t = (t * p + 1) % mod;
res = res * t % mod;
}
cout << res << endl;
}
4.欧几里得算法
原理:辗转相除法原理是设两数为a、b(a>b),用gcd(a,b)表示a, b的最大公约数,r=a(mod b)为a除以b的余数,k为a除以b的商,即a÷b=k.....r。辗转相除法即是要证明gcd(a,b)=gcd(b, r)。辗转相除法,又名欧几里德算法。

int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}三、欧拉函数

1.求欧拉函数 O(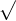 n)
n)
int phi(int x)
{
int res = x;
for (int i = 2; i <= x / i; i ++ )
if (x % i == 0)
{
res = res / i * (i - 1);
while (x % i == 0) x /= i;
}
if (x > 1) res = res / x * (x - 1);
return res;
}2.线性筛法求欧拉函数
- 质数i的欧拉函数即为phi[i] = i - 1:1 ~ i−1均与i互质,共i−1个。
- phi[primes[j] * i]分为两种情况:
- ① i % primes[j] == 0时:primes[j]是i的最小质因子,也是primes[j] * i的最小质因子,因此1 - 1 / primes[j]这一项在phi[i]中计算过了,只需将基数N修正为primes[j]倍,最终结果为phi[i] * primes[j]。
- ② i % primes[j] != 0:primes[j]不是i的质因子,只是primes[j] * i的最小质因子,因此不仅需要将基数N修正为primes[j]倍,还需要补上1 - 1 / primes[j]这一项,因此最终结果phi[i] * (primes[j] - 1)。
void get_eulers(int n)
{
phi[1] = 1;
for (int i = 2; i <= n; i++)
{
if (!st[i])
{
primes[cnt++] = i;
phi[i] = i - 1;
}
for (int j = 0; primes[j] <= n / i; j++)
{
st[primes[j] * i] = true;
if (i % primes[j] == 0)
{
phi[primes[j] * i] = phi[i] * primes[j];
break;
}
phi[primes[j] * i] = phi[i] * (primes[j] - 1);
}
}
}
四、快速幂
1.求快速幂

typedef long long LL;
LL qmi(int a, int b, int p)
{
LL res = 1 % p;
while (b)
{
if (b & 1) res = res * a % p;
a = a * (LL)a % p;
b >>= 1;
}
return res;
}
2.快速幂求逆元
- 当n为质数时,可以用快速幂求逆元:
a / b ≡ a * x (mod n)
两边同乘b可得 a ≡ a * b * x (mod n)
即 1 ≡ b * x (mod n)
同 b * x ≡ 1 (mod n)
由费马小定理可知,当n为质数时
b ^ (n - 1) ≡ 1 (mod n)
拆一个b出来可得 b * b ^ (n - 2) ≡ 1 (mod n)
故当n为质数时,b的乘法逆元 x = b ^ (n - 2)
- 当n不是质数时,可以用扩展欧几里得算法求逆元:
a有逆元的充要条件是a与p互质,所以gcd(a, p) = 1
假设a的逆元为x,那么有a * x ≡ 1 (mod p)
等价:ax + py = 1
exgcd(a, p, x, y)
import java.util.*;
import java.io.*;
public class Main{
static BufferedReader bf=new BufferedReader(new InputStreamReader(System.in));
static PrintWriter pw=new PrintWriter(System.out);
static long qmi(long a,long b,long p){
long res=1%p;
while(b!=0){
if((b&1)==1) res=res*a%p;
a=a*a%p;
b>>=1;
}
return res;
}
public static void main(String[] args)throws Exception{
int n=Integer.valueOf(bf.readLine());
while(n-->0){
String[] ss=bf.readLine().split(" ");
long a=Integer.valueOf(ss[0]);
long p=Integer.valueOf(ss[1]);
if(a%p==0)
pw.println("impossible");
else
pw.println(qmi(a,p-2,p));
}
pw.flush();
}
}五、扩展欧几里得算法

模板一:
void exgcd(int a,int b,int &x,int &y){
if(!b){ //若b=0时
x=1,y=0;
return ;
}
else{ //b!=0时
exgcd(b,a%b,x,y); //递归到下一层
int t=x; //返回时执行
x=y;
y=t-a/b*y;
}
}模板二:
int exgcd(int a, int b, int &x, int &y)
{
if (!b)
{
x = 1, y = 0;
return a;
}
int d = exgcd(b, a % b, y, x);
y -= a / b * x;
return d;
}六、中国剩余定理
- 对于每两个式子(我们考虑将其合并):
x≡m1(% a1)
x≡m2(% a2)
能够推出
x=k1∗a1+m1
x=k2∗a2+m2
进一步:
k1∗a1+m1=k2∗a2+m2
移项得:
k1∗a1−k2∗a2=m2−m1
① k1∗a1+k2∗(−a2)=m2−m1
我们已知a1,m1,a2,m2,可以用扩展欧几里得算法算出一个k′1,k′2
使得:
k′1∗a1+k′2∗(−a2)=gcd(a1,−a2)
无解判断:
若gcd(a1,−a2)/m2−m1,则无解。我们设d=gcd(a1,−a2),y=(m2−m1)d承接上文,我们只需让k1,k2
分别扩大y倍,则可以找到一个k1,k2
满足①式:
k1=k′1∗y,k2=k′2∗y
找到最小正整数解
②k1=k1+k∗a2d
k2=k2+k∗a1d
这里带入后即可证明与1式相同。要找一个最小的非负整数解,我们只需要让
k1=k1% abs(a2d)
k2=k2% abs(a1d)
即可找到当前最小的k1,k2的解,即此时的k为0。
等效替代:
由②式带入新的x为:
x=(k1+k∗a2d)∗a1+m1
=k1∗a1+m1+k∗a2∗a1d
=k1∗a1+m1+k∗lcm(a1,a2)③
这里,k都为0了,为什么还要算呢?
因为这只是前两个式子得最小k,有可能遇到下一个式子后面被迫要扩大
在③中,我们设a0=lcm(a1,a2),m0=k1∗a1+m1
那么:③ x=k∗a0+m0
x=k∗a0+m0=k3∗(−a3)+m3
,那么问题又回到了第一步。
#include <bits/stdc++.h>
typedef long long LL;
//计算机中对于%与数学中不同,所以需要经过处理
inline LL mod(LL a,LL b)
{
return (a%b+b)%b;
}
LL exgcd(LL a,LL b,LL& x,LL &y)
{
if(b==0)
{
x=1,y=0;
return a;
}
LL d=exgcd(b,a%b,y,x);
y-=a/b*x;
return d;
}
int main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);std::cout.tie(nullptr);
int n;
std::cin>>n;
LL a1,m1;
std::cin>>a1>>m1;
bool flag=true;
for(int i=1;i<n;i++){
LL a2,m2;
std::cin>>a2>>m2;
LL k1,k2;
LL d=exgcd(a1,a2,k1,k2);
if((m2-m1)%d){//如果有解,此时(m2-m1)%d一定是等于0的
flag=false;
break;
}
k1*=(m2-m1)/d;//特解
LL t=a2/d;
k1=mod(k1,t);//使k1取到最小正整数解
m1=a1*k1+m1;
a1=std::abs(a1/d*a2);
}
if(flag) std::cout<<mod(m1,a1)<<std::endl;
else std::cout<<-1<<std::endl;
return 0;
}
























 8601
8601











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










