【动态规划算法】-简单多状态题型（11-18题）

本文链接：https://blog.csdn.net/qq_69369227/article/details/131619188

本文通过多个LeetCode题目，详细讲解了动态规划中的简单多状态类型题目，包括按摩师、打家劫舍II、删除并获得点数等，分析了状态表示、动态规划步骤和代码实现，帮助读者理解这类题目的解题思路和方法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

💖作者：小树苗渴望变成参天大树🎈
🎉作者宣言：认真写好每一篇博客💤
🎊作者gitee:gitee✨
💞作者专栏：C语言,数据结构初阶,Linux,C++ 动态规划算法🎄

如果你喜欢作者的文章，就给作者点点关注吧！

文章目录

前言
第十一题:[面试题 17.16. 按摩师](https://leetcode.cn/problems/the-masseuse-lcci/)
第十二题:[213. 打家劫舍 II](https://leetcode.cn/problems/house-robber-ii/)
第十三题:[740. 删除并获得点数](https://leetcode.cn/problems/delete-and-earn/)
第十四题：[剑指 Offer II 091. 粉刷房子](https://leetcode.cn/problems/JEj789/)
第十五题：[309.最佳买卖股票时机含冷冻期](https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-cooldown/)
第十六题：[714. 买卖股票的最佳时机含手续费](https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/)
第十七题：[123. 买卖股票的最佳时机 III](https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iii/)
第十八题：[188. 买卖股票的最佳时机 IV](https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iv/)

前言

这篇博主花了好几天讲动态规划中的简单多状态类型的题目，难度也是从低到高，理解方面和之前也有不同，我会以三步给大家讲解，**题目解析，动态规划步骤，代码实现，**来解决问题，简单多状态表明我们我们讲题目进行多状态分析，然后进行简单化，之前都是一种状态，所以相对来说好理解一些，这篇说到的题型你都理解了，就会发现简单多状态就那么回事

第十一题:面试题 17.16. 按摩师

题目解析：
在这里插入图片描述

通过题解，我们选出数组中符合规则元素和的最大值就行了。

动态规划的步骤

状态表示：经验+题目要求
以i位置为结尾：
f[i]表示：从起点到达i位置，选择i位置时的最大值
g[i]表示：从起点到达i位置，不选择i位置，而是选择前面一位时的最大值

我们发现此位置不像是之前只有一种状态，这题有两种状态，这就是多状态

状态转移方程：以最近的状态来算此状态。

f[i]=g[i-1]+nums[i];

在这里插入图片描述

g[i]=max(f[i-1],g[i-1])

初始化：保证数组不越界，此题不需要创建虚拟节点，初始化非常简单第0个位置选还是不选的问题
选：f[0]=nums[0],不选：g[0]=0;
填表顺序：从左往右，两表同时填写
返回值
就是返回选的值大，还是不选的值大max(f[n-1],g[n-1])

代码实现：

class Solution {
   
public:
    int massage(vector<int>& nums) {
   
        //1.创建两个状态的dp表
        
        int n=nums.size();
        if(n==0)return 0;
        vector<int> f(n);//选
        auto g=f;//不选
        f[0]=nums[0];//初始化
        for(int i=1;i<n;i++)
        {
   
            f[i]=g[i-1]+nums[i];
            g[i]=max(g[i-1],f[i-1]);
        }
        return max(f[n-1],g[n-1]);
    }
};

运行效果：
在这里插入图片描述

这题因为有多种状态，所以我们要去分析不同状态对应的情况，经验还是适用的。，我们来看下一题

在这里插入图片描述
这个题目按照正常思路是不好做下去的，因为我们任意位置开始选数，把对应的+1和-1位置的值删除，就说明你选择了这个位置，这个数的前一个数和下一个数你都选不了，来看图解：

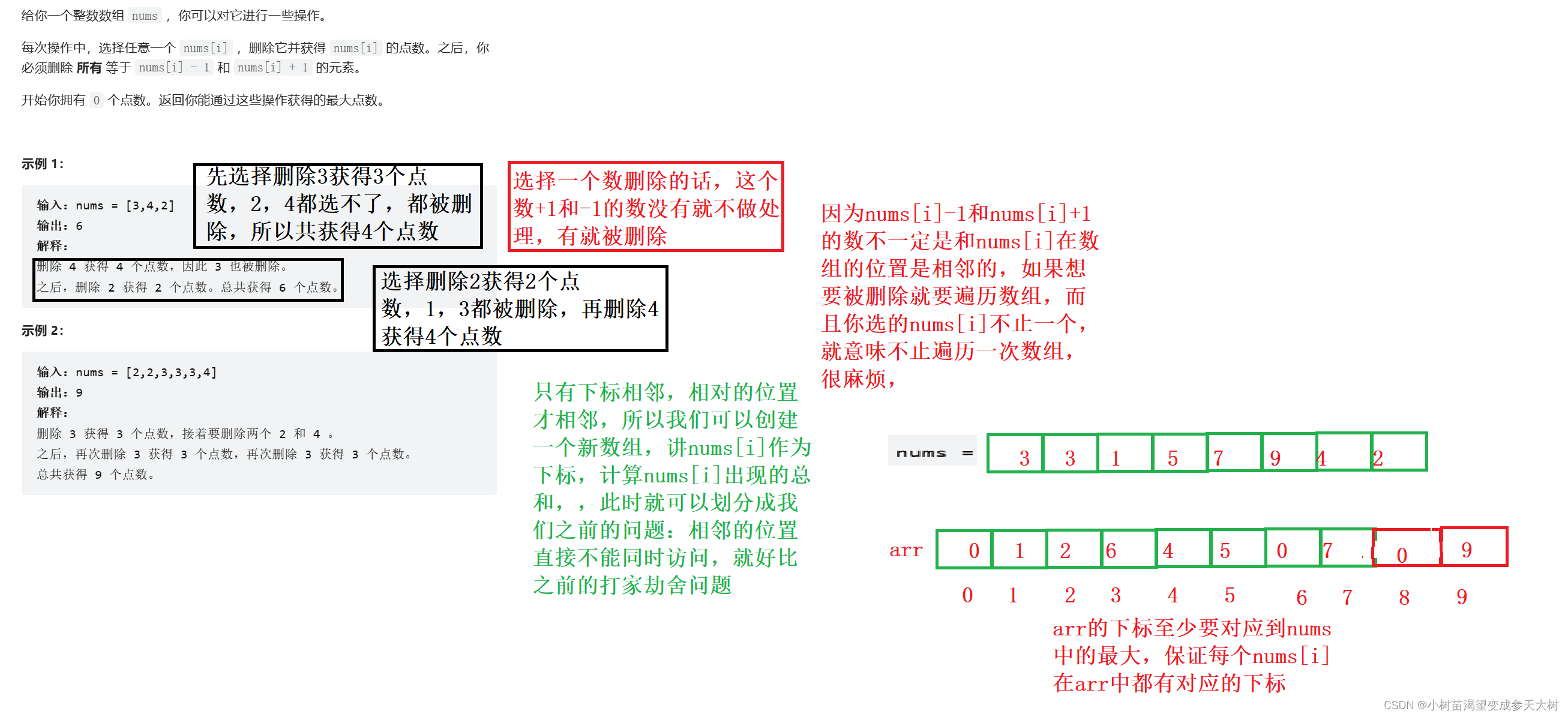
大家要是看过我的计数排序那篇博客，应该理解我说的什么意思，这个问题就转换成上题中的子问题，相邻的两个位置不能选，选择删除arr[i]位置的值，点数就加上arr[i]，就相当于选择了nums[i]就等于arr[i]中的i,然后再arr中i-1位置和i+1位置的值就不能选，就相当于nums[i]-1和nums[i]+1的值被删除了。