题解 - 折纸

题目描述

小爱手中有一张矩形纸张，他想把这张纸分成若干正方形纸片，具体分法如下:
。第1步:小爱会先确定纸张的长宽，假设短边长度为几，长边长度为m，
。第2步:小爱会将短边沿直角平分线对折后剪去，从而得到一个nxn的方形纸片。
。第3步:若还有剩余，小爱会将剩余的长宽为几*(m-n)的纸张作为现有纸张，代入第一步后重复之前过
程，直至没有之后纸张剩余为止。
请问按如上操作，小爱最终会得到几张方形纸片?
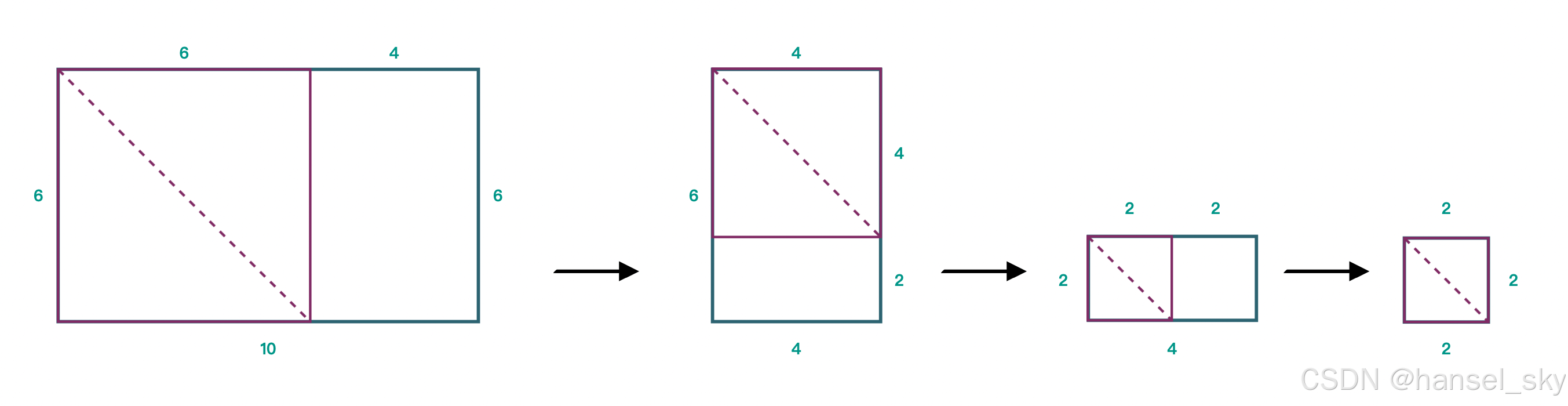
例如:一开始，小爱有一张 10 x6 的纸张，按他的分割方法，最终他可以获得 4 张方形纸片，具体过程如下图所示:

输入格式
输入共两个正整数，表示初始矩形纸张的长宽 m,n
输出格式
输出题目所求能获得的矩形个数
数据范围
。对于 30% 的数据，1< n,m< 100
。对于 60% 的数据，1≤ n,m < 107
。对于 100% 的数据，1 ≤n,m < 1013

样例数据
输入:
10 6
输出:
4

分析

知识点：数学

解题思路：

对于长边 $n$ ，它被取 $w=\lfloor n/m\rfloor$ 后才会变成短边，剩余 $n1=n-w\ast m=nmodm$

所以对于一个对边，它对答案的贡献为 $n/m$ 然后令 $n=n\%m$

容易发现这个过程本质就是gcd的过程，则时间复杂度一致

复杂度 $O(logn)$

代码

#include<bits/stdc++.h>
#define LL long long
using namespace std;
LL n,m;
int main(){
	cin>>n>>m; LL cnt=0;
	while(m){
		cnt+=n/m; n=n%m;
		swap(n,m);
	}
	cout<<cnt<<endl;
}