手撕排序算法（二）——堆排序

我之前粗略的写了一下，但是阅读量不高，此篇文章是我讲过精心修改后得出的，感谢大家一直以来的支持。

本期内容难度较高，我会先和大家一起在理论上探讨堆排序的原理，最后跟大家一起以C语言为基础实现代码。在阅读本片文章前我建议大家本着一遍可能难以理解的心态去阅读，因为这个知识点融合了二叉树和排序的内容，所以对基础要求较高，希望本篇文章能够帮助到大家！

堆排序的性质

性质：在完全二叉树中，子结点的键值或索引总是小于（或者大于）它的父节点

如图：便是在一组数中堆排序（大顶堆）的最终形态。

大顶堆

堆排序的原理

实现逻辑：

① 先将初始的R[0…n-1]建立成最大堆，此时是无序堆，而堆顶是最大元素。

② 再将堆顶R[0]和无序区的最后一个记录R[n-1]交换，由此得到新的无序区R[0…n-2]和有序区R[n-1]，且满足R[0…n-2].keys ≤ R[n-1].key

③ 由于交换后新的根R[1]可能违反堆性质，故应将当前无序区R[1..n-1]调整为堆。然后再次将R[1..n-1]中关键字最大的记录R[1]和该区间的最后一个记录R[n-1]交换，由此得到新的无序区R[1..n-2]和有序区R[n-1..n]，且仍满足关系R[1..n-2].keys≤R[n-1..n].keys，同样要将R[1..n-2]调整为堆。

④ 直到无序区只有一个元素为止。

简单点就是如下图：

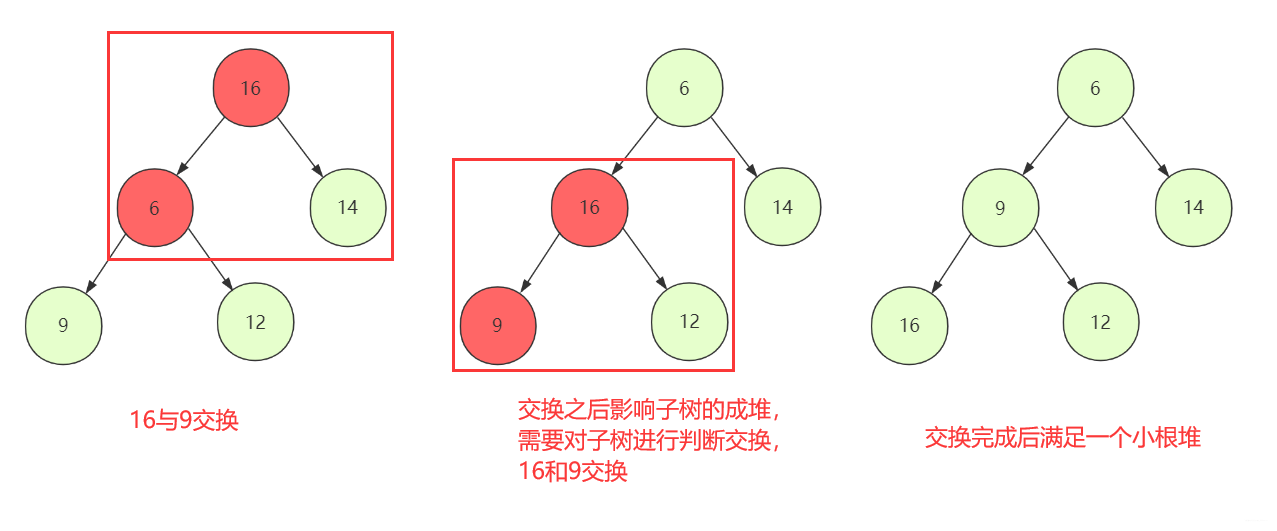
这是小顶堆的实现。

堆实现的要点

实现堆排序需要解决两个问题：

1、如何由一个无序序列建成一个堆？
2、如何在输出堆顶元素之后，调整剩余元素成为一个新的堆？

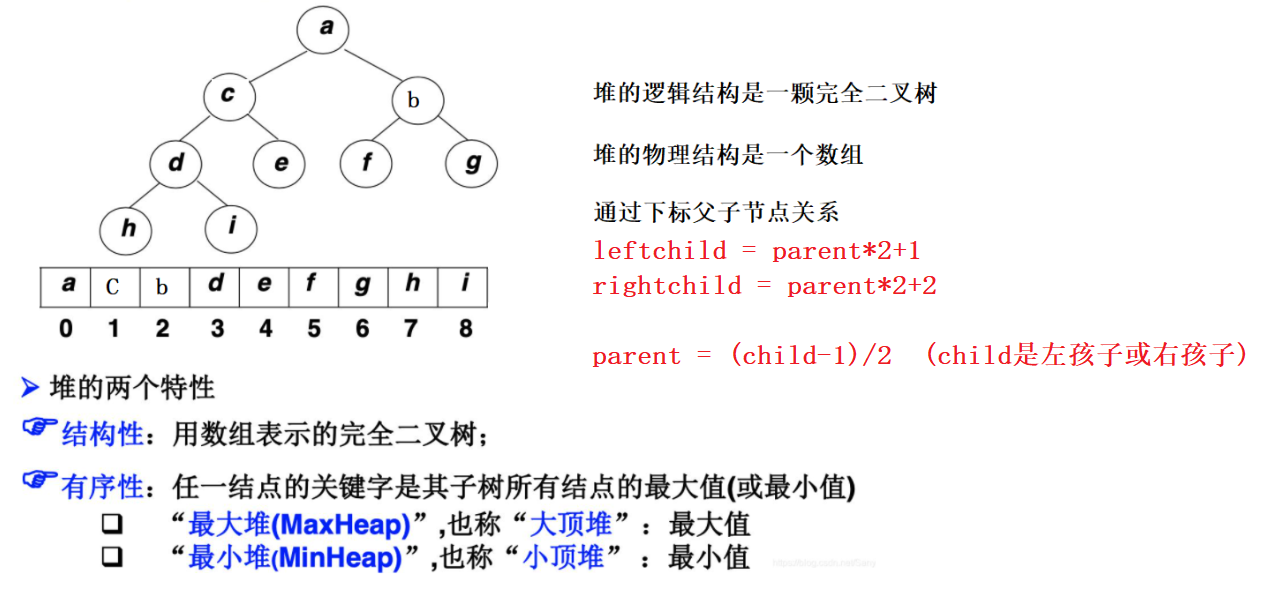
注意：如果不满足结构性和有序性那么就不能够实现堆。

由一个无序序列建成一个堆之前，如何满足堆的有序性呢？就是建堆的过程。

建堆

建堆又叫有序性的实现。

我们可以思考一下，如果我们排升序是大堆还是小堆 —— 大堆，为什么呢？

选择排序，本质就是通过堆来选数,如果是建小堆，最小数在堆顶，已经被选出来了。那么在剩下的数中再去选数，但是剩下树结构都乱了，需要重新建堆才能选出下一个数，建堆的时间复杂度是0(N),那么这样不是不可以，但是堆排序就没有效率优势了。

建堆的过程：

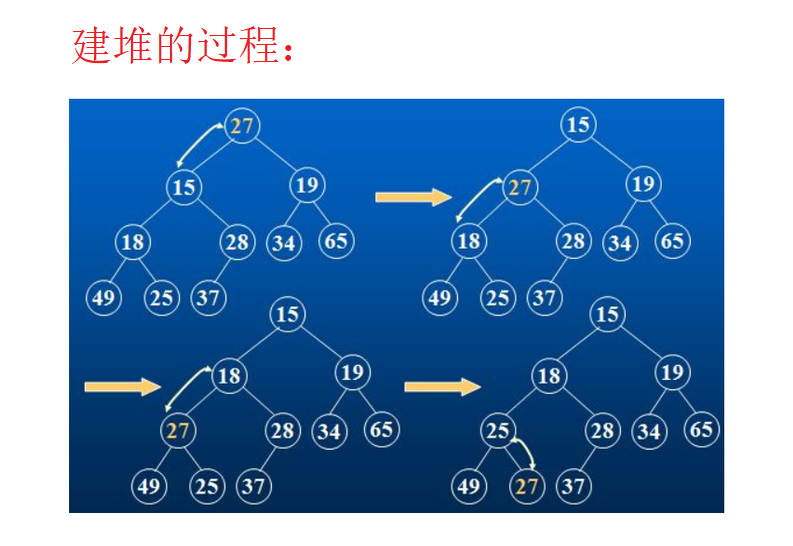
建堆的实现：

那么我们将理论转换为代码就是做一个向下调整函数。

//向下调整
void AdjustDwon(int* a, int n, int root)
{
    int parent = root;
    int child = parent * 2 + 1; // 默认是左孩子
    while (child < n)
    {
        // 1、选出左右孩子中大的那一个
        if (child + 1 < n && a[child + 1] > a[child])
        {
            child += 1;
        }

        if (a[child] > a[parent])
        {
            Swap(&a[child], &a[parent]);
            parent = child;
            child = parent * 2 + 1;
        }
        else
        {
            break;
        }
    }
}

堆排序

有同学可能会觉得网络上的图太麻烦了，那我们就自己做一个简单的：

简而言之就是：

第一个和最后一个交换，把他不看做堆里面前n-1个数向下调整，选出次大的数，再跟倒数第二个位置交换

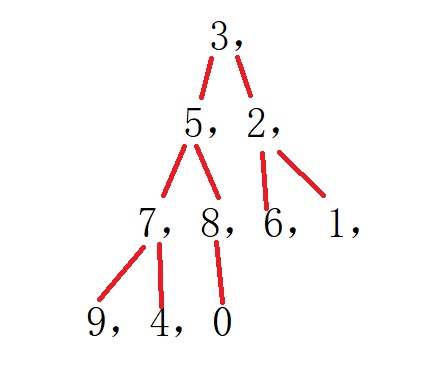
堆排序

那么左右子树不是小堆，就不能直接使用向下调整算法了!怎么办?倒着从最后一颗子树开始调。

再分析倒着走，也子不需要调，从倒数最后一个非叶子的子树开始调也就是8

有了基础了解以后，我们在试着分析一下上图，其实还是比较清晰的。

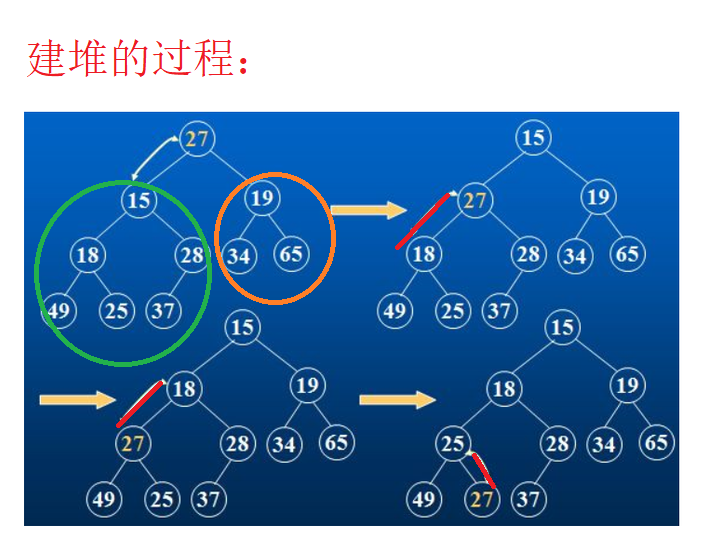
我们试着实现一下代码：

// 堆排序
void HeapSort(int* a, int n)
{
    //建堆
    int i = 0;
    for (i = (n - 1 - 1) / 2; i >= 0; i--)
    {
        AdjustDwon(a, n, i);
    }
    //排升序是大堆还是小堆  ——  大堆
    int end = n - 1;
    while (end > 0)
    {
        Swap(&a[0], &a[end]);
        AdjustDwon(a,end, 0);
        end--;    
    }
}

测试

到底能不能行，我们测试见真章。

void TestInsertSort1()
{
    int a[] = { 2,1,5,6,9,3,7,8 };
    HeapSort(a, sizeof(a) / sizeof(int));
    Print(a, sizeof(a) / sizeof(int));
}

int main()
{
    TestInsertSort1();
    return 0;
}

结果为：

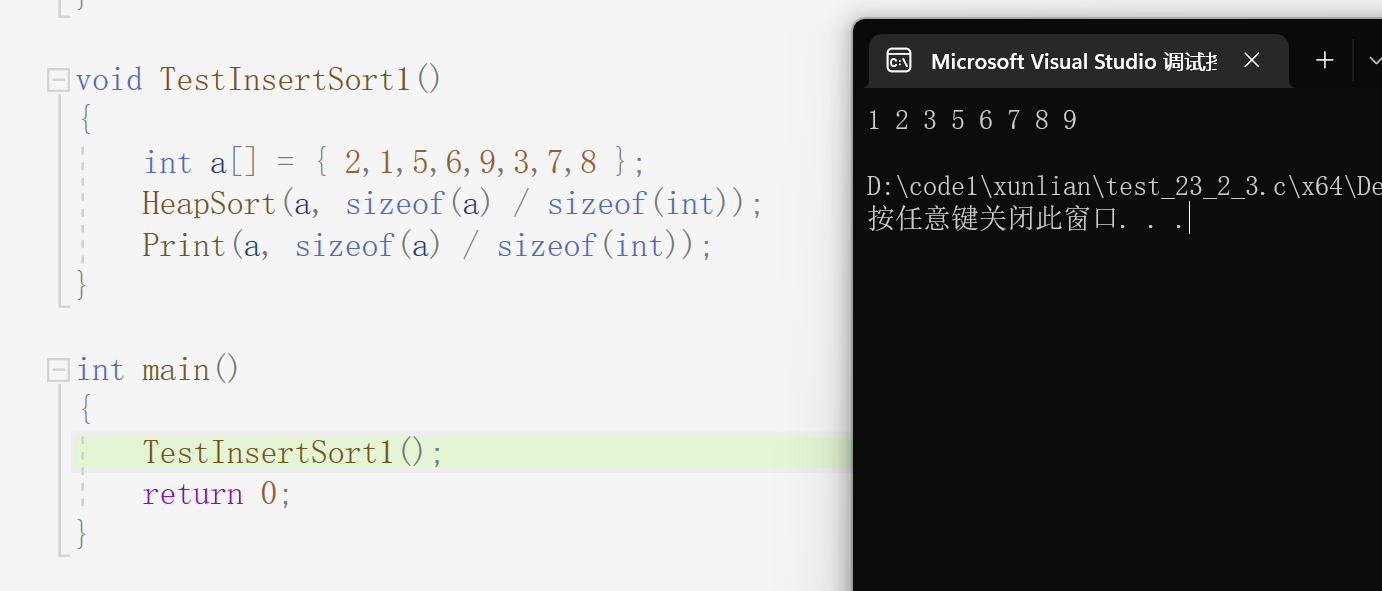
这样我们就实现了升序，感兴趣的可以试着实现降序。

降序代码：

//降序
void AdjustDwon(int* a, int n, int root)
{
    int parent = root;
    int child = parent * 2 + 1; // 默认是左孩子
    while (child < n)
    {
        // 1、选出左右孩子中大的那一个
        if (child + 1 > n && a[child + 1] < a[child])
        {
            child += 1;
        }

        if (a[child] < a[parent])
        {
            Swap(&a[child], &a[parent]);
            parent = child;
            child = parent * 2 + 1;
        }
        else
        {
            break;
        }
    }
}

降序结果为：

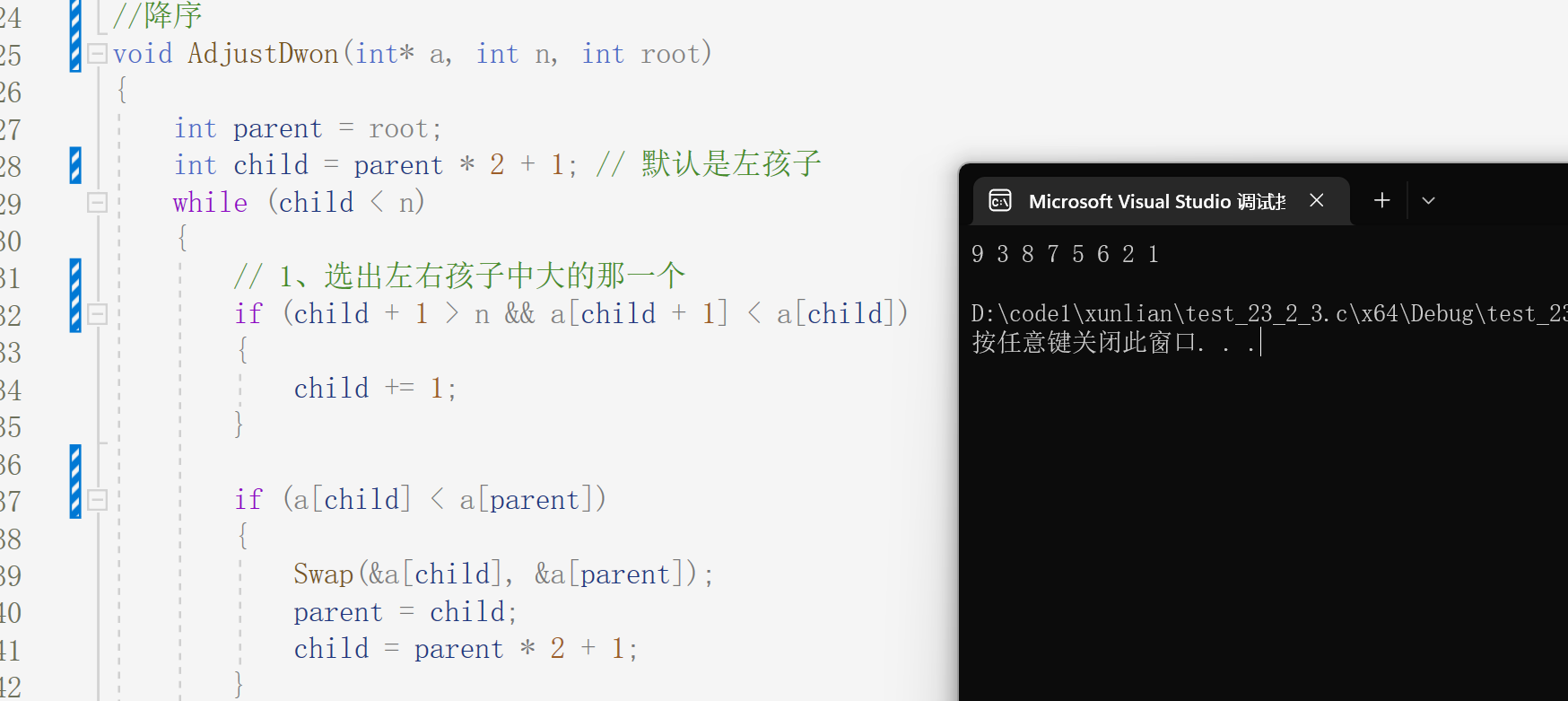
总结

我们用C语言成功实现了堆排序，但是本篇内容难度较高，建议大家可以多看几遍。我初学的时候也对这个堆排序犯迷糊，但是多学几遍还是可以学会的。希望通过本篇的学习大家能够有所收获。

欢迎大家点赞和收藏哦！