算法--数论二

高斯消元

高斯消元求线性方程组

用途

这个算法可以以n的三次方的时间复杂度来求一个线性方程组的解（即x1，x2，x3，…，xn）
但是同时要注意，方程组的解有三种情况，上图

例子：

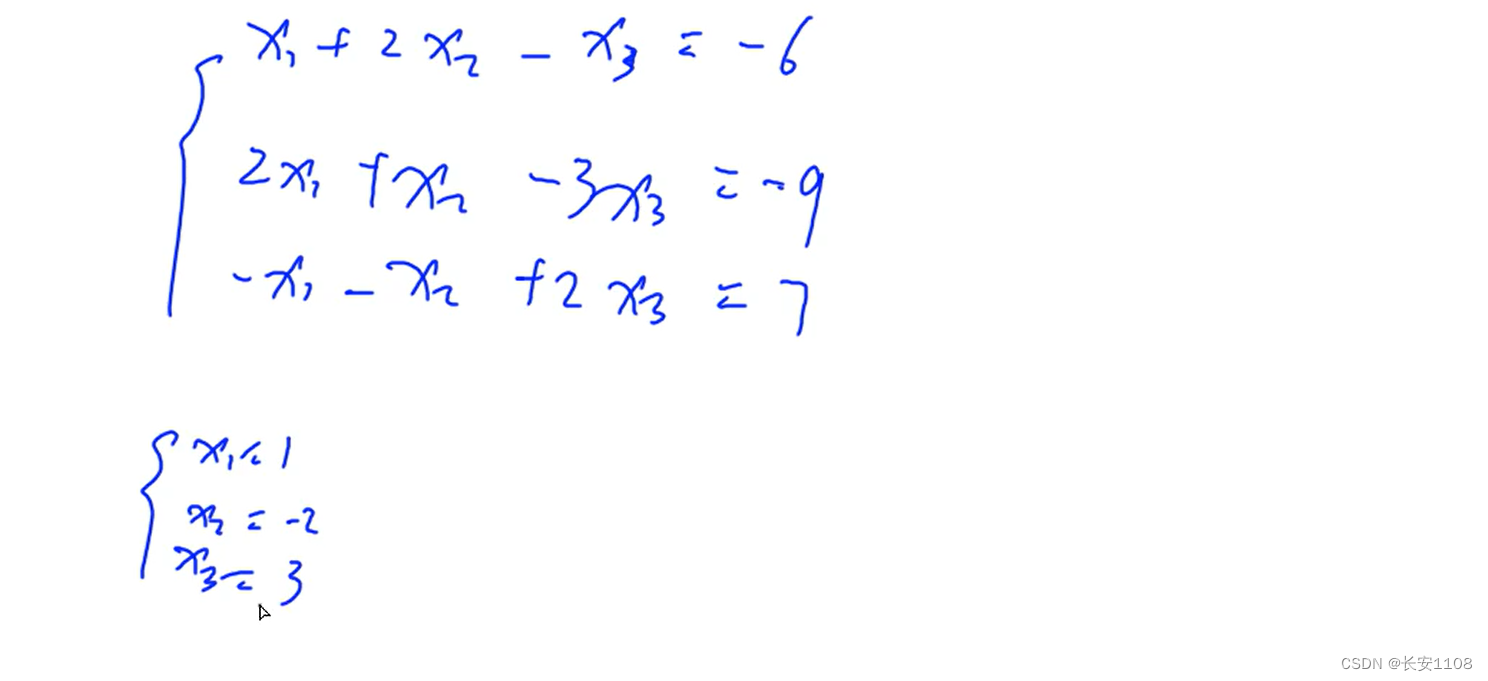
输入n*（n+1）个数，其中每一行包含n个系数以及一个等式右边的答案，一共有n行
最后输出x1到xn

高斯消元的数学思想

将系数抽出来，组成一个矩阵，之后对矩阵做初等行列变化，化为最简阶梯型矩阵，最后化为上三角，如下图所示

关于解的情况，有三种：
在推上三角的过程中
如果最后能化成完美三角形，那就是有唯一解
如果最后出现0=非零，那么就是有矛盾，就是无解
如果最后出现了恒等方程，也就是能消去一个方程，或者说n个未知数，但是只有小于n个解，那么就是无穷解

具体的步骤以及最后的结果：

具体高斯消元的数学思想可以看视频《数学知识（三）》的20-36分钟

例题+代码

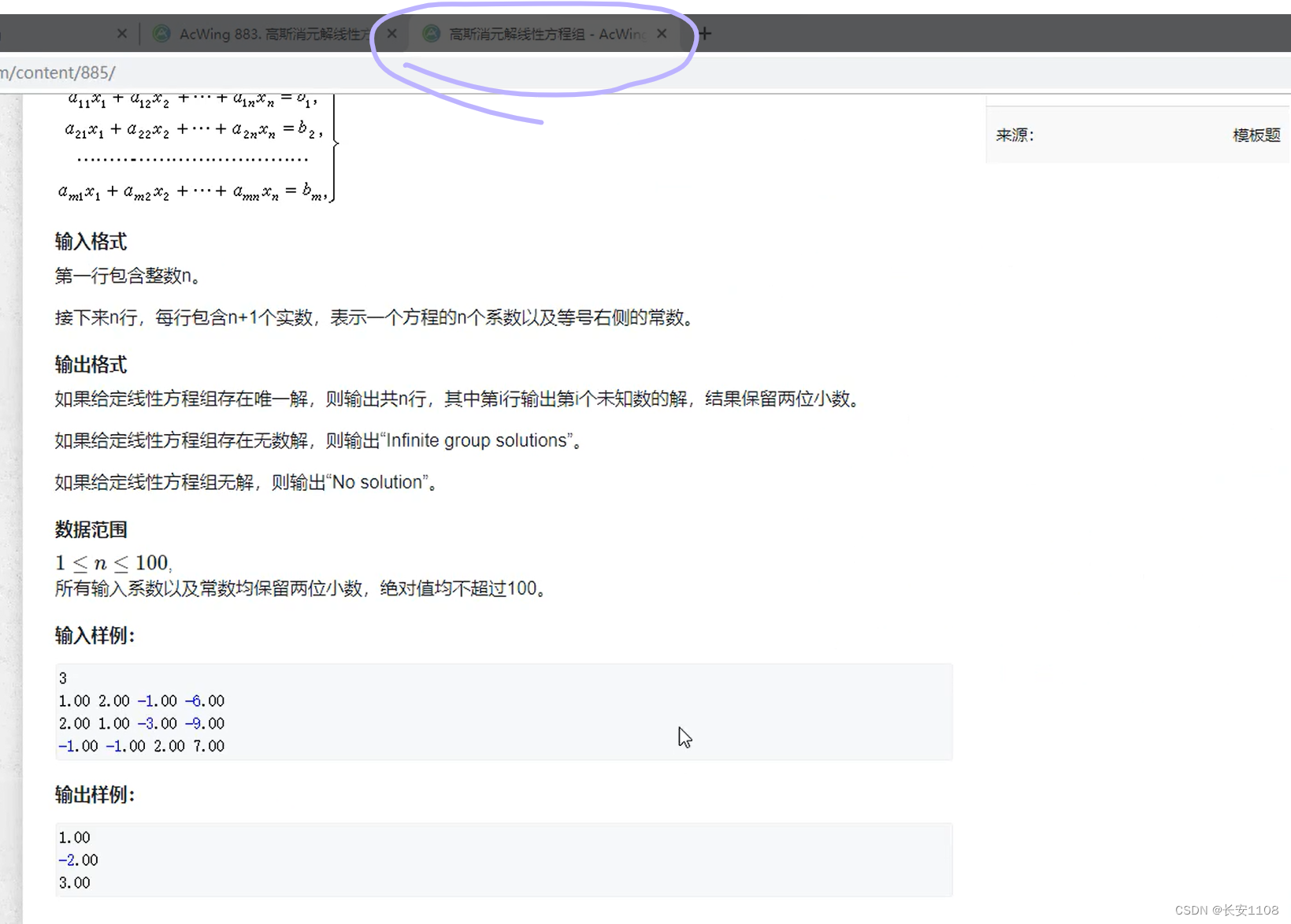
最后的数据都存放在了a[i][n]种，即最后一列的所有行，也就是等式右边的那些值，tips：保留两位小数，%.2lf，在%lf之前加一个.2

数据分析:
定义一个n，表示有几行，也就是有几个解
之后a数组用来存储输入数据，即所有的系数和等式右边的数
eps=1e-6，因为浮点数数据有误差，他的0不是真正的0，而是0.000000…1，所以需要用小于一个特别小的数来表示是0

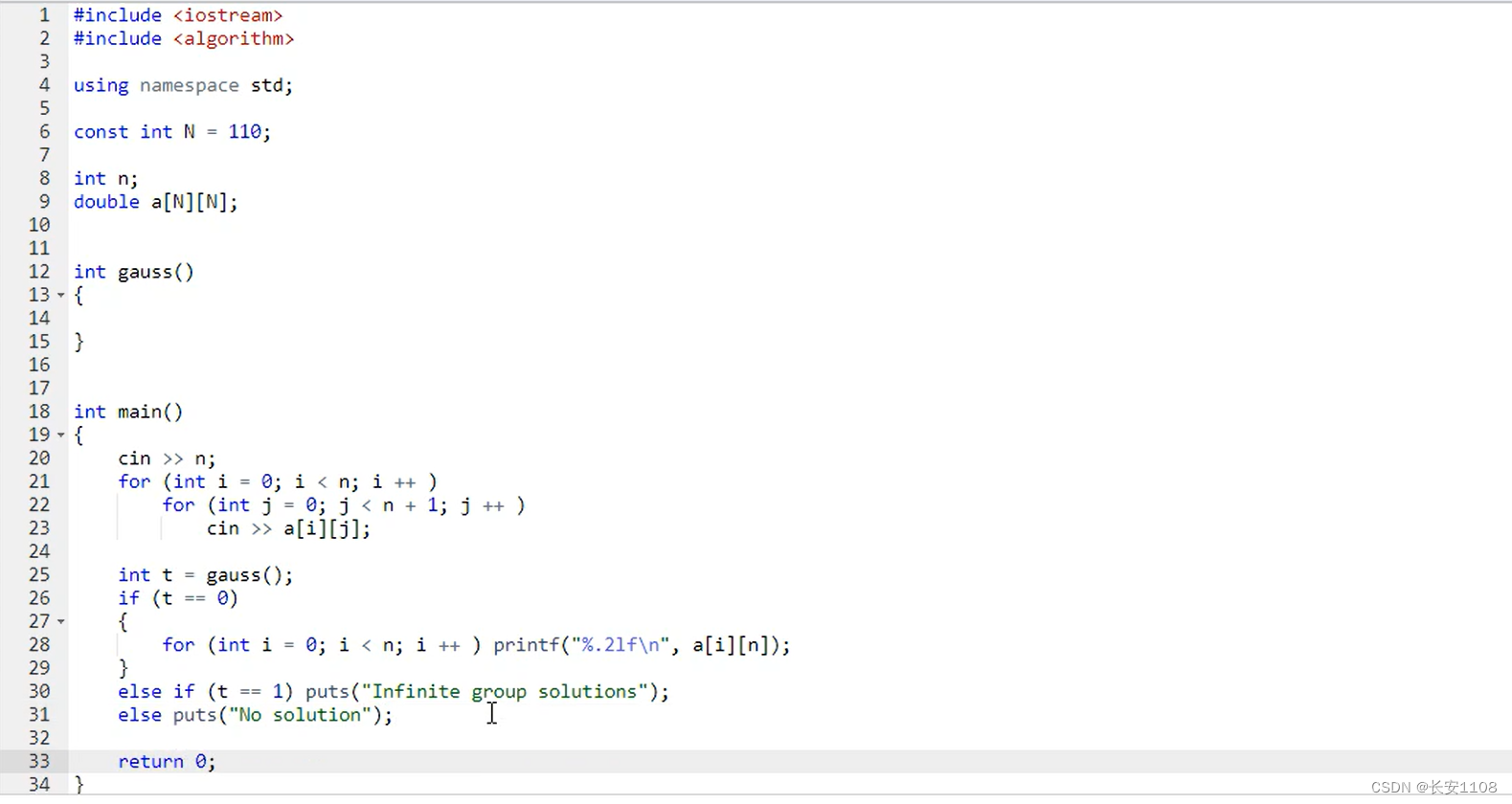
在gauss函数里：
c代表当前列，r代表当前行
之后，for循环中初始化c和r都是0，然后遍历c，（初始化r为0，是用来动态设置当前的“顶行位置”，只有当前这个大的for循环快要结束时，r才会++）
在每一步遍历中，都是在c行下进行的
进行第一步：
先定义一个t，初始化为r，用来存当前列的绝对值最大值数的行号
之后一个for循环，用来找到当前列的绝对值最大的行：i从r开始遍历下面的所有行，如果fabs(a[i][c])>fabs(a[t][c])，那么i就是目前来说最大的行号，将t更新为i。tip：fabs（x），返回x的绝对值，并且是浮点类型，包含头文件cmath
之后拿到 t 之后，特判一下，如果fabs(a[t][c] < eps) 那么就是0，continue一下，因为是0的话就不用其他操作了
进行第二步：（将该行换到最上面）
定义i从c循环到小于等于n，交换a[t][i],a[r][i]
进行第三步：（将该行第一个数变成1）
注意这一步要倒着进行循环，因为每一次操作都要用到a[r][c]，所以要在最后一次循环之前保证a[r][c]是不变的，同时注意此时不再是t行，而是r行，因为第二步时已经换到第一行了
定义i从n到大于等于c，i–，a[r][i] /= a[r][c]
进行第四步：（将下面所有的行的数变成0）
for循环定义i从r+1开始，循环到小于n，因为当前是在r，所以从r+1开始
判断如果a[i][c] >eps，即a[i][c]不是0，再进行后续操作
后续操作：（开始变为0，与第三步思想相同，等式左右同时进行数学变换，使得第c列下面的数都是0）
for循环定义 j 从n到大于等于c，j–
(此时i代表行号，j代表i行目前的列号)
a[i][j] -= a[r][j]*a[i][c]
当前行遍历列的所有的数，都更新为自己减去第一行当前列的数 乘以 当前行第一个数
最后r++；for循环结束

然后判断如果r<n,也就是最后方程数小于解的个数，那么有两种解的情况，
for循环，i 从 r 到 小于n，表示要判断那些没有用到的方程，（i表示行）
之后每次循环判断是否有a[i][n] > eps，即a[i][n]不是0，如果有，就是无解，返回2
for循环结束，返回1，表示有无穷个解
最后如果没有r<n，整个gauss函数返回0即表示有唯一解
但是返回0之前，要对答案进行化简求解，就是上图中的最后一个for循环

求组合数

组合数一（a和b的范围在两千级别）

算法思想

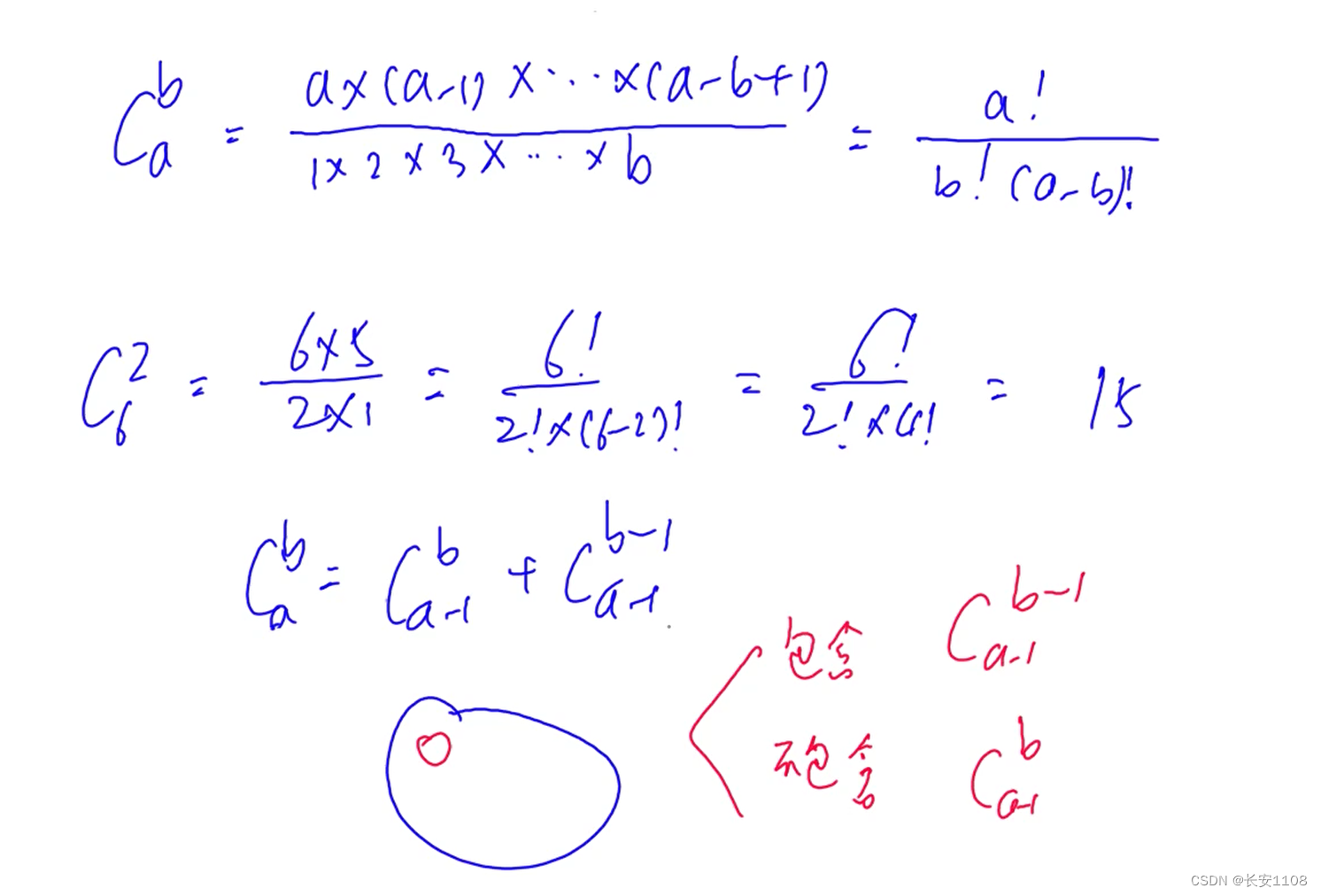
求组合数，用到的是预处理的思路，将所有的情况预处理出来之后，存住，将来用到哪个就查表

预处理：
有一个递推公式，如上图所示。记忆时可以采用这样的思想：在蓝色圈内有所有的苹果，我们圈出来一个A苹果，之后，现在的情况只有“接下来包含这个A苹果”以及“接下来不包含这个A苹果”，包含就是：已经拿了一个A，由于包含A，所以拿走的那个A有效，所以再选的时候从a-1个中选b-1个，不包含就是：已经拿了一个A，但是A无效，所以再选的时候从a-1个中，拿b个

例题+代码

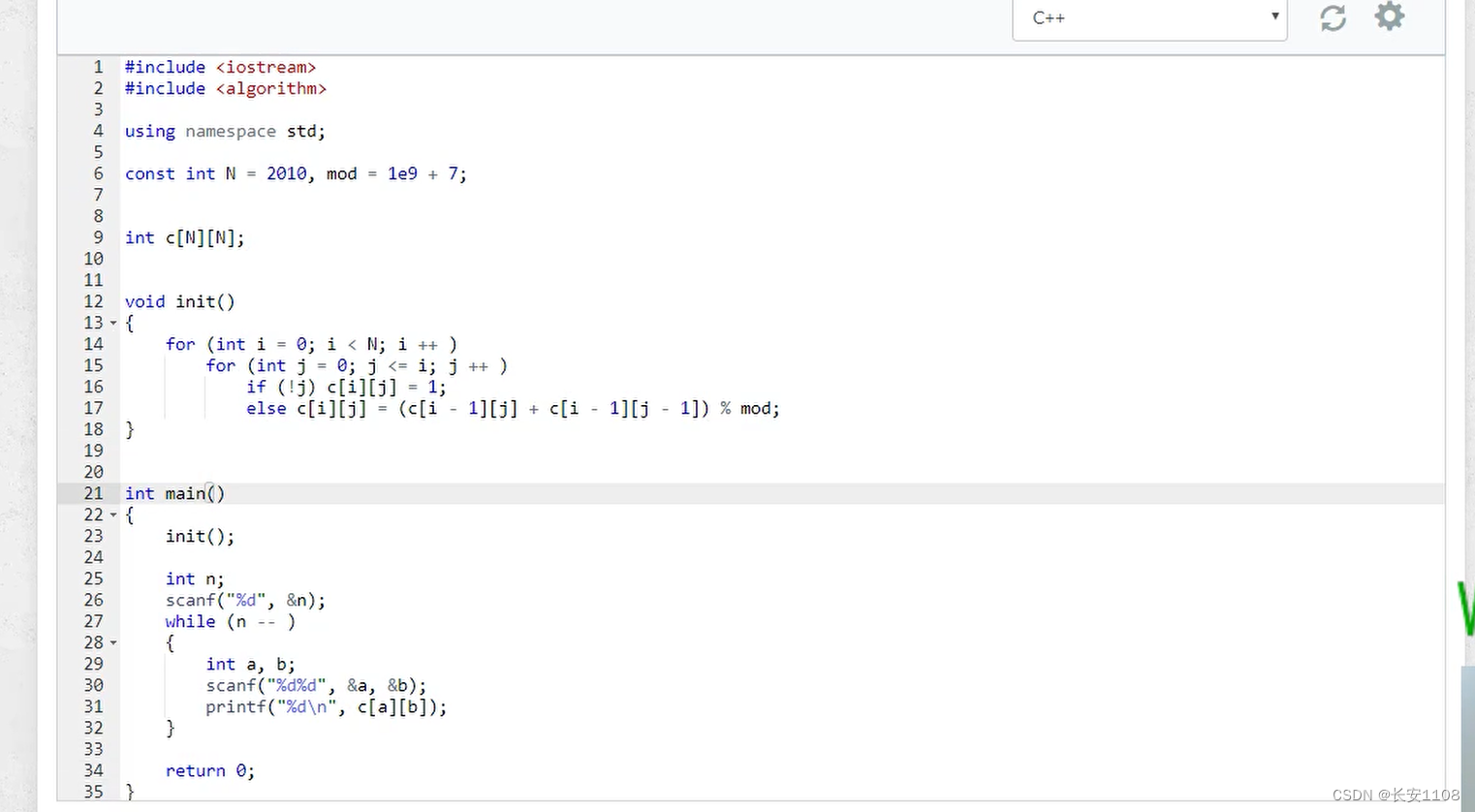
代码解释：
首先定义N=2010，该N是用来表示a，b的最大范围，题目的最大范围是2000，我们最好是再加10的预留量，所以是2010
定义mod=1e9+7，因为数据过大，题目要求结果要模上1e9+7
定义c[N][N]，用来存储预处理的组合数

main函数里，满足题目要求，进行n个查询
但是要先进行初始化，也就是预处理过程
预处理函数中：
两个循环 i 从0到N进行循环，之后 j 从0到小于等于 i 进行循环 （i表示c的下标，j表示c的上标）
之后，特判特殊情况：当 j 为0时，c的值是1
除此之外其他的都使用那个通项公式，即 c[i][j]=c[i-1][j] + c[i-1][j-1]，但是这里考虑到题目的要求，最后%上mod

预处理完之后，题目想要查询哪个，就输出哪个即可

组合数二（a和b的范围在十万级别）

算法思想

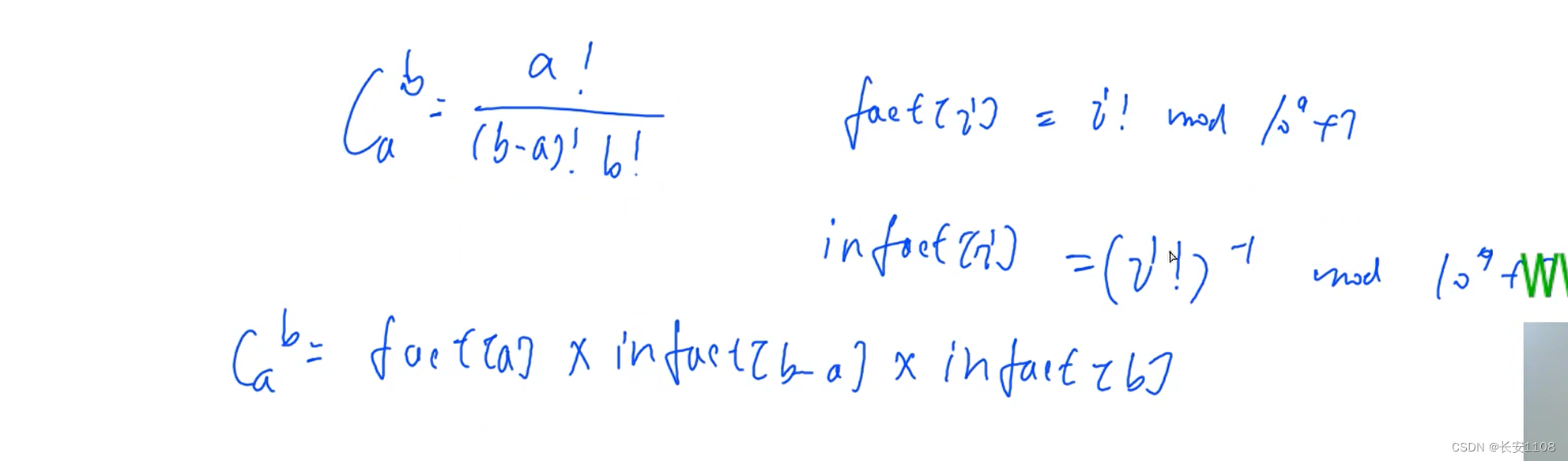
当a，b的数据范围来到十万级别的时候，我们进行预处理时，就要处理所有数的阶乘，以及所有数的阶乘的逆元，之所以需要用到逆元，是因为下图所示，除法无法进行取模操作，只能转换为逆元乘法才可以，且可以避免精度缺失

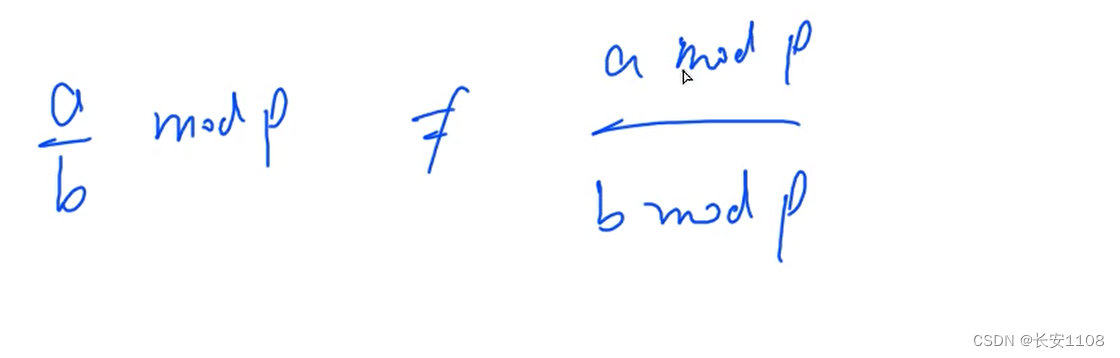
例题+代码（求C时使用阶乘公式）

要注意：强制类型转换可以由低向高转，且他具有很高的优先级，并且对一个变量执行强制类型转换之后，原变量的类型和值都不会变，仅限于那次转换。并且编译器还有自动转换（隐式转换），即在一次运算中，会自动将所有的运算数转为最高级（包括那个接收结果的变量）。

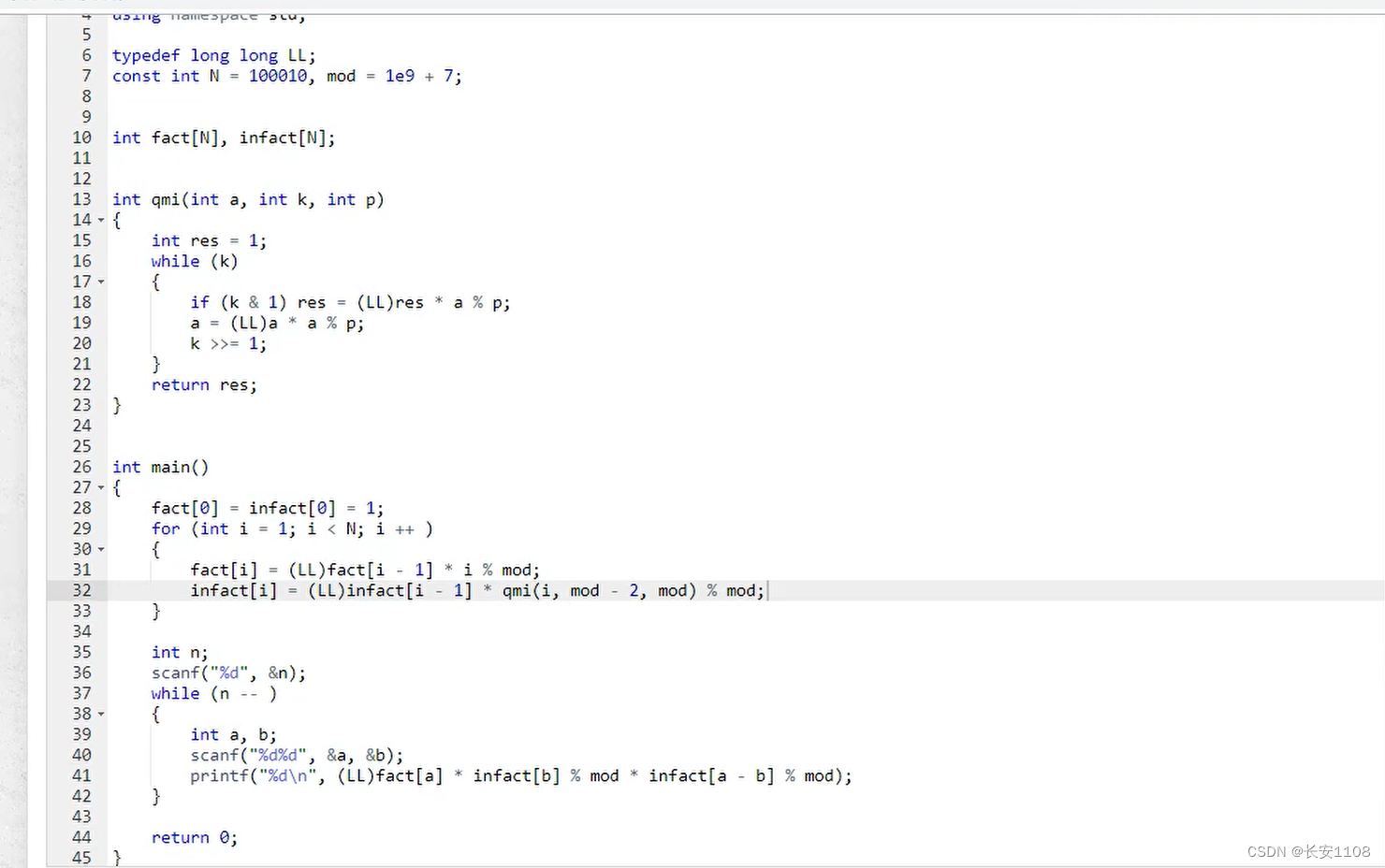
数据：N是a和b的数据范围，fact用来存储每个数的阶乘，infact用来存储每个数阶乘的逆元（或者可以理解为每个逆元的阶乘）

在mian函数中，进行预处理
首先对于0的阶乘以及阶乘的逆，都是1
之后，对于 i 从 1到N
fact[i] = (LL)fact[i-1] * i % mod;（因为fact[i-1] * i的范围超出了int的范围，所以将fact[i-1]转为LL之后，编译器会将后面的 i 也转为LL，这是编译器的隐式转换，此时结果是LL型的，之后%mod之后，数据范围可以被int类型的fact[i] 接收了）
infact[i] = (LL)infact[i-1] * qmi (i , mod -2,mod) % mod;
（对于这个qmi，就是在求 i 在模 mod 的情况下的逆元，因为mod是1e9+7是一个质数，所以可以用快速幂求逆元：i 的逆元就是 i 的 mod-2 次方 ，模 mod，带入到qmi函数中，就可以得到 i 在模 mod下的逆元 ，最后再模一个mod到int范围）

上面加一个快速幂的算法即可

组合数三（数据范围巨大，见下图）

算法思想

使用卢卡斯定理：

两者在mod p的情况下同余

例题+代码（求C时使用整理公式）

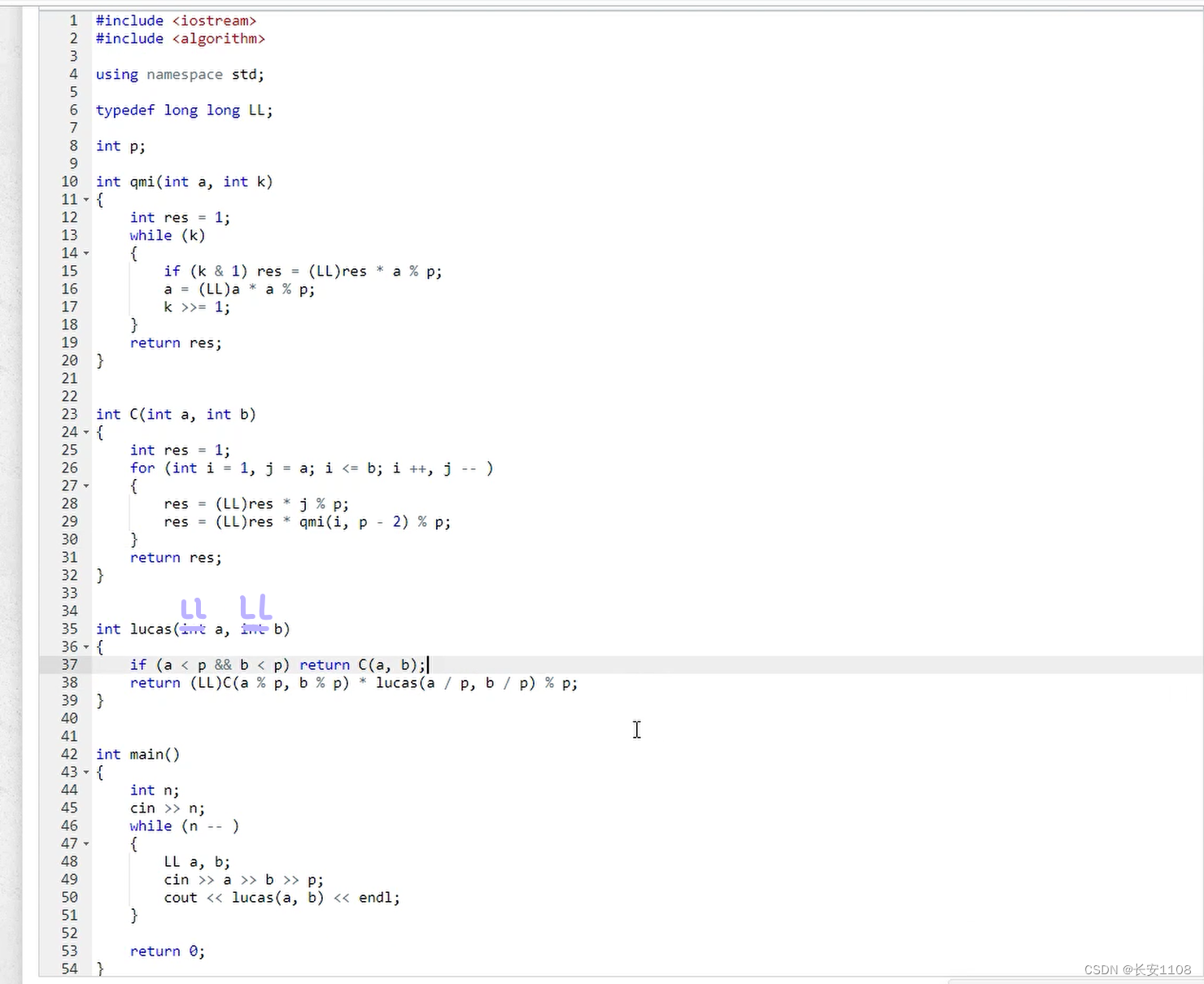
在最上面的全局位置，定义一个p，等待后续输入给p一个值
首先来说C函数
该函数就是计算Cab的组合数，从定义出发
首先res初始化为1，用于返回答案
之后for循环，i 从 1循环到小于等于b，i++；
所以代码中有res = res qmi（i ，p-2，p）% p，因为从组合数的计算来看，例如C62，结果是65/2！，分母是2！，所以 i 从1到等于b，i++，计算出b阶乘的逆元乘到res中（只不过这里是将一个阶乘中所有的元素依次计算出来依次乘进去的），%p是为了到int的范围，同时也满足题意
又因为分子上是从6开始递减乘，乘b的个数，因为 j 初始化为a，j–，每次乘上 j ，乘b遍，满足分子
最后返回res就是Cab的组合数
之后看重点：lucas函数
传入参数时要用LL，因为范围超过了2e9
在函数内，判断如果a，b都小于p，那么直接返回C（a，b）
否则， 返回（LL）C(a%p,b%p) 乘 lucas（a/p，b/p）最后% p （因为a%p，b%p已经是最小值了，取模之后都是最简值，所以不需要参与递归，而a/p，b/p，值不确定，需要加入到递归，最终从上面那个if结束递归）

最后加上快速幂求逆元的算法即可

求组合数四（答案无需mod一个数，直接算出来）

计算时使用高精度大数计算

基本思想

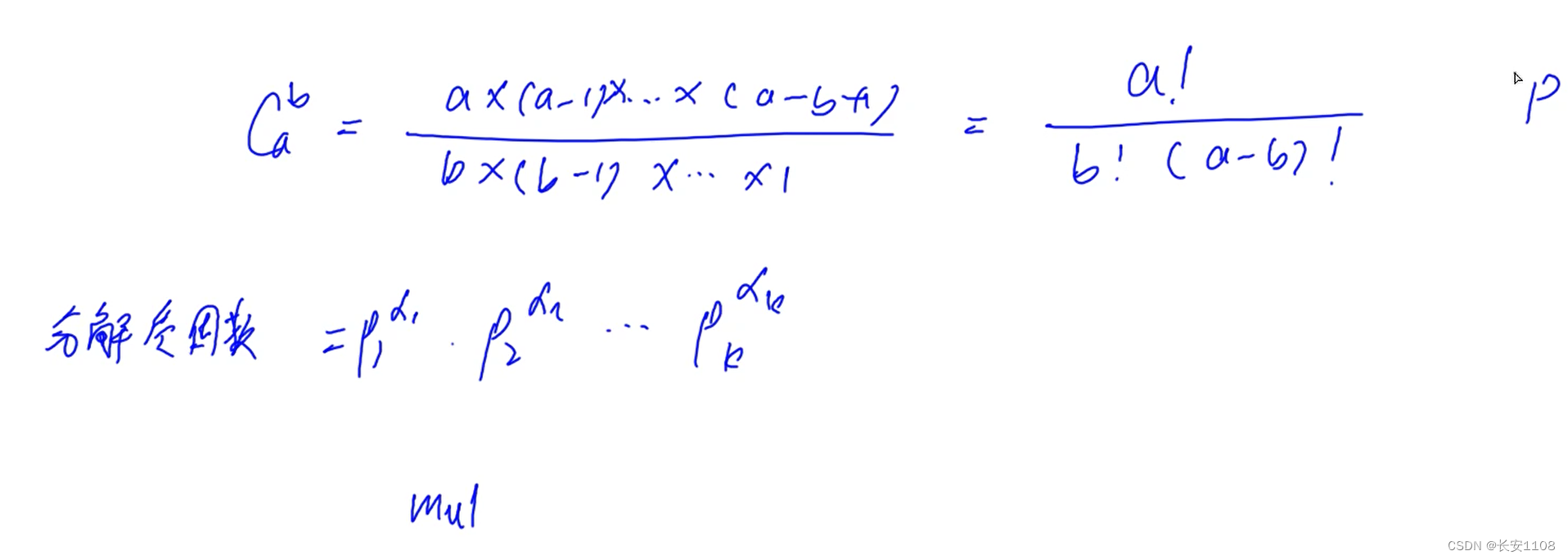
首先计算出Cab，因为这类题的结果往往很大，所以重点在于高精度的实现，
计算出Cab之后，第二步是将结果分解质因数，然后对其进行乘法的高精度运算即可
而我们无需直接计算出Cab的值，而是利用右边的阶乘公式，找到各个质因子p，找每个质因子的个数，分子上p的个数-分母上p的个数，就是质因子p的个数

而对于一个阶乘的某个质因子的个数，采用如下这种方式进行计算：

以a！为例，且以质因子之一的p为例，a！的p质子的个数是，a/p向下取整+a/p的平方向下取整+a/p的三次方向下取整…+加到p的某次方比a大为止
原理：a/p向下取整是计算出p的倍数的个数，然后，这里面可能有p的两倍的倍数但是被算了一个，实际上他可以被算两个p，所以，再加上“p的平方的倍数”的个数，但是这里面可能会有p的三次方被算了两个，实际上他可以被算作三个，所以再加上“p的三次方的倍数”的个数

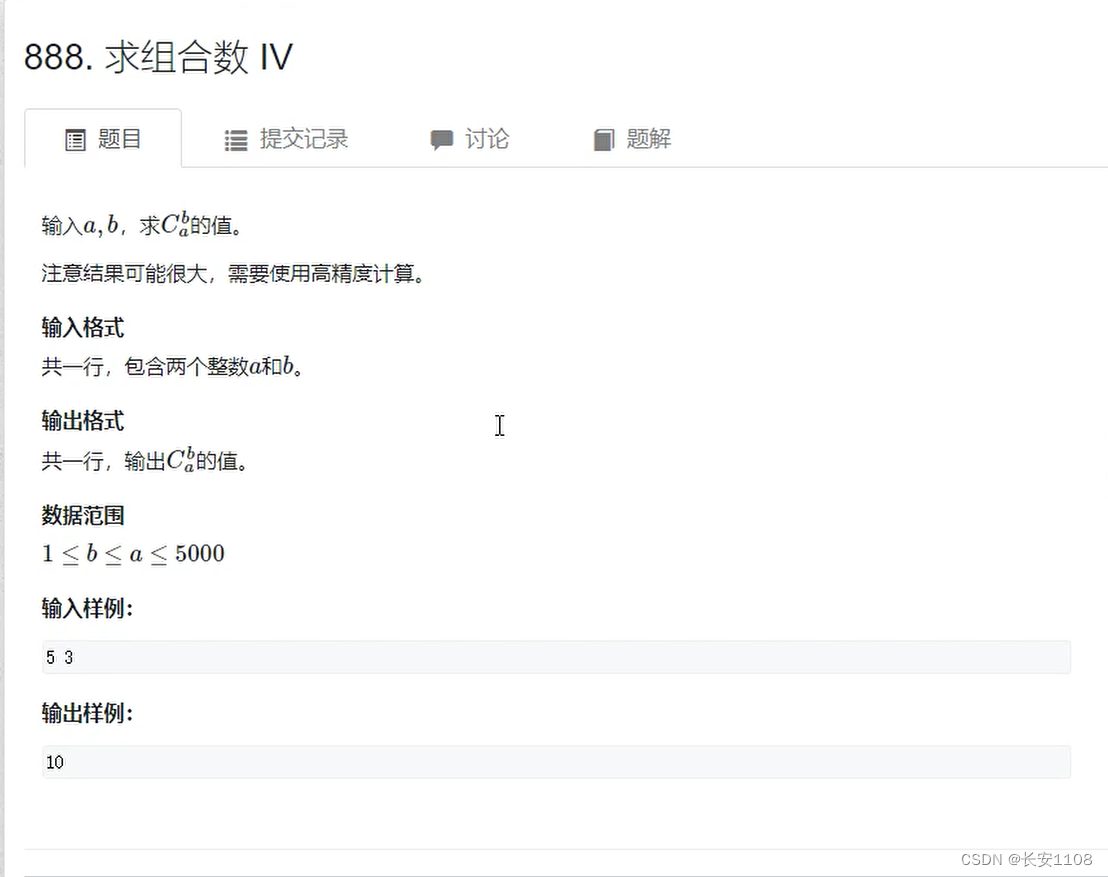
例题

真题感悟

遇到简单的组合数问题

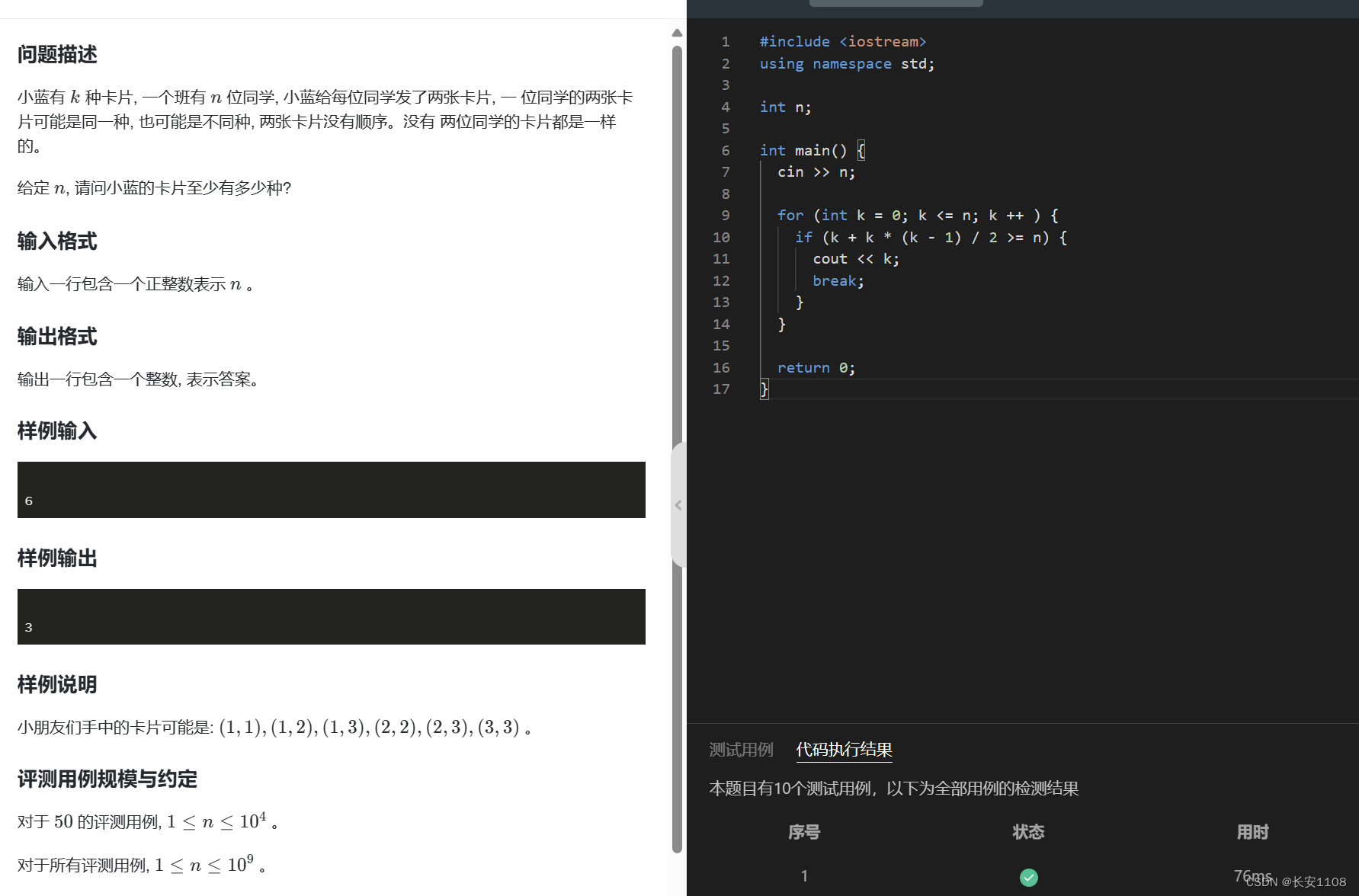
遇到如上图所示，cab中，已经给出了a或者b的值，且a或者b的值很小，那么可以直接把组合数的数学公式推出来，计算即可了，不用局限于写上模版，然后代数。

时间复杂度c++运行效率

对于c++来讲，如果将时间复杂度的n带入数据量，得到的数据在1e7到1e8次方，那么这样的时间复杂度可以在一秒内算出来

卡特兰数

简介+举例

卡特兰数定义：
给定n个0和n个1，对他们进行排序，排成2n的序列，如果排成的序列任意前缀序列中0的个数都要大于等于1的个数，那么这种序列就是卡特兰序列

求卡特兰序列的个数

算法基本思想

首先画出一个网格坐标表
然后，假如现在n为6，也就是有6个1和6个0
然后，我们规定0为向右走一格，1为向上走一格，因为我们有6个1和6个0，那么也就是有6个向上和6个向右，所以，我们最终的终点在（6，6），所以思路就转化为，从（0，0）走到（6，6），合法的路径有几条，
又因为卡特兰数规定，序列的任意前缀，0的个数都要大于等于1的个数，所以，对应到图上来说，就是路径不能越过从（0，0）到（6，6）的那条直线，或者说经过原点的斜率为1的线，但是可以与改线重合。换句话说，路径不能触碰到与该斜直线平行的上方的那条红线，所有触碰到那条线的路径都是不合法的，
所以，我们只需要计算出路线的总个数，减去不合法路线的个数，就可以得到合法路线的个数，就得到合法序列个数

总路线条数计算：C12、6，因为一共有12步，要选其中6步向上，其他都向右，顺序无所谓，所以是C12、6
而不合法路线条数计算：假如我们研究一条不合法路线，他会触碰到红线，将这个路线从“与红线重合的点”开始的后半段，关于红线对称过去，由于不合法路线最终的终点也是（6，6），所以，对称得到的路线的终点，永远是终点关于红点的对称点，此题为（5，7），所以，直接求从（0，0）到（5，7）的路线条数，就是其到（6，6）的不合法路线的条数，即C12、5
所以最终的合法的卡特兰数为C12、6-C12、5

转化到n就是：

C2n、n减去C2n、n-1
最终化简整理得:

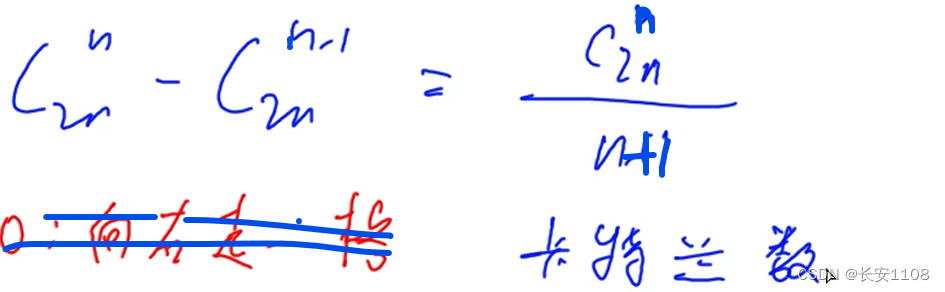
例题+代码（求C时使用整理公式）

这里就是按照算法思想来求，先求C2n、n，之后将得到的结果除以（n+1）
而求C2n、n的时候，因为题目要求取模，除法无法进行取模操作，所以求逆元，将除法转化为乘法之后，在计算的过程中时刻进行取模操作，避免越界，
而求逆元的方式有两个，选哪个取决于mod的数是否是质数，如果是质数，那么就用快速幂求逆元，如果不是质数，那么就用扩展欧几里得算法来求

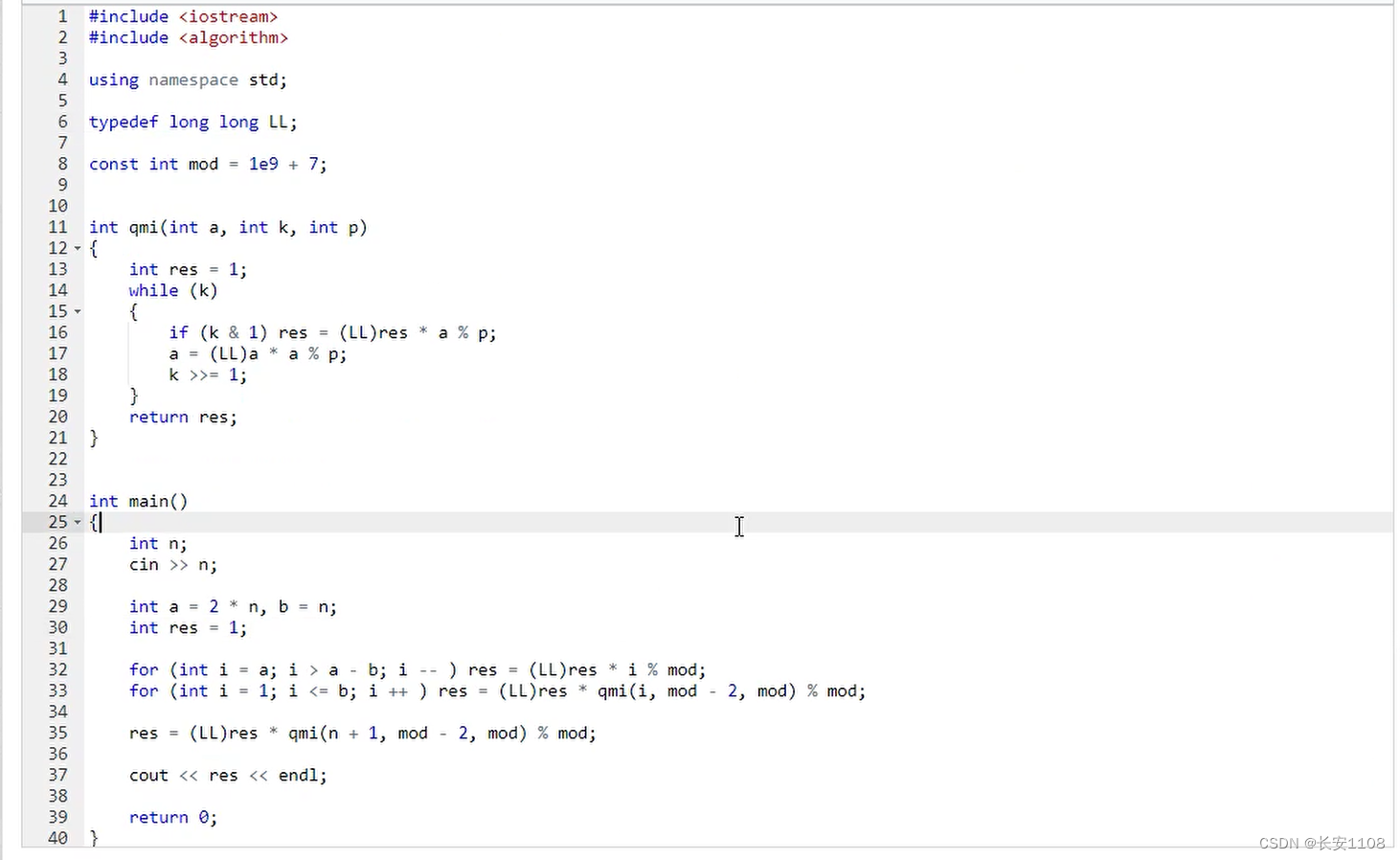
上图代码：
首先输入n，之后a=2n，b=n
之后初始化res = 1
然后两个for循环用来求C2n、n
第一个for循环用来求分子，从2n乘n个递减为1的数，i > a - b，通过举例归纳，合理，i – ，res = (LL)res * i % mod
第二个for循环用来求分母，即求b的阶乘，i从1到等于b，这时不是单独求分母，而是带着之前求出来的分子，对b！的每个数进行逆元乘积，所以是(LL)res * qmi(i, mod - 2, mod) % mod;
qmi，求 i 在模mod的情况下的转化成的逆元

最后的除以（n+1）也是使用逆元进行乘法之后取模