快速排序
快速排序是对冒泡排序的一种改进,它的基本思想是通过一趟排序将待排记录分割成独立的两部分,其中一部分的关键字比另一部分的关键字小,然后分别对这两部分进行快速排序,递归此过程,直到整个序列有序。
快速排序对包含n个数的输入数组,最坏情况运行时间较差,但是快速排序通常是用于排序的最佳的使用选择,它的平均性能相当好,期望为O(nlgn),隐含的常数因子很小。
就一趟排序而言,例如对数组a中的a[m..n]部分进行一趟快速排序,首先选择一个数组值,例如a[m]作为枢轴,然后1.从a[n]向左选择小于枢纽的数组值移动到a[m],2.从a[m+1]向右选择大于枢纽值移到步骤1移到左边的值的位置上,再从右边开始向左移动,重复1和2过程向中间靠拢,最后把枢纽值放在中间的某个位置上,完成一趟快速排序,代码如下:
//快速排序,对数组的a的low到high的元素a[low]-a[high]进行一次快速排序函数partition
int Partition(int a[],int low,int high)
{
//交换数组a[low..high]的记录,使a[low..high]范围内枢纽记录左边的值<=枢纽记录,右边的值>=枢纽记录
int pivotkey=a[low]; //用pivotkey暂存待排记录的第一个记录,作为枢轴记录
//从a[low..high]的两端向中间扫描,low和high作为数组下标,依次向中间靠拢,当low=high时,结束依次快速排序
while(low<high)
{
while(low<high && a[high]>=pivotkey) high--; //查找比pivotkey小的数组值a[high],然后存在a[low]上
a[low]=a[high];
while(low<high && a[low]<=pivotkey) low++; //查找比pivotkey大的数组值a[low],然后存在a[high]上
a[high]=a[low];
}//while
//将枢纽值存放在a[low]上,完成一次快速排序
a[low]=pivotkey;
//返回枢纽的位置,为了下次对左右两部分进行快速排序
return low;
}//Partition递归形式的快速排序算法代码如下:
//快速排序函数QuickSort
void QuickSort(int a[],int low,int high)
{
//对数组a[low..high]进行快速排序
if(low<high)
{
int av=Partition(a,low,high); //av值记录调用Parrtiton函数返回的枢纽值的数组下标,然后将a[low..high]分为两部分递归快速排序
QuickSort(a,low,av-1); //对a[low..av-1]进行快速排序
QuickSort(a,av+1,high); //对a[av+1..high]进行快速排序
}
}//QuickSort堆排序
堆排序属于选择排序,只需要一个记录大小的辅助空间,每个待排的记录仅占一个存储空间,运行时间复杂度为O(nlgn),是一种原地排序算法。
堆的定义如下,对于n个元素的序列{k1,k2,,kn},当满足k(i)<=k(2*i)且k(i)<=k(2*i+1)时称为小根堆,满足k(i)>=k(2*i)且k(i)>=k(2*i+1)时称为大根堆。如果将这个数组看成一个完全二叉树,则堆的含义表明,完全二叉树的所有非终端节点的值不大于(或者不小于)它的左、右孩子节点的值。如果上述数组是堆,则堆顶元素必为序列中n个元素的最小值(或者做大值)。
实现堆排序要解决两个问题:(1)如何由一个无序序列建成一个堆,(2)如何在输出堆顶元素后,调整剩余元素称为一个新的堆。
调整新堆思想(以大根堆为例):假设有一个二叉树对应的序列,根节点的左、右子树已经是大根堆,现在调整跟节点的值使调整后整个序列为一个大顶堆。令跟节点与孩子节点值较大的孩子节点比较,如果其值不小于孩子节点的值,则现在已经是大根堆;否则交换根节点和较大孩子节点的的位置,进行这一步后,新的根节点满足大根堆的定义,原来的根节点移到孩子节点的位置上,可能不满足大根堆的定义,此时以这个孩子节点作为新的根节点重复以上步骤。代码如下:
//堆排序,调整新堆函数HeapAdjust
void HeapAdjust(int a[],int s,int m)
{
//数组a[0]作为建堆过程的辅助空间,a[1..m]作为一个完全二叉树,此函数实现的功能是在a[s]的左右子树均为堆的条件下,
//建立a[s]以及其左右子树构成的完全二叉树也满足堆的定义
a[0]=a[s]; //辅助存储a[s]
for(int j=2*s;j<=m;j*=2)
{
if(j<m && a[j]<a[j+1]) j++; //选择左右孩子中较大的孩子
if(a[j]<=a[0]) //如果较大的孩子的值不大于它,则已经查到a[0]的位置
break;
a[s]=a[j]; //a[0]值较小,将孩子节点较大的存在a[s]上,并令s为此孩子节点
s=j;
}//for
a[s]=a[0]; //将a[0]即是原来的a[s]值放在查到到的适当的a[s]中,s可能已经改变
}//HeapAdjust堆排序:将堆顶元素(也就是序列的第一个)与未排序的最后一个元素交换位置(选择未排中最大的值排在后面),此时由于后面的值移到序列首位,执行HeapAdjust函数,调整新堆,反复此过程。
建堆、堆排序代码如下:
//堆排序实现函数HeapSort
void HeapSort(int a[],int m)
{
//对数组进行堆排序
for(int j=m/2;j>=1;j--) //从a[m/2]到a[1],构建堆
HeapAdjust(a,j,m);
//把堆顶值与j下标值交换,使最大的值依次排在数组后面,然后重新建堆
for(int j=m;j>1;--j)
{
a[0]=a[j];
a[j]=a[1];
a[1]=a[0];
HeapAdjust(a,1,j-1);
}//for
}//HeapSort归并排序
归并排序是将两个或者两个以上的有序表组合成一个新的有序表。它是一种稳定的排序方法,过程需要额外的空间,归并思想容易理解,一次归并过程代码如下:
//归并排序,将数组的相邻的两个有序序列归并为一个有序序列Merge函数
void Merge(int a[],int b[],int i,int m,int n)
{
//将有序的a[i..m]和有序的a[m+1..n]归并为有序的b[i..n]
int k=i,s=m+1;
//将a的两个有序序列归并为b的有序序列
for(;s<=n && i<=m;k++)
{
if(a[i]<=a[s]) b[k]=a[i++];
else b[k]=a[s++];
}//for
//当a的一个完全归并后,只需将另一个的剩余完全归并进b
if(s>n)
while(k<=n)
b[k++]=a[i++];
else
while(k<=n)
b[k++]=a[s++];
}//Merge
//递归实现的2-路归并函数MergeSort
void MergeSort(int a[],int b[],int s,int t)
{
//将a[s..t]归并为b[s..t]
if(s==t)
b[s]=a[s];
else
{
int c[N];
int m=(s+t)/2; //将a[s..t]平均分成a[s..m]和a[m+1..t]
MergeSort(a,c,s,m); //递归的将a[s..m]归并为c[s..m]
MergeSort(a,c,m+1,t); //递归的将a[m+1..t]归并为c[m+1..t]
Merge(c,b,s,m,t); //将c[s..m]和c[m+1..t]归并到b[s..t]
}//else
}//MergeSort各种排序方法的具体函数实现
#include <iostream>
using namespace std;
#define N 10 //定义待排数组的大小
//函数声明
void QuickSort(int a[],int low,int high);
void HeapSort(int a[],int m);
void MergeSort(int a[],int b[],int s,int t);
//main函数
int main(void)
{
int a[N]={15,3,9,26,11,7,18,33,21,6}; //快速排序
int a2[N+1]={0,15,3,9,26,11,7,18,33,21,6}; //堆排序
int a3[N]={15,3,9,26,11,7,18,33,21,6}; //归并排序
//对数组a进行快速排序输出排序结果
cout<<"快速排序结果如下:"<<endl;
QuickSort(a,0,9);
for(int i=0;i<N;i++)
cout<<a[i]<<" ";
cout<<endl<<endl;
//对数组a2进行堆排序输出排序结果
cout<<"堆排序结果如下:"<<endl;
HeapSort(a2,N);
for(int i=1;i<=N;i++)
cout<<a2[i]<<" ";
cout<<endl<<endl;
//对数组a3进行归并排序输出排序结果
cout<<"归并排序结果如下:"<<endl;
int a4[N]; //排序后
MergeSort(a3,a4,0,9);
for(int i=0;i<N;i++)
cout<<a4[i]<<" ";
cout<<endl<<endl;
system("pause");
return 0;
}
//*******************************************************
//快速排序,对数组的a的low到high的元素a[low]-a[high]进行一次快速排序函数partition
int Partition(int a[],int low,int high)
{
//交换数组a[low..high]的记录,使a[low..high]范围内枢纽记录左边的值<=枢纽记录,右边的值>=枢纽记录
int pivotkey=a[low]; //用pivotkey暂存待排记录的第一个记录,作为枢轴记录
//从a[low..high]的两端向中间扫描,low和high作为数组下标,依次向中间靠拢,当low=high时,结束依次快速排序
while(low<high)
{
while(low<high && a[high]>=pivotkey) high--; //查找比pivotkey小的数组值a[high],然后存在a[low]上
a[low]=a[high];
while(low<high && a[low]<=pivotkey) low++; //查找比pivotkey大的数组值a[low],然后存在a[high]上
a[high]=a[low];
}//while
//将枢纽值存放在a[low]上,完成一次快速排序
a[low]=pivotkey;
//返回枢纽的位置,为了下次对左右两部分进行快速排序
return low;
}//Partition
//快速排序函数QuickSort
void QuickSort(int a[],int low,int high)
{
//对数组a[low..high]进行快速排序
if(low<high)
{
int av=Partition(a,low,high); //av值记录调用Parrtiton函数返回的枢纽值的数组下标,然后将a[low..high]分为两部分递归快速排序
QuickSort(a,low,av-1); //对a[low..av-1]进行快速排序
QuickSort(a,av+1,high); //对a[av+1..high]进行快速排序
}
}//QuickSort
//***********************************************************
//堆排序,调整新堆函数HeapAdjust
void HeapAdjust(int a[],int s,int m)
{
//数组a[0]作为建堆过程的辅助空间,a[1..m]作为一个完全二叉树,此函数实现的功能是在a[s]的左右子树均为堆的条件下,
//建立a[s]以及其左右子树构成的完全二叉树也满足堆的定义
a[0]=a[s]; //辅助存储a[s]
for(int j=2*s;j<=m;j*=2)
{
if(j<m && a[j]<a[j+1]) j++; //选择左右孩子中较大的孩子
if(a[j]<=a[0]) //如果较大的孩子的值不大于它,则已经查到a[0]的位置
break;
a[s]=a[j]; //a[0]值较小,将孩子节点较大的存在a[s]上,并令s为此孩子节点
s=j;
}//for
a[s]=a[0]; //将a[0]即是原来的a[s]值放在查到到的适当的a[s]中,s可能已经改变
}//HeapAdjust
//堆排序实现函数HeapSort
void HeapSort(int a[],int m)
{
//对数组进行堆排序
for(int j=m/2;j>=1;j--) //从a[m/2]到a[1],构建堆
HeapAdjust(a,j,m);
//把堆顶值与j下标值交换,使最大的值依次排在数组后面,然后重新建堆
for(int j=m;j>1;--j)
{
a[0]=a[j];
a[j]=a[1];
a[1]=a[0];
HeapAdjust(a,1,j-1);
}//for
}//HeapSort
//*************************************************************************
//2-路归并排序,将数组的相邻的两个有序序列归并为一个有序序列Merge函数
void Merge(int a[],int b[],int i,int m,int n)
{
//将有序的a[i..m]和有序的a[m+1..n]归并为有序的b[i..n]
int k=i,s=m+1;
//将a的两个有序序列归并为b的有序序列
for(;s<=n && i<=m;k++)
{
if(a[i]<=a[s]) b[k]=a[i++];
else b[k]=a[s++];
}//for
//当a的一个完全归并后,只需将另一个的剩余完全归并进b
if(s>n)
while(k<=n)
b[k++]=a[i++];
else
while(k<=n)
b[k++]=a[s++];
}//Merge
//递归实现的2-路归并函数MergeSort
void MergeSort(int a[],int b[],int s,int t)
{
//将a[s..t]归并为b[s..t]
if(s==t)
b[s]=a[s];
else
{
int c[N];
int m=(s+t)/2; //将a[s..t]平均分成a[s..m]和a[m+1..t]
MergeSort(a,c,s,m); //递归的将a[s..m]归并为c[s..m]
MergeSort(a,c,m+1,t); //递归的将a[m+1..t]归并为c[m+1..t]
Merge(c,b,s,m,t); //将c[s..m]和c[m+1..t]归并到b[s..t]
}//else
}//MergeSort运行结果显示








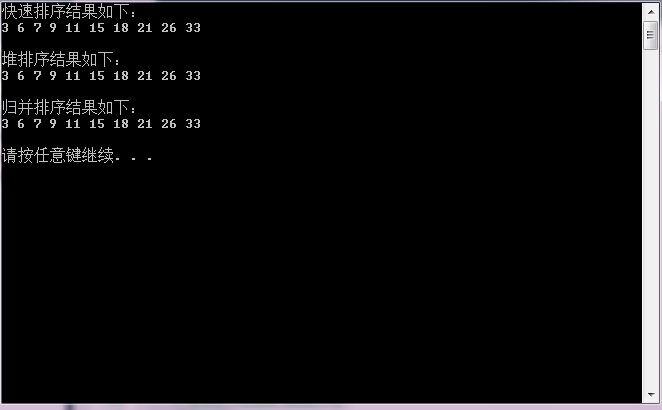














 3756
3756

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








