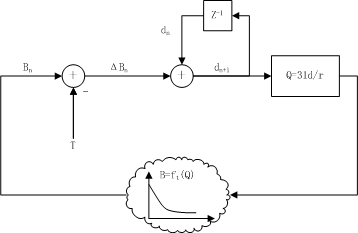
The core of TMN5 is the virtual buffer, the size of which is specified by r = alpha * bits_per_frame, where alpha is the multiple, typically 2. The larger value of alpha provides larger dynamical range, but less adjustment sensitivity. The current fullness of the buffer 'd' serves as the reference of quantization level 'Q', specifically, Q = 31 * d / r (31 is the maximal value for Q reached only when the buffer is full or overflown). The remaining available bits for coding within the GOP 'R' is calculated across the GOPs, say, 'R' for the current GOP no matter a surplus or a deficit, is carried over to the next GOP. This avoids the drifting caused by 'R' is restricted within GOP. In the case that B frames are absent, for I frame, the expected coding bits T = R * Xi / (Xi + Np * Xp); for P frame, T = R / Np, in which Xi and Xp are respectively current estimation of general complexity of I frames and P frames, Ni and Np number of the remaining corresponding frames. d = B - T, where B is the number of actual coded bits. 'd' is associated with R and separately counted for I and P frames, apparently it is a reasonable accumulative measurement of number of coded bits relative to due for either kind of frames. For given Q, the number of output bits can be denoted by B = f
t(Q). Obviously, f
t varies with frames (and therefore with time, that is why a 't' is put here), and is generally a decreasing function. According to the above discussion, the following equation set depicts the process:
ΔB n=B n-T
d n+1=d n+ΔB n
Q n=31*dn/r
B n=f t(Q n)
They can be simplified into:
Δd n=g t(d n)-T, where Δd n=ΔB n=d n+1-d n, g t(x)=f t(31*x/r)
Now we can see clearly that it represents a negative feedback loop.
If the differential |g t'(x)| keeps being less than 1, the system is stable and B wiggles around T (as both T and f are time varying).
ΔB n=B n-T
d n+1=d n+ΔB n
Q n=31*dn/r
B n=f t(Q n)
They can be simplified into:
Δd n=g t(d n)-T, where Δd n=ΔB n=d n+1-d n, g t(x)=f t(31*x/r)
Now we can see clearly that it represents a negative feedback loop.
If the differential |g t'(x)| keeps being less than 1, the system is stable and B wiggles around T (as both T and f are time varying).























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








