此文章可以使用目录功能哟↑(点击上方[+])
 Lonlife-ACM 1000 - Spoon Devil's 3-D Matrix
Lonlife-ACM 1000 - Spoon Devil's 3-D Matrix
Accept: 0 Submit: 0
Time Limit: 1s Memory Limit : 32MByte
 Problem Description
Problem Description
Spoon Devil build a 3-D matrix, and he(or she) wants to know if he builds some bases what's the shortest distance to connect all of them.
 Input
Input
There are multiple test cases. The first line of input contains an integer T, indicating the number of test cases. For each test case:
The first line contains one integer n(0<n<50), indicating the number of all points. Then the next n lines, each lines contains three numbers xi,yi,zi indicating the position of i-th point.
 Output
Output
For each test case, output a line, which should accurately rounded to two decimals.
 Sample Input
Sample Input
2
1 1 0
2 2 0
3
1 2 3
0 0 0
1 1 1
 Sample Output
Sample Output
3.97
 Hint
Hint
 Problem Idea
Problem Idea
解题思路:
【题意】
在三维坐标中有n个点
问连接这n个点的最短距离为多少
【类型】
最小生成树
【分析】
显然这是一道最小生成树的题目,如果你知道最小生成树的话
对于最小生成树的题目,存在两种常用解法:prim和kruskal
这两种算法分别是这样描述的
prim:任选一个结点放入点集S中,一般选取结点1,即S={1},每次挑选与点集S直接相邻的边权最小的且不属于点集S的结点加入点集S中,直到所有的点都加入点集S内。
举例:
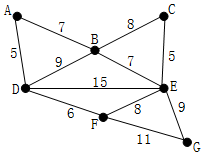
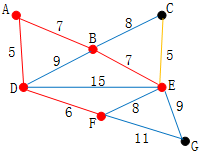
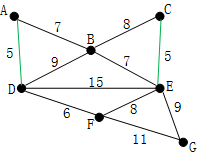
上图为原始的加权连通图,每条边一侧的数字代表其权值
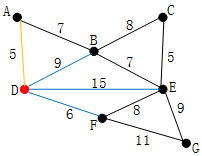
任选一点作为起始点(例如结点D),顶点A、B、E和F通过单条边与D相连,A是距离D最近的顶点,因此将A加入到点集S中,此时最短距离为5
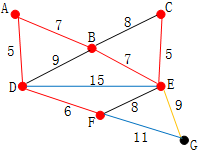
下一个顶点为距离D或A最近的顶点。B距D为9,距A为7,E为15,F为6。因此,F距D或A最近,因此将顶点F加入到点集S中,此时最短距离为5+6=11
算法继续重复上面的步骤。距离A为7的顶点B加入到点集S中,此时最短距离为11+7=18
在当前情况下,可以在C、E与G间进行选择。C距B为8,E距B为7,G距F为11。点E最近,因此将顶点E加入点集S中,此时最短距离为18+7=25
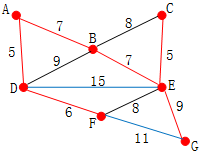
这里,可供选择的顶点只有C和G。C距E为5,G距E为9,故选取C加入点集S中,此时最短距离为25+5=30
顶点G是唯一剩下的顶点,它距F为11,距E为9,E最近,故将最后的点G加入点集S中,此时最短距离为30+9=39
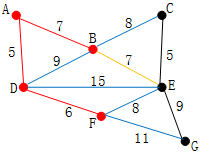
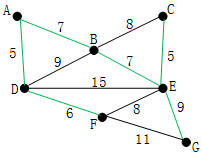
现在,所有顶点均已被选取,图中红色部分即为连通图的最小生成树。在此例中,最小生成树的权值之和为39。
kruskal:每次选取未在边集E中的最短边加入边集E中,若选取的边使得边集内的图存在回路,则丢弃该边,直到每个点都在边集内
举例:
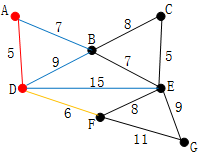
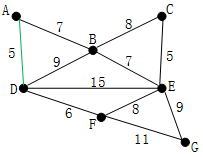
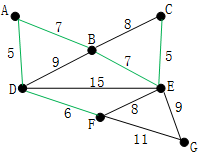
将边从小到大排序之后,我们率先选择了边AD,此时最短距离为5
第二步,在剩下的边中寻找。我们找到了CE。这里边的权重也是5,此时最短距离为5+5=10
依次类推我们找到了6,7,7。完成之后,图变成了这个样子,此时最短距离为5+5+6+7+7=30
这一步就是关键了。下面选择那条边呢? BC或者EF吗?都不是,尽管现在长度为8的边是最小的未选择的边。但是他们已经连通了(对于BC可以通过CE,EB来连接,类似的EF可以通过EB,BA,AD,DF来接连)。所以我们不需要选择他们。类似的BD也已经连通了。
最后就剩下EG和FG了。当然我们选择了EG。最后成功的图就是上图,最短距离为5+5+6+7+7+9=39
两种方法均已经介绍完毕,prim配合着邻接表或邻接矩阵,会有两种不同的时间复杂度做法
博主会给出三种做法的AC代码,读者可自行比较。
【时间复杂度&&优化】
kruskal:O(ElogE) prim+邻接矩阵:O(V*V) prim+邻接表:O(ElogV)
题目链接→Lonlife-ACM 1000 - Spoon Devil's 3-D Matrix
 Source Code
Source Code
/*Sherlock and Watson and Adler*/
//Prim + 邻接表
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 55;
const int M = 100005;
const int inf = 1000000007;
const int mod = 1000000007;
struct node
{
double x,y,z;
}s[N];
struct edge
{
int v,to;
double d;
bool operator < (const edge &a) const
{
return d>a.d;//最小值优先
}
}e[N*N];
int h[N],p;
bool v[N];
void add_edge(int u,int v,double d)
{
e[p].v=v;
e[p].d=d;
e[p].to=h[u];
h[u]=p++;
e[p].v=u;
e[p].d=d;
e[p].to=h[v];
h[v]=p++;
}
double distant(node a,node b)
{
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)+(a.z-b.z)*(a.z-b.z));
}
int main()
{
int t,n,i,j,k;
double ans;
edge u;
priority_queue<edge> q;
scanf("%d",&t);
while(t--)
{
p=0;ans=0;
while(!q.empty())
q.pop();
memset(h,-1,sizeof(h));
memset(v,false,sizeof(v));
scanf("%d",&n);
for(i=1;i<=n;i++)
scanf("%lf%lf%lf",&s[i].x,&s[i].y,&s[i].z);
for(i=1;i<=n;i++)
for(j=i+1;j<=n;j++)
add_edge(i,j,distant(s[i],s[j]));
v[1]=true;k=1;
for(i=h[1];i+1;i=e[i].to)
if(!v[e[i].v])
q.push(e[i]);
while(k!=n)
{
u=q.top();
q.pop();
if(v[u.v])
continue;
v[u.v]=true;
k++;
ans+=u.d;
for(i=h[u.v];i+1;i=e[i].to)
if(!v[e[i].v])
q.push(e[i]);
}
printf("%.2f\n",ans);
}
return 0;
}/*Sherlock and Watson and Adler*/
//Prim + 邻接矩阵
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 55;
const int M = 100005;
const int inf = 1000000007;
const int mod = 1000000007;
struct node
{
double x,y,z;
}s[N];
struct edge
{
int v;
double d;
edge(){}
edge(int _v,double _d):v(_v),d(_d){}
bool operator < (const edge &a) const
{
return d>a.d;//最小值优先
}
};
double g[N][N];
bool v[N];
double distant(node a,node b)
{
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)+(a.z-b.z)*(a.z-b.z));
}
int main()
{
int t,n,i,j,k;
double ans;
edge u;
priority_queue<edge> q;
scanf("%d",&t);
while(t--)
{
ans=0;
while(!q.empty())
q.pop();
memset(v,false,sizeof(v));
scanf("%d",&n);
for(i=1;i<=n;i++)
scanf("%lf%lf%lf",&s[i].x,&s[i].y,&s[i].z);
for(i=1;i<=n;i++)
for(j=i+1;j<=n;j++)
g[i][j]=g[j][i]=distant(s[i],s[j]);
v[1]=true;k=1;
for(i=1;i<=n;i++)
if(!v[i])
q.push(edge(i,g[1][i]));
while(k!=n)
{
u=q.top();
q.pop();
if(v[u.v])
continue;
v[u.v]=true;
k++;
ans+=u.d;
for(i=1;i<=n;i++)
if(!v[i])
q.push(edge(i,g[u.v][i]));
}
printf("%.2f\n",ans);
}
return 0;
}/*Sherlock and Watson and Adler*/
//Kruskal
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 55;
const int M = 100005;
const int inf = 1000000007;
const int mod = 1000000007;
struct node
{
double x,y,z;
}s[N];
struct edge
{
int u,v;
double d;
}e[N*N/2];
bool cmp(edge x,edge y)
{
return x.d<y.d;
}
int c[N];
int fun(int x)
{
if(c[x]!=x)
c[x]=fun(c[x]);
return c[x];
}
double distant(node a,node b)
{
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)+(a.z-b.z)*(a.z-b.z));
}
int main()
{
int t,n,i,j,p;
double ans;
scanf("%d",&t);
while(t--)
{
ans=0;p=0;
scanf("%d",&n);
for(i=1;i<=n;i++)
{
scanf("%lf%lf%lf",&s[i].x,&s[i].y,&s[i].z);
c[i]=i;
}
for(i=1;i<=n;i++)
for(j=i+1;j<=n;j++)
{
e[p].u=i;e[p].v=j;
e[p++].d=distant(s[i],s[j]);
}
sort(e,e+p,cmp);
for(i=0;i<p;i++)
{
if(fun(e[i].u)==fun(e[i].v))
continue;
c[fun(e[i].u)]=fun(e[i].v);
ans+=e[i].d;
}
printf("%.2f\n",ans);
}
return 0;
}

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








