此文章可以使用目录功能哟↑(点击上方[+])
集训队呆了那么长时间,还是只会划划水...
 Problem 1002 Fraction
Problem 1002 Fraction
Accept: 0 Submit: 0
Time Limit: 2000/1000 MS (Java/Others) Memory Limit : 65536/65536 K (Java/Others)
 Problem Description
Problem Description
Mr. Frog recently studied how to add two fractions up, and he came up with an evil idea to trouble you by asking you to calculate the result of the formula below:
As a talent, can you figure out the answer correctly?
 Input
Input
The first line contains only one integer T, which indicates the number of test cases.
For each test case, the first line contains only one integer n (n≤8).
The second line contains n integers: a1,a2,⋯an(1≤ai≤10).
The third line contains n integers: b1,b2,⋯,bn(1≤bi≤10).
 Output
Output
For each case, print a line “Case #x: p q”, where x is the case number (starting from 1) and p/q indicates the answer.
You should promise that p/q is irreducible.
 Sample Input
Sample Input
2
1 1
2 3
 Sample Output
Sample Output
Hint
Here are the details for the first sample:
2/(1+3/1) = 1/2
 Problem Idea
Problem Idea
解题思路:
【题意】
给你一个整数n
以及数组a1,a2,…,an
数组b1,b2,…,bn
要求求出
【类型】
签到模拟题
【分析】
题目还是比较好理解的,就是求下面这个东西
因为n最大才8,所以毫无疑问暴力的做法是最佳选择
因此,我们只需从公式内部往外计算就可以了
另外由于最终答案会以分数形式输出,所以过程中两数还不能直接相除,分子和分母要分开计算
最初,分子x(0)为bn,分母y(0)为an
一轮计算后,分子x(1)为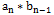
显然,k轮计算后,分子x(k)为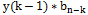
都是和前一轮结果相关的
所以还是靠循环搞定
【时间复杂度&&优化】
O(n)
题目链接→HDU 5912 Fraction
 Source Code
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 10;
const int M = 100005;
const int inf = 1000000007;
const int mod = 101;
int a[N],b[N];
int gcd(int a,int b)
{
if(a%b)
return gcd(b,a%b);
return b;
}
int main()
{
int t,n,i,x,y,z,k,p=1;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
for(i=1;i<=n;i++)
scanf("%d",&a[i]);
for(i=1;i<=n;i++)
scanf("%d",&b[i]);
y=a[n];x=b[n];
for(i=n-1;i>0;i--)
{
z=y;
y=y*a[i]+x;
x=z*b[i];
}
k=gcd(x,y);
printf("Case #%d: %d %d\n",p++,x/k,y/k);
}
return 0;
}  Problem 1004 Triangle
Problem 1004 Triangle
Accept: 0 Submit: 0
Time Limit: 2000/1000 MS (Java/Others) Memory Limit : 65536/65536 K (Java/Others)
 Problem Description
Problem Description
Mr. Frog has n sticks, whose lengths are 1,2, 3⋯n respectively. Wallice is a bad man, so he does not want Mr. Frog to form a triangle with three of the sticks here. He decides to steal some sticks! Output the minimal number of sticks he should steal so that Mr. Frog cannot form a triangle with
any three of the remaining sticks.
 Input
Input
The first line contains only one integer T (T≤20), which indicates the number of test cases.
For each test case, there is only one line describing the given integer n (1≤n≤20).
 Output
Output
For each test case, output one line “Case #x: y”, where x is the case number (starting from 1), y is the minimal number of sticks Wallice should steal.
 Sample Input
Sample Input
4
5
6
 Sample Output
Sample Output
Case #2: 1
Case #3: 2
 Problem Idea
Problem Idea
解题思路:
【题意】
长度为1,2,3,…,n的n根木棒
问至少偷走几根木棒,才能使得剩下的木棒任意三根都无法组成三角形
【类型】
打表
【分析】
我们都知道,三根木棒要构成三角形
需满足三根木棒中任意两根木棒长度之和大于剩下的那根木棒
对于1,2,3,…,n这n根木棒,为了尽可能构不成三角形
显然尽可能要留下长度小的
为什么呢?
假设三根木棒中较短的两根木棒长度分别为x,y,且y>x
那么,最长的那根木棒长度只要<x+y(当然,长度肯定是>y的)就可以构成三角形
那么,x和y的值越大,意味着最长的那根木棒可选择性越大
这就需要去掉更多的木棒才能使得剩下的模板构不成三角形
故需要尽可能留下长度小的木棒
因此,对于1,2,3,…,20这些长度的木棒,显然要留下的木棒为1,2,3,5,8,13(斐波那契数列有木有^_^)
于是,照此打表输出即可
【时间复杂度&&优化】
O(1)
题目链接→HDU 5914 Triangle
 Source Code
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 25;
const int M = 100005;
const int inf = 1000000007;
const int mod = 101;
int s[N]={0,0,0,0,1,1,2,3,3,4,5,6,7,7,8,9,10,11,12,13,14};
int main()
{
int t,n,i,p=1;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
printf("Case #%d: %d\n",p++,s[n]);
}
return 0;
}  Problem 1006 Harmonic Value Description
Problem 1006 Harmonic Value Description
Accept: 0 Submit: 0
Time Limit: 2000/1000 MS (Java/Others) Memory Limit : 65536/65536 K (Java/Others)
Special Judge
 Problem Description
Problem Description
The harmonic value of the permutation p1,p2,⋯pn is
Mr. Frog is wondering about the permutation whose harmonic value is the strictly k-th smallest among all the permutations of [n].
 Input
Input
The first line contains only one integer T (1≤T≤100), which indicates the number of test cases.
For each test case, there is only one line describing the given integers n and k (1≤2k≤n≤10000).
 Output
Output
For each test case, output one line “Case #x: p1 p2 ⋯ pn”, where x is the case number (starting from 1) and p1 p2 ⋯ pn is the answer.
 Sample Input
Sample Input
4 1
4 2
 Sample Output
Sample Output
Case #2: 2 4 1 3
 Problem Idea
Problem Idea
解题思路:
【题意】
1~n的全排列中谐波值严格第k小的排列为多少
排列p1,p2,…,pn的谐波值定义如下:
【类型】
构造
【分析】
此题关键是找突破口
在没找到突破口前强行做还是有点难度的
由于p1,p2,…,pn是1~n全排列中的一种
可想而知的是,严格第1小的排列必定是那种任意相邻两个数最大公约数为1的排列,例如排列1,2,3,…,n
此外,1~n这n个数还是很奇妙的,我们可以构造出任意约数为k的对,当然,前提是k<=n/2
故严格第k小的排列可以是存在一对相邻两个数最大公约数为k,其余任意相邻两个数最大公约数为1的排列
另外,题目已经做了方便我们构造的规定
即2k≤n
故最方便的构造方法是将2k和k提取出来放在排列最前面,然后构造相邻两数最大公约数为1的排列
即下述这种排列:
2k,k,k-1,k-2,…,2,1,k+1,k+2,…,2k-1,2k+1,…,n-1,n
这么做的原因如下:
⑴gcd(k,2k)=k
⑵自然数中相邻两数的最大公约数为1
⑶自然数中相邻两奇数的最大公约数为1,即gcd(2k-1,2k+1)=1
⑷1与任何数的最大公约数为1
【时间复杂度&&优化】
O(n)
题目链接→HDU 5916 Harmonic Value Description
 Source Code
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 25;
const int M = 100005;
const int inf = 1000000007;
const int mod = 101;
int main()
{
int t,n,k,i,p=1;
scanf("%d",&t);
while(t--)
{
scanf("%d%d",&n,&k);
printf("Case #%d:",p++);
printf(" %d %d",2*k,k);
for(i=k-1;i>=1;i--)
printf(" %d",i);
for(i=k+1;i<=n;i++)
if(i!=2*k)
printf(" %d",i);
puts("");
}
return 0;
}  Problem 1008 Sequence I
Problem 1008 Sequence I
Accept: 0 Submit: 0
Time Limit: 3000/1500 MS (Java/Others) Memory Limit : 65536/65536 K (Java/Others)
 Problem Description
Problem Description
Mr. Frog has two sequences a1,a2,⋯,an and b1,b2,⋯,bm and a number p. He wants to know the number of positions q such that sequence b1,b2,⋯,bm is exactly the sequence 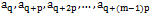
 Input
Input
The first line contains only one integer T≤100, which indicates the number of test cases.
Each test case contains three lines.
The first line contains three space-separated integers 1≤n≤10^6,1≤m≤10^6 and 1≤p≤10^6.
The second line contains n integers a1,a2,⋯,an(1≤ai≤10^9).
the third line contains m integers b1,b2,⋯,bm(1≤bi≤10^9).
 Output
Output
For each test case, output one line “Case #x: y”, where x is the case number (starting from 1) and y is the number of valid q’s.
 Sample Input
Sample Input
6 3 1
1 2 3 1 2 3
1 2 3
6 3 2
1 3 2 2 3 1
1 2 3
 Sample Output
Sample Output
Case #2: 1
 Problem Idea
Problem Idea
解题思路:
【题意】
已知序列A和序列B以及p
问有多少个位置q,使得b1,b2,…,bm与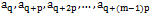
【类型】
KMP
【分析】
其实本题只是在裸的KMP上做了稍微的修改罢了
裸的KMP是一一匹配,而本题要求的是隔p个匹配
因此,计算next数组部分是不需要修改的,只需要改一下匹配过程
当序列A中的a[i]等于序列B中的b[j]时,将原先的i++改为i+=p即可
【时间复杂度&&优化】
O(N+M)
题目链接→HDU 5918 Sequence I
 Source Code
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 1000005;
const int M = 100005;
const int inf = 1000000007;
const int mod = 101;
int c[N],s[N],s2[N],n,m,p;
void getnext()
{
int i=0,j=-1,l=m;
c[0]=-1;
while(i<l)
if(j==-1||s2[i]==s2[j])
c[++i]=++j;
else
j=c[j];
}
int kmp(int x)
{
int i=x,j=0,k=0,len=n,l=m;
while(i<len)
{
if(j==-1|s[i]==s2[j])
i+=p,j++;
else
j=c[j];
if(j==l)
k++,j=c[j];
}
return k;
}
int main()
{
int t,i,ans,k=1;
scanf("%d",&t);
while(t--)
{
ans=0;
scanf("%d%d%d",&n,&m,&p);
for(i=0;i<n;i++)
scanf("%d",&s[i]);
for(i=0;i<m;i++)
scanf("%d",&s2[i]);
getnext();
for(i=0;i<p&&i<n;i++)
ans+=kmp(i);
printf("Case #%d: %d\n",k++,ans);
}
return 0;
}  Problem 1010 Ugly Problem
Problem 1010 Ugly Problem
Accept: 0 Submit: 0
Time Limit: 2000/1000 MS (Java/Others) Memory Limit : 65536/65536 K (Java/Others)
Special Judge
 Problem Description
Problem Description
Everyone hates ugly problems.
You are given a positive integer. You must represent that number by sum of palindromic numbers.
A palindromic number is a positive integer such that if you write out that integer as a string in decimal without leading zeros, the string is an palindrome. For example, 1 is a palindromic number and 10 is not.
 Input
Input
In the first line of input, there is an integer T denoting the number of test cases.
For each test case, there is only one line describing the given integer s (1≤s≤10^1000).
 Output
Output
For each test case, output “Case #x:” on the first line where x is the number of that test case starting from 1. Then output the number of palindromic numbers you used, n, on one line. n must be no more than 50. en output n lines, each containing one of your palindromic numbers. Their sum must be exactly s.
 Sample Input
Sample Input
18
1000000000000
 Sample Output
Sample Output
2
9
9
Case #2:
2
999999999999
1
Hint
9 + 9 = 18
999999999999 + 1 = 1000000000000
 Problem Idea
Problem Idea
解题思路:
【题意】
给你一个整数s,要求将它拆分成不超过50个回文整数相加
输出这些回文整数
回文整数的定义为该整数存储成字符串时,是回文串
【类型】
大数+模拟
【分析】
每次将当前结果的前半段取出来,-1,构造成回文串y,x-=y,直到x=0
特殊处理0~20的情况
具体看代码,不懂提问
【时间复杂度&&优化】
O(n)
 Source Code
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<bitset>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-9
#define LL long long
#define PI acos(-1.0)
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 1005;
const int M = 55;
const int inf = 1000000007;
const int mod = 101;
char s[N];
int x[N],y[N],ans[M][N],u[2]={1,1};
void sub(int *a,int *b)//大数减法
{
int i;
for(i=1;i<=b[0];i++)
a[i]-=b[i];
for(i=1;i<=a[0];i++)
if(a[i]<0)
a[i]+=10,a[i+1]--;
while(a[0]>1&&!a[a[0]])
a[0]--;
}
int main()
{
int t,i,j,n,k,p=1;
scanf("%d",&t);
while(t--)
{
k=0;
scanf("%s",s);
n=strlen(s);
x[0]=n;//记录当前位数
for(i=0;s[i]!='\0';i++)
x[n-i]=s[i]-'0';
while(!(x[0]==1&&x[1]==0))
{
if(x[0]==1)//当前为一位数
{
ans[k][0]=1;
ans[k++][1]=x[1];
break;
}
if(x[0]==2&&x[2]==1)//当前为十位为1的两位数
{
if(x[1]==0)//10
{
ans[k][0]=1;
ans[k++][1]=9;//9
ans[k][0]=1;//+
ans[k++][1]=1;//1
break;
}
if(x[1]==1)//11
{
ans[k][0]=2;
ans[k][1]=1;
ans[k++][2]=1;//11
break;
}
ans[k][0]=2;
ans[k][1]=1;
ans[k++][2]=1;//11
ans[k][0]=1;
ans[k++][1]=x[1]-1;
break;
}
for(i=x[0];i>x[0]/2;i--)
y[i-x[0]/2]=x[i];
y[0]=(x[0]+1)/2;//取出当前数的前一半
sub(y,u);
ans[k][0]=y[0]+y[0];
if(ans[k][0]>x[0])
ans[k][0]--;
for(i=y[0],j=0;i;i--,j++)
ans[k][ans[k][0]-j]=ans[k][y[0]-i+1]=y[i];//构造回文串
sub(x,ans[k++]);
}
printf("Case #%d:\n%d\n",p++,k);
for(i=0;i<k;i++)
{
for(j=ans[i][0];j;j--)
printf("%d",ans[i][j]);
puts("");
}
}
return 0;
}










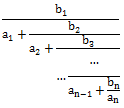
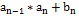
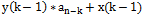
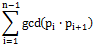














 1382
1382

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








