使用二分法与牛顿迭代实现sqrt(int)

二分法实现sqrt(int)
使用二分法逼近求解sqrt(x)
x的根不大于x/2+1,只需在[0,X/2+1]内二分查找即可
证明：
假设 sqrt(x)<=x/2+1
则有 => x<= (x/2+1)^2 => x<=x^2/4+1+x => x^2/4+1 =>0
而 x^2/4+1 =>0恒成立。
由于实现的代码返回值 即x的根为int 型的，舍去了小数部分

int mySqrt(int x) {
        long long left=0;
        long long right=x/2+1;
        while(left<=right)
        {
            long long mid=(left+right)>>1;
            long long sq=mid*mid;
            if(sq==x) return mid;
            else if(sq<x)left=mid+1;
            else right=mid-1;
        }
        return right;
    }

牛顿迭代实现sqrt(int)
牛顿法（英语：Newton’s method）又称为牛顿-拉弗森方法（英语：Newton-Raphson method），它是一种在实数域和复数域上近似求解方程的方法。方法使用函数 f(x)的泰勒级数的前面几项来寻找方程 f(y)=0的根。

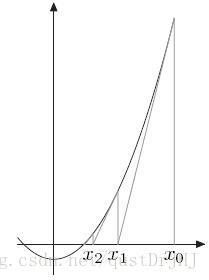
首先，选择一个接近函数f(x)零点的 x0，计算相应的 f(x0)和切线斜率 f’(x0)（这里 f’表示函数 f的导数）。然后我们计算穿过点 (x0,f(x0)并且斜率为 f’(x0)的直线和 x轴的交点的 x坐标，也就是求如下方程的解：
0=(x-x0)f’(x0})+f(x0)
我们将新求得的点的x坐标命名为x_1，通常 x_1会比 x0更接近方程 f(x)=0的解。因此我们现在可以利用 x_1开始下一轮迭代。迭代公式可化简为如下所示：
Xn+1=Xn - f(Xn)/f’(Xn)
如果 f’是连续的，并且待求的零点 x是孤立的，那么在零点 x周围存在一个区域，只要初始值x_{0}位于这个邻近区域内，那么牛顿法必定收敛。
并且，如果 f’(x)!=0，那么牛顿法将具有平方收敛的性能。粗略的说，这意味着每迭代一次，牛顿法结果的有效数字将增加一倍。

sqrt(int)的实现：
x^2=r => f(x)=x^2-r 当f(x)=0时的解，设(Xi,Xi^2-r)为f(x)上的一点，过该点的切线
方程为 f(x)-f(Xi)=f’(Xi)*(x-Xi),令切线方程等于0，即可求得x=x-f(Xi)/f’(Xi)
=> x=x-(Xi^2-r)/(2*Xi)=(Xi+r/Xi)/2
通过每次判断前后两次迭代出的结果是否相等来结束迭代

牛顿迭代中的重点之重在于初始点的选取，尽量选取靠近f(x)=0的x点，这样会节省计算次数。

int mySqrt2(int x){
        long r=x/2+1;
        while(r*r > x)
        {
            r=(r+x/r)>>1;
        }
        return r;
    }