二分查找的尾递归和循环形式的分析

1.概念：建立在有序集合上分段的进行查找。在生活中，假如你们在玩一个扑克，你的同伴随便拿了一张牌让你来猜大小，同时他会告诉你你的猜测是偏大还是偏小，那你应该怎么猜可以最快的猜出答案呢？答案就是二分查找：每次都猜中间的数，将猜测的范围减半。

2.实现：首先看二分查找的递归形式，因为它易于理解

	//尾递归形式,num为待查数
	public static int rank1(int num, int lo, int hi){
		if(hi < lo) return lo;
		int mid = lo + (hi - lo) / 2;		//注意这个的mid求法没有写成mid = (lo + hi) / 2 的形式可以加快运行速度（大数的除法会耗时久），并且放置溢出（lo + hi）
		int cmp = num - a[mid];
		
		if(cmp < 0){
			return rank1(num, lo, mid - 1);
		}else if(cmp > 0){
			return rank1(num, mid + 1, hi);
		}else{
			return mid;
		}
	}

这里很自然的采用了尾递归的形式：每次迭代的最后进入下一次迭代。递归的调用自己，直到找到或找不到最终的值。

尾递归的优势很明显：它易于理解，符合我们通常的思维习惯。

尾递归的劣势也很明显：在每次递归的调用下一次递归时，函数会保存上一次的上下文（传入参数，中间结果等），再将新调用的函数进行压栈。可是这里就存在了浪费，因为尾递归在原函数递归调用下一个函数以后会什么都不做（意味着之前保存的上下文没有作用）傻傻的等着递归调用的函数执行完成才能返回。

好在现代的编译器都很聪明：它们一般都可以自动的把尾递归转化为循环的形式，从而节约了宝贵的资源（保存执行方法的方法栈）。

好了，下面我们看下转化后的循环形式的二分查找是什么样子：

	//循环形式,num为待查数
	public static int rank2(int num, int lo, int hi){
		while(hi >= lo){
			int mid = lo + (hi - lo) / 2;
			int cmp = num - a[mid];
			if(cmp < 0){
				hi = mid - 1;
			}else if(cmp > 0){
				lo = mid + 1;
			}else{
				return mid;
			}
	}
		return lo;
	}

这种形式看起来就没有那么直观了，不过他们的思想都是一样的：不断的调用自己直到找到或找不到最终的值。循环让二分查找消去了函数的调用，而是直接在函数内部不断的改变参数。这样做的好处就是节省了空间。这里所有的变量空间都只分配了一次（它们的值在不断的变化）。所以相对于递归形式来说，消耗的空间约为其1/N(N为循环或迭代次数)。
3.算法分析

大家都知道二分查找的时间复杂度是lgn。可是这lgn是怎么来的呢？我们就以循环的实现方式来分析其时间复杂度。

分析时间复杂度时要找到执行频率最高的语句，在这里就是 ：

			int mid = lo + (hi - lo) / 2;
			int cmp = num - a[mid];
			if(cmp < 0){            //if结构算一句，因为它一次只会执行其中一个分支
				hi = mid - 1;
			}else if(cmp > 0){
				lo = mid + 1;
			}else{
				return mid;
			}

那么当最坏的情况下，当要查找一个长度为N的数组时，这几句代码要执行多少次呢？设执行次数为x，有N * (1/2)^x = 1 ，由此可以解出x = lgn（在算法分析中lgn都是以2为底的）。所以二分查找的时间复杂度为lgn。

在这放上一条结论：在N个键的有序数组中进行查找最多要进行lgn + 1 次比较。这里的+1是对应于查找不到元素的情况。有兴趣的话可以通过我后面给出的代码进行测试。

4.测试代码

public class BinarySearchTest {
	public static int[] a = {
			0,1,2,3,4,4,6,7,8,9
	};
	public static int[] b = {
			0,1,2,3,4,5,6,7,8,9
	};
	
	
	public static void main(String[] args) {
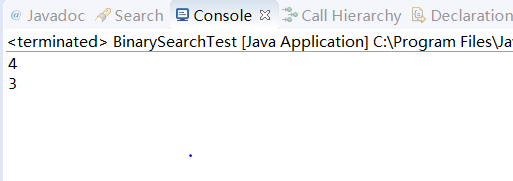
		System.out.println(rank1(5, 0 ,9, 0));
		System.out.println(rank2(5, 0 ,9, 0));
	}
	
	//尾递归形式,num为待查数
	public static int rank1(int num, int lo, int hi, int timeofCompare){
		if(hi < lo) return timeofCompare; //return lo;
		int mid = lo + (hi - lo) / 2;
		int cmp = num - a[mid];
		timeofCompare ++;
		if(cmp < 0){
			return rank1(num, lo, mid - 1, timeofCompare);
		}else if(cmp > 0){
			return rank1(num, mid + 1, hi, timeofCompare);
		}else{
			return timeofCompare; //return mid;
		}
	}
	//循环形式,num为待查数
	public static int rank2(int num, int lo, int hi, int timeofCompare){
		while(hi >= lo){
			timeofCompare++;
			int mid = lo + (hi - lo) / 2;
			int cmp = num - b[mid];
			if(cmp < 0){
				hi = mid - 1;
			}else if(cmp > 0){
				lo = mid + 1;
			}else{
				return timeofCompare; //return mid
			}
	}
		return timeofCompare;		//return lo
	}

}