KNN算法详解

K-Nearest Neighbor Classifiction

1. KNN算法是怎么来的？

   猜猜看：最后一行未知电影属于什么类型的电影？

电影名称	打斗次数	接吻次数	电影类型
Califomia Man	3	104	Romance
He's Not Really into Dudes	2	100	Romance
Beautiful Woman	1	81	Romance
Kevin Longblade	101	10	Action
Robo Slayer 3000	99	5	Action
Amped II	98	5	Action
Unkown	18	90	Unkown

如果我们把每部电影当作是平面上的一个点，打斗次数表示X坐标，接吻次数表示Y坐标，那么可以得到下面的点

点	X坐标	Y坐标	点类型
A点	3	104	Romance
B点	2	100	Romance
C点	1	81	Romance
D点	101	10	Action
E点	99	5	Action
F点	98	5	Action
G点	18	90	Unkown

   

再看另一个例子，想一想：下面图片中只有三种豆，有三个豆是未知的种类，如何判定他们的种类？

   

提供一种思路，即：未知的豆离哪种豆最近就认为未知豆和该豆是同一种类。由此，我们引出最近邻算法的定义：为了判定未知样本的类别，以全部训练样本作为挖个好看哦，计算未知样本与所有训练样本的距离，并以最近邻者的类别作为决策未知样本类别的唯一依据。但是，最近邻算法明显是存在缺陷的，我们来看下面这个例子。

   

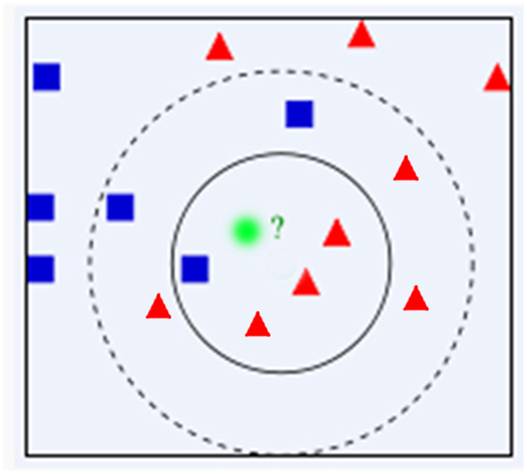
问题：有一个未知形状X（图中绿色的圆点），如何判断X是什么形状？

   如果采用最近邻算法，我们容易认为该图形为正方形。然而，在离该点稍远处有较多的三角形。或许，该未知点被认为是三角形更为合理。

   显然，通过上面的例子我们可以明显发现最近邻算法的缺陷——对噪声数据过于敏感，为了解决这个问题，我们可以把位置样本周边的最多个最近样本计算在内，扩大参与决策的样本量，以避免个别数据直接决定决策结果。由此，我们引进K-最近邻算法。

2. KNN算法的实现步骤

step.1 -- 初始化距离为最大值；

step.2 -- 计算未知样本和每个训练样本的距离dist；

step.3 -- 得到目前K个最临近样本中的最大距离maxdist；

step.4 -- 如果dist小于maxdist，则将该训练样本作为K-最近邻样本；

step.5 -- 重复步骤2、3、4，直到未知样本和所有训练样本的距离都算完；

step.6 -- 统计K个最近邻样本中每个类别出现的次数；

step.7 -- 选择出现频率最大的类别作为未知样本的类别。

3. KNN算法的缺陷

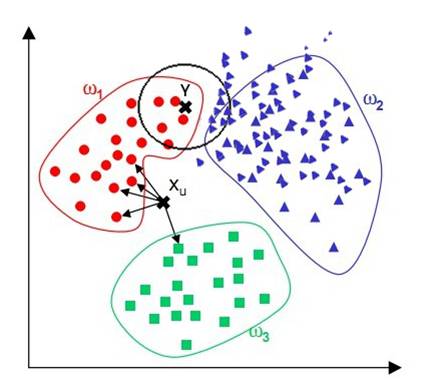
   观察下面的例子，我们看到，对于位置样本X，通过KNN算法，我们显然可以得到X应属于红点，但对于位置样本Y，通过KNN算法我们似乎得到了Y应属于蓝点的结论，而这个结论直观来看并没有说服力。

   由上面的例子可见：该算法在分类时有个重要的不中是，当样本不平衡时，即：一个类的样本容量很大，而其他类样本数量很小时，很可能导致当输入一个未知样本时，该样本的K个邻居中大数量类的样本占多数。但是这类样本并不接近目标样本，而数量小的这类样本很靠近目标样本。这个时候，我们有理由认为该位置样本属于数量小的样本所属的一类，但是，KNN却不关心这个问题，它只关心哪类样本的数量最多，而不去把距离远近考虑在内，因此，我们可以采用权值的方法来改进。

   和该样本距离小的邻居权值大，和该样本距离大的邻居权值相对较小，由此，将距离远近的因素也考虑在内，避免一个样本过大导致误判的情况。

   此外，从算法实现的过程中，该算法还存在两个严重的问题，第一个是需要存储全部的训练样本；第二个是需要进行繁复的距离计算。

 

5. KNN算法的MATLAB实现

<span style="font-size:18px;">clear all;
close all;
clc;
 
% 生成样本类1
mu1 = [0,0];
sigma1 = [0.8,0;0,0.6];
data1 = mvnrnd(mu1,sigma1,200);
label1 = ones(200,1);
plot(data1(:,1),data1(:,2),'o');
hold on;
 
% 生成样本类2
mu2 = [2.2,1.9];
sigma2 = [1.3,0;0,1.1];
data2 = mvnrnd(mu2,sigma2,200);
label2 = label1+1;
plot(data2(:,1),data2(:,2),'r+');
hold on;
 
% 样本和K值
data=[data1;data2];
label=[label1;label2];
K=10;
 
% 测试
for ii=-3:0.1:6
       forjj = -3 : 0.1 : 6
              test_data= [ii jj];
              label= [label1; label2];
              distance= zeros(400,1);
              %  计算未知点与样本点的距离
              fori = 1:400
                     distance(i)= sqrt((test_data(1)-data(i,1)).^2+(test_data(2)-data(i,2)).^2);
              end
             
      %  排序
              fori = 1:400
                     ma= distance(i);
                     forj = i+1:400
                            ifdistance(j)<ma
                                   ma= distance(j);
                                   label_ma= label(j);
                                   tmp= j;
                            end
                     end
                    
                     distance(tmp)= distance(i);
                     distance(i)= ma;
                     label(tmp)= label(i);
                     label(i)= label_ma;
              end
             
      %  统计最近K个样本中类1的个数
              num1= 0;
              fori = 1:K
                     iflabel(i) == 1
                            num1= num1 + 1;
                     end
              end
             
              num2= K - num1;
             
              ifnum1>num2
                  plot(ii,jj,'r*');
              else
                     plot(ii,jj);
              end
      
       end
end
 </span>