分治(Divide and Conquer)是递归程序设计当中,一种非常重要的算法设计思路。利用它我们可以设计出许多高效的算法,例如排序、查找、大数乘积、矩阵乘法以及语法分析等等。它的核心思想是将一个复杂的问题分解成类型相同且相互独立的小问题,然后将小问题的解汇总,最终解决大问题。
分治法的一般步骤
使用分治法进行算法设计的一般步骤如下:
1. 将问题分为子问题。这些子问题与原来问题的类型相同,但是规模更小;每个子问题的规模通常是相同的。(Divide)
2. 递归的解决这些子问题。(Conquer)
3. 恰当地结合这些子问题的解。(Combine)
在这些步骤当中,“Conquer”这个部分大多数时候是较为简单的,只需要递归地调用解决问题的函数自己就可以了。而“Divide”和“Combine”这两个部分,则很多时候是一个需要进行仔细设计的内容。
分治法的具体例子
归并排序(Merge Sort)是一个使用分治法的思路,进行算法设计的经典例子。这里以它为例子,对分治法的思想进行介绍。这里先把解决问题的思路用进行中文表述:
1. 将原始的数列分成数量相等的左右两个部分。(Divide)
2. 对左右两个部分进行归并排序。(Conquer)
3. 将左右两个部分的排序结果进行合并,得到最终排序好的数列。(Combine)
将上面的内容改写成伪代码,可以表述为:
sortedArray = mergeSort(array)
// array : input array of length n
// sortedArray : sorted output array of length n
if 1 == n
sortedArray = array;
return sortedArray;
end
// Divide
leftPart = array(1...n/2);
rightPart = array(n/2+1...n);
// Conquer
leftPartSorted = mergeSort(leftPart);
rightPartSorted = mergeSort(rightPart);
// Combine
sortedArray = merge(leftPartSorted, rightPartSorted);
return sortedArray;
在这个例子当中,我们可以看到“Divide”和“Conquer”这两个部分是相对简单的,而“Combine”这个部分则是一个需要我们考虑的问题,因为它的设计将决定整个算法的时间复杂度。所以现在需要解决的问题变为,如何高效地将两个有序数列合并成一个新的有序数列的问题。下面看一下我们怎样使用O(n)的时间复杂度来解决这个问题。
C = merge( A, B )
// A : input array of length nA
// B : input array of length nB
// C : output array of length n = nA + nB
i = 1;
j = 1;
for k = 1 to n
if A(i) < B(j)
C(k) = A(i);
i++;
else
C(k) = B(j);
j++;
end
end
return C;
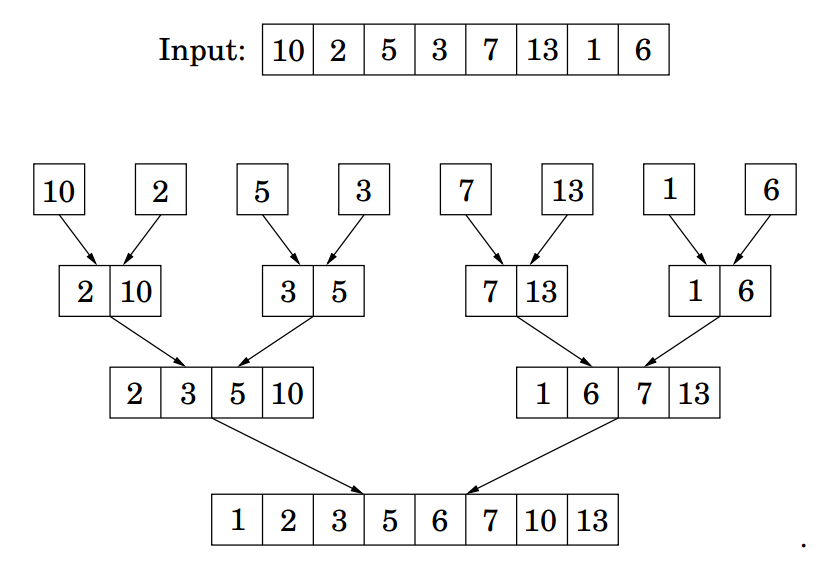
由于整个问题被分成了log2(n)层,每一层合并需要的时间复杂度为O(n),所以整个算法的时间复杂度便为O(nlog2(n))了,也可以等价简写为O(nlog(n))。下面是一个使用归并排序,解决具体问题的示意图:
分治法的算法复杂度分析
假设分治法“Divide”部分将规模n的问题分成了a个子问题,每个问题的规模为“n/b”,“Combine”子问题结果的时间复杂度为O(n^d),那么整个问题的时间复杂度会是怎么样呢。
一个叫Master theorem的定理给了我们下面一个估算时间复杂度的方法,这个可以使我们对设计的算法有一个宏观上的掌握。详细的推导过程可以根据上面的图来进行,比较容易。
其中T(n)表示整个算法的时间复杂度。在归并排序中,a = 2, b = 2, d = 1,故符合第二行的情况, 时间复杂度为O(nlog(n))。











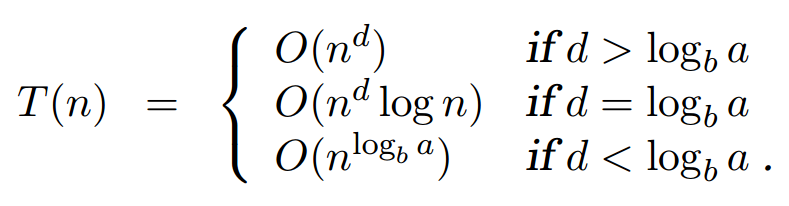















 432
432

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










