关于lucas定理的那些事儿

about 组合数

我们知道，$C_n^m$表示表示从 n 个元素中取出 m 个元素的方案数，在做数学题时，题目一般不会将n和m给到太大的数。所以我们一般会用以下公式：

$$C_n^m=\frac{n!}{m!\times (n-m)!}$$

在编程时，我们还会使用杨辉三角公式：

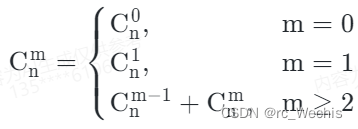
或者质因数分解求组合数：

我们需要计算 n!（n 的阶乘），即 n! = n × (n-1) × (n-2) ×… × 1。为了提高计算效率，我们可以利用质因数分解的方法将 n! 分解成若干个质数的乘积，如下所示：

$$n!=p{1}^{a}1\times p{2}^{a}2\times ...\times p{k}^{a}k$$

其中 p1, p2,…, pk 是 n 的质因数，a1, a2,…, ak 是相应质因数的指数。

接下来，我们将组合数计算公式 $C_n^m$ 改写为：

$$C_n^m=\frac{n!}{m!(n-m)!}$$

利用 n! 的质因数分解形式，可以将上式改写为：

$$C_n^m=\frac{p{1}^{a}1\times p{2}^{a}2\times ...\times p{k}^{a}k}{m!(n-m)!}$$

为了方便计算，我们可以将分母的 m! 和 (n-m)! 分别表示为质因数分解的形式：

$$m!=p{1}^{b1}\times p{2}^{b2}\times ...\times p{x}^{bx}$$

$$(n-m)!=q{1}^{c1}\times q{2}^{c2}\times ...\times q{y}^{cy}$$

其中 p1, p2,…, px 是 m 的质因数，b1, b2,…, bx 是相应
质因数的指数；q1, q2,…, qy 是 n-m 的质因数，c1,

c2,…, cy 是相应质因数的指数。

将分母的质因数分解形式代入组合数公式，得到：

$$C_n^m=\frac{p{1}^{a}1\times p{2}^{a}2\times ...\times pkak}{p1b1\times p{2}^{b}2\times ...\times p{x}^{b}x\times q{1}^{c}1\times q{2}^{c}2\times ...\times q{y}^{c}y}$$

接下来，我们可以约分分子和分母中的公共质因数，以得到组合数 C_{n}^{m} 的最简形式。

好了，我们已经介绍了求组合数的三种基本做法，现在你可以尝试拿到这一题的部分分了。

lucas 定理

很明显，这一题的数据有点大，如果用第一，三种，会TLE，用第二种，会MLE。

就像题目说的：

P3807 【模板】卢卡斯定理/Lucas 定理

我们知道，要用新算法了。

lucas 定理概念

lucas定理用来求$C_n^m\mathrm{mod}p$的值，其中p为素数。

lucas定理的公式为：

$$luca{s}_n^m=C_n^m\mathrm{mod}p=C_{n\mathrm{mod}p}^{m\mathrm{mod}p}\times luca{s}_{[\frac{n}{p}]}^{[\frac{m}{p}]}\mathrm{mod}p$$

证明：

引理1

$$C_p^x\equiv 0(\mathrm{mod}p)$$

引理1证明

根据$C_n^m=\frac{n!}{m!\times (n-m)!}$，得:
$$C_p^x=\frac{p!}{x!\times (x-p)!}$$
$$\therefore C_p^x=\frac{p\times (p-1)!}{x\times (x-1)!\times (p-x)!}$$

$$\therefore C_p^x=\frac{p}{x}\times \frac{(p-1)!}{(x-1)!\times (p-x)!}=\frac{p}{x}\times C_{p-1}^{x-1}$$

$$\therefore C_p^x=p\times inv(x)\times C_{p-1}^{x-1}$$
(inv(x)为x的逆元)
$$\therefore p|C_p^x$$

$\therefore 证毕$

引理2

$$(1+x{)}^p\equiv 1+x^p(\mathrm{mod}p)$$

引理2证明

我们知道：

$$\therefore (1+x{)}^p=1^p+1^{p-1}\times x+1^{p-2}\times x^2+...+x^p$$

$$=C_p^0\times 1^p+C_p^1\times 1^{p-1}\times x+...+C_p^p\times x$$

化简，得：

$$(1+x{)}^p=\sum _{i=0}^p{C}_p^i\times x^i$$

由引理1得$C_p^i\times x^i\equiv 0(\mathrm{mod}p)(i\ne 0,i\ne p)$

$$C_p^0\times x^0\times 1^p=1$$
$$C_p^p\times x^p\times 1^0=x^p$$
$$\therefore C_p^i\times x^i\mathrm{mod}p=(C_p^0\times x^0\times 1^p+C_p^p\times x^p\times 1^0)=1+x^p(\mathrm{mod}p)$$

$\therefore 得证$

lucas定理证明

令n=ap+b,m=cp+d

$$(1+x{)}^n\equiv \sum _{i=0}^n{C}_n^i\times x^i(\mathrm{mod}p)---->记为(1)$$
$$\equiv (1+x{)}^{ap+b}$$
$$\equiv ((1+x{)}^p{)}^a\times (1+x)b$$
结合引理2得：
$$\equiv (1+x^p{)}^a+(1+x{)}^b$$
$$\equiv \sum _{i=0}^a{C}_a^i\times x^{ip}\times \sum _{i=0}^b{C}_b^j\times x^j(\mathrm{mod}p)-->记为(2)$$

(1)中$x^m$的系数为$C_n^{i=m}=C_n^m$

(2)中$x^m$的系数为$C_a^c\times C_b^d$

$\therefore C_n^m\equiv C_a^c\times C_b^d(\mathrm{mod}p)$
$$\therefore C_n^m\equiv C_{n\mathrm{mod}p}^{m\mathrm{mod}p}\times C_{[\frac{n}{p}]}^{[\frac{m}{p}]}\equiv C_{n\mathrm{mod}p}^{m\mathrm{mod}p}\times luca{s}_{[\frac{n}{p}]}^{[\frac{m}{p}]}(\mathrm{mod}p)$$

$\therefore 得证$

about题目

知道了lucas的公式，求解这道题就很简单了吧。

#include<bits/stdc++.h>
#define int long long
using namespace std;
int t,n,m,p;
int ksm(int a,int b,int p){//a^b mod p
	int res=1;
	while(b){
		if(b&1)res=res*a%p;
		a=a*a%p;
		b>>=1;
	}
	return res;
}
int C(int n,int m,int p){
	if(n<m)return 0;
	if(m>n-m)m=n-m;//for example, C(3,2)=C(3,1) 
	//C(n,m) mod p = n! * (m! * (n-m)!)^(p-2)  mod p
	//             = n! / (n-m)! * (m!)^(p-2) mod p
	int r1=1,r2=1;
	for(int i=0;i<m;i++){
		r1=r1*(n-i)%p;
		r2=r2*(i+1)%p;
	}
	return r1*ksm(r2,p-2,p)%p;
}
int lucas(int n,int m,int p){
	//lucas(n,m)=c(n,m) mod p = C(n%p,m%p) * lucas(n/p,m/p)
	if(m==0)return 1;
	return C(n%p,m%p,p)*lucas(n/p,m/p,p)%p;
}
signed main(){
	cin>>t;
	for(int i=1;i<=t;i++){
		cin>>n>>m>>p;
		m=n+m;
		cout<<lucas(m,n,p)<<endl;
	}
	return 0;
}

其中，ksm(r2,p-2,p)是求r2的逆元。

码字不易，点下一个赞吧。