深入讨论机器学习 8 大回归模型的基本原理以及差异！-CSDN博客

本文链接：https://blog.csdn.net/red_stone1/article/details/116358728

作者 | 台运鹏

几乎每个机器学习从业者都知道回归，其中一些人可能认为这没什么大不了的，只是从参数之间的切换罢了。本文将阐明每种回归算法的细节，以及确切的区别。包括：

OLS
Weighted Least Squares
Lasso
Ridge
Polynomial Regression
Logistic regression
Support Vector Regression
Elastic Net
Bayesian Regression
RANSAC
Theil Sen
Huber Regression
Decision Tree Regression

1. 介绍

我们的数据：，我们打算从我们的数据集中训练一个模型，并在未知的测试集中测试它。算法性能良好的标准是错误低（从预测值到实际值的距离）。当涉及回归任务时，我们第一时间就会想到线性回归。

这个模型是线性的并且易于实现（图 1）。被叫做斜率并且被叫做截距。解释了当改变的时候改变的程度。意味着随机错误（白色噪音），一般说来都会被省略。

2. OLS

在机器学习中，我们经常通过优化目标函数来找出最好的模型。OLS(Ordinary Least Squares) 充当了一个很有效果的损失函数只要模型满足六个 OLS 的必要假设。那么它就能通过优化如下的函数来找到具有最小方差的无偏差模型。

2.1 首要的假设

• 线性

换句话说，只有直线是可以的。如果和之间的关系是非线性的，比如，那么整个模型就会烂掉。对付这种情况一般采用特征转换。和之间的关系会永远被改变如果采用这种方法。因此我们必须把和之间的 correlation 纳入考虑范围。我们可以通过计算（决策系数）来判断 correlation. 代表着我们能从预测出的能力。的那一列，括号里是原来未经改变的值（表 1），对于也一样。注意我用来生成了 10000 个随机点。代表的是噪音并且它的范围是从 0 到 1。遵循随机均匀分布。如果要更进一步实施特征转换， 多项式回归是一个不错的选择。

图1. 普通回归模型

表1. 改变结果

如表 1 所示，应用特征变换时发生变化，目的是找到具有最佳的线性模型。请注意，线性表示是相对于改变后的 。如果是这样，原始和预测的 的散点图应适合原始分布图。此假设对于线性回归最为重要，并且可以解释当和不满足线性关系的时候用 Ridge 或 Lasso 的效果也很差。

多项式回归用多项式替换原始的，以实现比以前更线性的关系或出于某些原因更改特征。有趣的是，它有点像泰勒展开式。当您的模型违反了线性，然后您可以尝试所有多项式回归找到最佳的，这是一个很好的方法。

如果特征维度是 2 维

图2. 可视化改变结果

• 常量误差方差这意味着残差是均匀分布的，在统计上称为无异方差当我们应用模型时，通过观察可以得到一堆预测值。然后我们可以计算出预测值和真实值之间的误差。我们还可以计算误差的方差。如果误差遵循正态分布，则其方差为常数（）。此外，其分布是对称的。残差的分布也应该是均匀和对称的，因此我们可以使用残差图进行检测（图 3），并且 QQ 图可以检测误差是否遵循正态分布。我使用的数据可以从这里下载：https://www.kaggle.com/quantbruce/real-estate-price-prediction。

我将 X2 house age 设为，将 Y house price of unit area 设为。请注意，我删除了等于 0 的点。我选择了 200 个点作为研究。

上面第2个式子表示标准正态分布，如图 3 所示，如果噪声遵循正态分布，则分布应均匀，如图（b）所示。直方图应该像钟形曲线。我们可以小心得出结论，即如果误差遵循正态分布，则噪声分布应适合 Q-Q 图中的线。

在弄清楚异方差性之后，我们不知不觉会想到一个问题，即异方差如何影响我们的模型以及如何对其进行改进。最常见的方法是尝试特征转换，例如 Log。如图 4 所示，它可以在某种程度上使我们的残差更加稳定。它始终是尝试的一种选择，但不是解决问题的有效方法。

Weighted Least Squares 的性能比 OLS 好得多。相对而言，当都等于 1 时，应该是 OLS。在 OLS 中，模型给每个点同样的注意力。但那是它位于无异方差下，而我们遇到更多有异方差的场景。我们的想法是给那些噪音小的点更多注意。因此，模型给那些点更大的权重。

注意，我为前 20 个权重选择了不同的值，其他权重值始终为 1。不同的权重等同于噪声的异常分布。如表 2 所示，模型仍为无偏见的，也就是说，截距始终为正确的。但是，斜率的标准偏差会急剧变化。因此，我们无法使用它来得出推论并检验关于斜率的假设。

如图 5 所示，图（a）表示权重 =1 时 OLS 是 MLS 的特例，而图（b）和图（c）表示权重变化时，截距几乎保持不变。

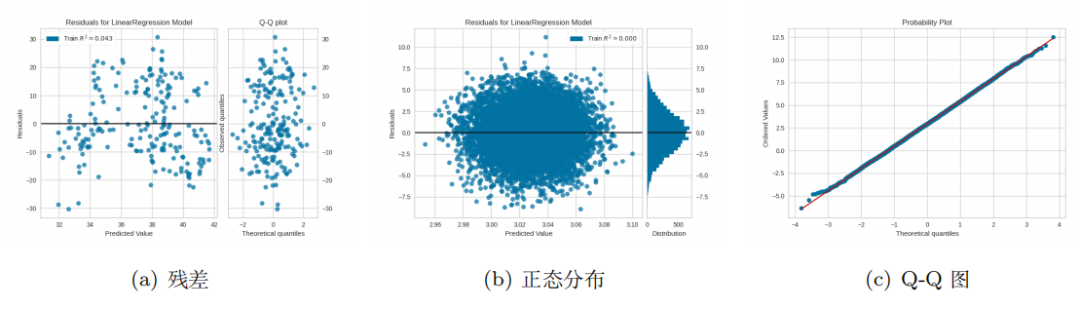
图3. 正态与非正态

表2. 斜率和截距

而且，我们可以应用 Box Cox 特征转换，它可以使数据更接近正态分布。可以从这里下载数据：https://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-white.csv。我选择 total sulfur dioxide 作为 X，quality 作为 y. 因此，它可以减轻异方差（图 6）。请注意，并非总是如此一个很好的解决方案。但是我们可以在 WLS 之前尝试使用它们。有时候，情况可能更糟（图 7）。

• 错误独立分布（无自相关）。例如，您要预测股票市场中的市场份额。但错误是相关的，而它们本应为（独立分布）。当发生金融危机时，股票的份额将在未来几个月内减少。可以通过 Durbin Watson Test（表 3）或绘制 textbf 自相关图进行检测。如果 y 的值位于在，则为正相关。如果值等于 0，则它们的含义是无相关。否则，它们的含义是负相关。

表3. Durbin Watson Test

自相关会影响标准差，但不太可能影响模型的系数和截距。

有两种常见的解决方法。第一种方法是添加被忽律的变量。例如，您想按时间预测股票表现。无疑，该模型具有很高的自相关性。但是，我们可以添加 S ＆ P 500。希望它可以减轻自相关。第二种方法是改变模型函数。您可以将线性模型转换为平方模型。另外，也别忘了多项式回归。

无多重共线性。如果自变量彼此相关，则数据中存在多重共线性。我们可以使用方差膨胀因子（VIF）进行检测（是决策系数）。如果值为 1，表示预测变量之间不存在多重共线性。如果值大于 5，则表示存在潜在的多重共线性。如果值大于 10，则表示明显的多重共线性。

图4. Log 和残差之间的关系

我们回归模型的目标是通过找到合适的系数来找出自变量（）与 因变量（）之间的关系。但是当存在多重共线性时，该系数无法被解释出来。我们实际上不知道确切的关系是什么。但是，如果我们只想进行好的预测，它仍然有效。并且如果多重共线性的程度适中，则不必太在意。我们可以删除高度相关的变量或增加样本容量。

• 无外生性。如果我们选择的对几乎没有影响，这意味着真实的预测不是基于而是，则存在外生性。最佳解决方案是要搞清楚到底哪些因素会影响我们的预测值，然后选择合适的。

3. Lasso Regression

3.1 Background

在机器学习中，我们采用我们的模型通过对大量数据进行训练来预测值。但是，对过多数据进行训练会产生一个副产品，即机器可能会记住所有训练数据。当涉及到新的测试数据时，我们的机器无法对其进行正确的估算，这称为过拟合。实际上，我们不知道到底需要多少数据。如果缩减数据量，则可能会导致 textbf 欠拟合。因此，我们必须更改模型。

3.2 稀疏方法

在这里，我们使用均方误差。最初，我们需要使模型的误差尽可能小，这可能会导致复杂的模型（太多系数）。通常，如果我们的模型是太复杂了，它的泛化能力很低。为了解决这个问题，出现了正则化。代表我们要惩罚模型的程度（变简单）。通过添加 L1 常项，我们将选择一个误差最小的简单模型，该模型与奥卡姆剃刀原则一致。L1 可能把许多系数设置为。不可避免地，某些特征会因此失去对的影响， L1 真正要做的是执行特征选择。

3.3 震荡

梯度下降在使目标函数最小化中起着关键作用。在优化过程中，L1 总是减去常数。因此，当数据值很小时，L1 尤为重要。L1 执行特征选择，不稳定并可能导致震荡。

图5. 中间那条显示 OLS 和 MLS 拟合情况数据，其他是两个算法的预测值范围

4. Ridge Regression

4.1 背景

尽管 Lasso 能够处理过拟合，但它缺乏稳定性。因此，Ridge 是 Lasso 的替代方案。

4.2 稳定性

为什么 Ridge 比 Lasso 更稳定？例如，通过最小二乘法得到模型。这很复杂。使用 Lasso 可以得到虽然我们可以通过 Ridge 获得。Ridge 要求每个系数都尽可能小，但是不会激烈到设置某些系数为 0。

4.3 更好的选择

同样，它使用梯度下降。但是 Lasso 和 Ridge 之间的区别是 Ridge 不是减去常数而是系数向量。假设我们在一座山顶上，Lasso 所做的只是往前挪了一小步，而 Ridge 就看哪个方向比较陡，就直接迈出一大步，因此，Ridge 比 Lasso 更快。当值很大时，Ridge 应该是比 Lasso 更好的选择。总而言之，从稳定性和速度的角度来看，Ridge 比 Lasso 来得好，如图 8。

图6. Box Cox 改变可能有帮助

5. Elastic Net Regression

Elastic Net 是 Ridge 回归和 Lasso 回归之间的中间地带。它将 Lasso 的损失函数与 Ridge 的损失函数混合在一起。它的参数控制混合比例。如果，则为 Ridge.If ，是 Lasso。那么什么时候使用 Lasso，Ridge 或 Elastic Regression？在大多数情况下，Ridge 是一个很好的默认设置。如果您的数据具有太多特征（例如，深度学习），则某些特在没有意义。因此，我们希望删除某些特在。但实际上，我们不知道要删除哪些特征。Lasso 充满风险。如果某些特征是相关的（多重共线性），则 Elastic Net Regression 是最佳选择。它不太可能将某些参数设置为零。它可能对某些相关的自变量进行聚类。

6. Robust Regression

6.1 Background

数据并不总是很好，可能包括一些异常值。因为机器不知道存在异常值，所以它仍然给予它们同样的关注。因此，异常值可能会破坏模型。这就是 Robust Regression 被提出的原因。

6.2 RANSAC

图7. Box Cox 改变可能更糟糕

随机抽样一致是鲁棒回归模型之一。通过不断重新估计，RANSC 使用共识集（Inliers Set）的所有成员来提高准确性。

6.3 Theil-Sen Regression

这是一种无参数方法，这意味着它无需对数据的分布进行任何假设。它还具有一个临界情况（通常为 29.3 % ），表明它只能容忍异常值分布的最大值为 29.3 %。

6.4 Huber Regression

当值很大时，Huber 会将其损失函数转换为线性损失，以最大程度地减少对模型的影响。作为阈值，决定多大的数据需要给予线性损失。

7. Bayesian Regression

7.1 Bayesian Theorem

例如，我们将采用一个模型来区分电子邮件是正常的还是垃圾邮件。因此，我们的模型所面对的是它必须对未知电子邮件进行预测。我们的数据包含 100 封电子邮件，其中 10% 是垃圾邮件。因此，垃圾邮件的百分比为 10 。但这绝对不是全部。在贝叶斯中，它称为前验概率，这代表着分布的基础假设，同时这也是贝叶斯开始的地方。在算法开始时，贝叶斯是有偏见的，所以该模型很容易受到一开始的数据分布的影响。例如，如果我们只有 10 封普通电子邮件，我们未来是不可能不收到一封垃圾邮件的。换句话说，如果我们的数据量很小，就不太建议实施贝叶斯算法。但是，不断进行数据训练，我们最终应该会获得理想的结果。下面的等式，P（B）是归一化项，P（A）是前验概率。是后验概率。总而言之，当我们拥有大量数据时，贝叶斯算法可能是一个很好的选择，它可以像其他算法一样准确地执行。

7.2 MLE

一般来说，我们的目标是找出真正的数据分布，这几乎是不可能的。因此，我们需要一个与问题域的数据分布更接近的数据分布。MLE（最大似然法）。它表示我们希望最大化从假设分布采样出真正分布在数据集中的数据的概率。（图 9）

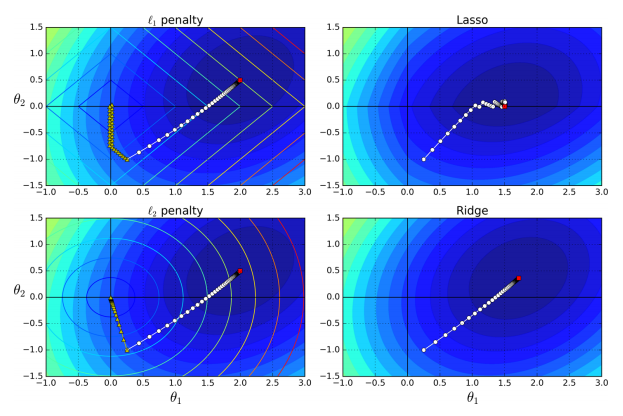
图8. Lasso VS Ridge

7.3 MAP

通常，我们可以使用 MAP 最大化后验概率）替换 MLE。它基于贝叶斯定理。MAP 是 贝叶斯回归 （下式）的基础。贝叶斯回归不像其他算法，它不会生成单个值，而是生成可能的分布范围。在大多数情况下，MLE 和 MAP 可能会得到相同的结果。但是，当 MAP 的假设为与 MLE 不同，它们无法获得相同的结果。当先验概率服从均匀分布时，它们可以获得相同结果。从另一个角度来看，如果我们对数据有精确的理解，则贝叶斯回归为一个很好的选择，因为它可以作为先验概率，或者我们可以像 Weighted Least Errors 一样给每个不同的选择不同的权重。有趣的是，前验分布可以看作是正则化或模型的偏见，因为前验分布可以是改为 L2 范数，这种模型也被称为贝叶斯岭回归。下式表示给定模型 m，输出 y 的概率。以及和（标准差）是任意值。

8. Support Vector Regression

8.1 最大化边际

支持向量机最初是为分类问题发明的。与其他算法不同，SVM 不仅需要正确分类所有数据，还需要数据到超平面的距离最大。如果我们的。我们的线性模型为。数据点，离超平面最经的分别带有正负标签的点到超平面的距离相加为边界（）。然后将 SVM 转换为最大化边界。我们可以将最大化变为最小化。因为大于 0，比大。除分类线外，SVM 还具有两条虚线。SVM 有两种类型。所有数据点都必须正确分类，这被称为 Hard Margin，这是不现实的，因为 Hard Margin 容易导致过拟合，而 Soft Margin 可以容忍一些错误，此方法听起来更可靠，与实际情况相符。