正态分布(Normal distribution)又名高斯分布(Gaussian distribution),是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。
若随机变量X服从一个数学期望为μ、标准方差为σ2的高斯分布,记为:X∼N(μ,σ2),
则其概率密度函数为
-
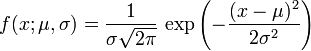
-
-
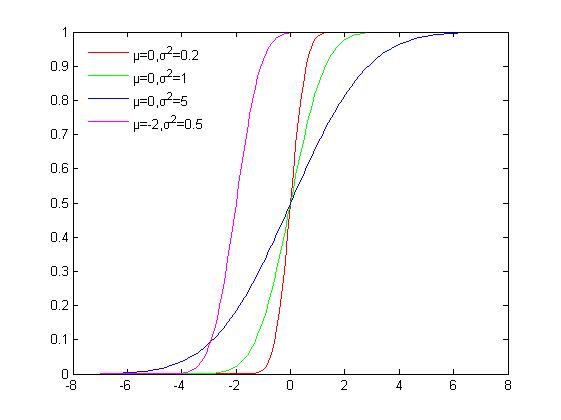
累积分布函数
累积分布函数是指随机变量X小于或等于x的概率,用密度函数表示为

- matlab实现代码
-
function [ output_args ] = Normpropogation( input_args ) %NORM PROPOGATION Summary of this function goes here % Detailed explanation goes here x=-7:0.1:7; y1=normpdf(x,0,1); y2=normpdf(x,0,0.45); y3=normpdf(x,0,2.23); y4=normpdf(x,-2,0.71); %线型,颜色,点型,线宽 figure; plot(x,y2,'-r','LineWidth',1); hold on; plot(x,y1,'-g','LineWidth',1); hold on; plot(x,y3,'-b','LineWidth',1); hold on; plot(x,y4,'-m','LineWidth',1); hold on; % legend('','','','',1); legend('μ=0,σ^2=0.2','μ=0,σ^2=1','μ=0,σ^2=5','μ=-2,σ^2=0.5',2); legend boxoff; figure; z1=normcdf(x,0,0.45); z2=normcdf(x,0,1); z3=normcdf(x,0,2.23); z4=normcdf(x,-2,0.71); plot(x,z1,'-r',x,z2,'-g',x,z3,'-b',x,z4,'-m'); h=legend('μ=0,σ^2=0.2','μ=0,σ^2=1','μ=0,σ^2=5','μ=-2,σ^2=0.5',2); legend boxoff; end
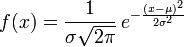
正态分布的期望值μ决定了其位置,其标准差σ决定了分布的幅度。因其曲线呈钟形,因此人们又经常称之为钟形曲线。我们通常所说的标准正态分布是μ = 0,σ = 1的正态分布(见右图中绿色曲线)。
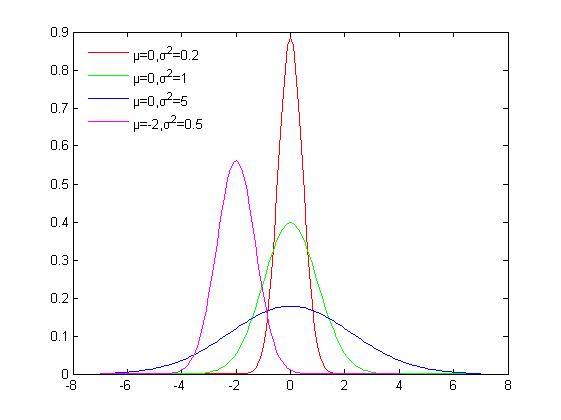
正态分布的概率密度函数均值为μ 方差为σ2 (或标准差σ)是高斯函数的一个实例:
























 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








