Apollo 10.0 Public Road Planner 详解（Planning代码学习）（四）

路径规划算法总体介绍

Apollo路径规划算力总体可以包含以下几个部分：

1. 路径决策
2. 路径优化
3. 速度决策
4. 速度优化

---

以上按照顺序执行

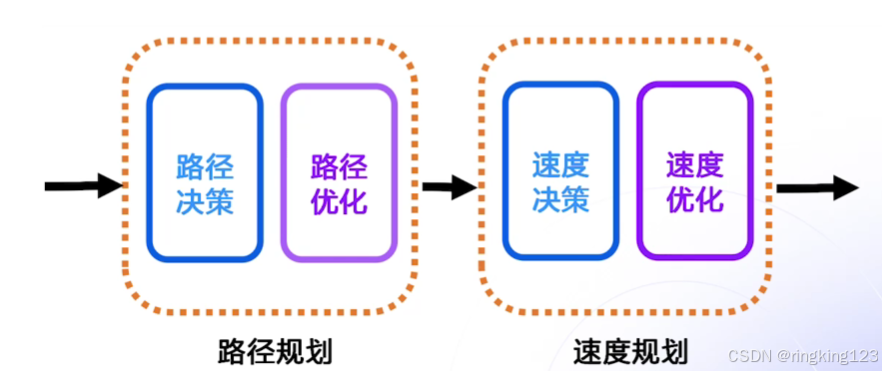
路径规划三部曲

LANE_FOLLOW_PATH任务

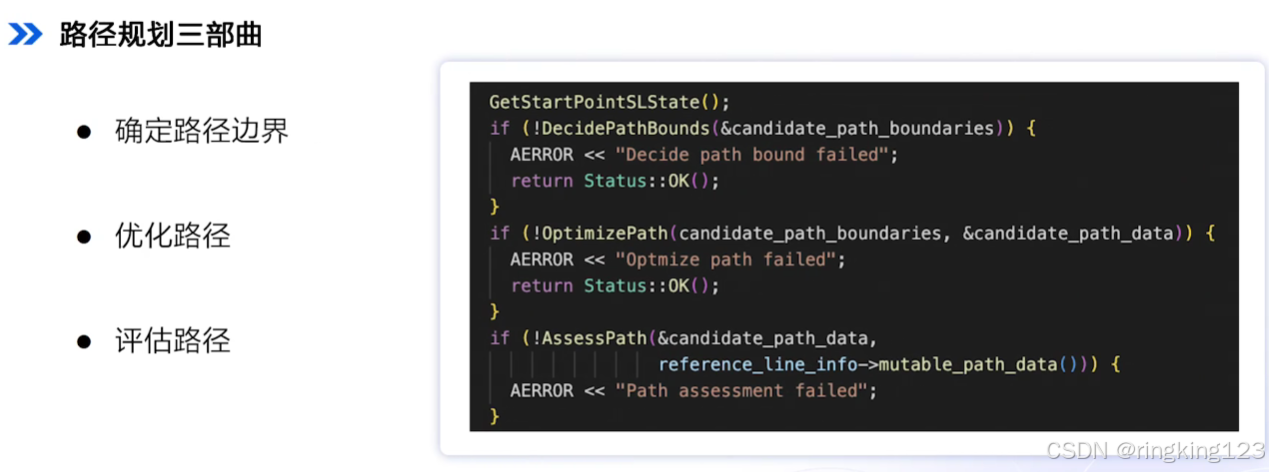
LANE_BORROW_PATH任务

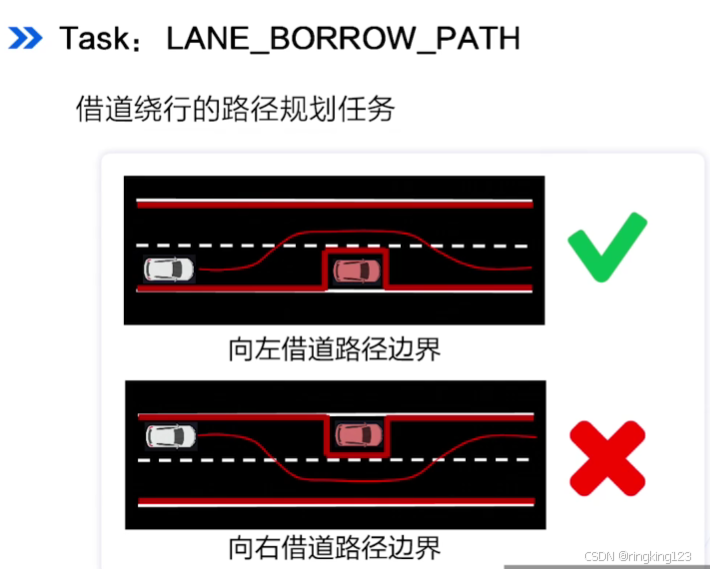
LANE_CHANGE_PATH任务

路径二次规划问题

二次规划的标准型如下
$$\begin{array}{rl}& \mathrm{minimize}\frac{1}{2}{x}^{T}Px+q^{T}x\\ & \mathrm{subject}\mathrm{to}l\le Ax\le u\\ & x\in {\mathbf{R}}^{n}P\in {\mathbf{S}}_{+}^{n}q\in {\mathbf{R}}^n\end{array}$$
目前求解二次规划问题使用基于ADMM的osqp算法。

定义优化变量

给出参考线：

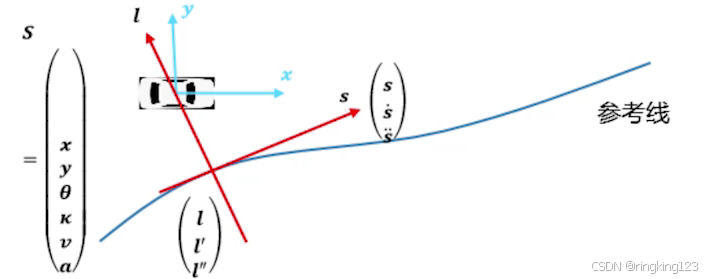
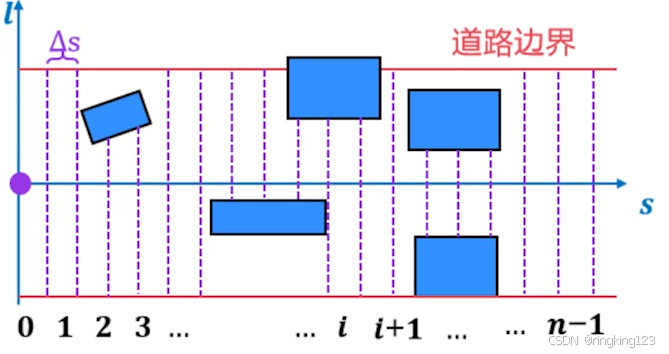
将障碍物投影到为frenet坐标系上：

定义$l^{\prime }=\frac{dl}{ds}$
间隔$\Delta s$将参考线离散化：
$$\begin{array}{ccccccccccccc}{l}_0& & & l_1& & & l_2& & & l_{n-2}& & & l_{n-1}\\ l_0^{\prime }& \stackrel{\Delta s}{\to }& & l_0^{\prime }& \stackrel{\Delta s}{\to }& & l_2^{\prime }& \dots & & l_{n-2}^{\prime }& \stackrel{\Delta s}{\to }& & l_{n-1}^{\prime }\\ l_0^{\prime \prime }& & & l_0^{\prime \prime }& & & l_2^{\prime \prime }& & & l_{n-2}^{\prime \prime }& & & l_{n-1}^{\prime \prime }\end{array}$$

$$x=\left\{\begin{array}{c}{l}_0,l_1,\dots ,l_{n-1},l_0^{\prime },l_1^{\prime },\dots ,l_{n-1}^{\prime },l_0^{\prime \prime },l_1^{\prime \prime },\dots ,l_{n-1}^{\prime \prime }\end{array}\right\}$$

确定优化函数

• 确保安全、礼貌的驾驶，贴近车道中心线 ：
  $$|l_i|\downarrow$$
• 确保舒适的体感，尽量降低横向速度/加速度/加加速度：
  $$|l_i^{\prime }|\downarrow ,|l_i^{\prime \prime }|\downarrow ,|l_{i\to i+1}^{\prime \prime \prime }|\downarrow$$
• 确保终点接近参考点：
  $$l_{end}=l_{ref}$$

因为是二次规划，采用二范数作为损失函数，其目标函数为：
$$\begin{array}{rl}& minf=\sum _{i=0}^{n-1}{w}_{ref}(l_i-l_{i-ref}{)}^2+w_l{l_i}^2+w_{dl}{l}_i^{\prime }\\ & \end{array}$$