B3695 集合运算 3
题目背景
关于集合、交集、并集的定义请参考 https://www.luogu.com.cn/problem/B3633。
以下给出对称差的定义:
对两个集合
A
,
B
A, B
A,B,规定
A
A
A 和
B
B
B 的对称差
A
Δ
B
A \Delta B
AΔB 为在
A
A
A 中出现但不在
B
B
B 中出现,或在
B
B
B 中出现但不在
A
A
A 中出现的元素。
例如,
A
=
{
1
,
2
,
3
}
A = \{1, 2, 3\}
A={1,2,3},
B
=
{
2
,
3
,
5
}
B = \{2, 3, 5\}
B={2,3,5},则
A
Δ
B
=
{
1
,
5
}
A \Delta B = \{1, 5\}
AΔB={1,5}
题目描述
给定 n n n 个集合 s 1 , s 2 , … s n s_1, s_2, \dots s_n s1,s2,…sn,每个集合都含有 [ 1 , m ] [1, m] [1,m] 之间的若干个整数。
现在,有 q q q 次操作,每次操作如下:
1 x y:将 s x s_x sx 中的每个元素都加上 y y y,再删去其中大于 m m m 的;2 x y:将 s x s_x sx 中的每个元素都减去 y y y,再删去其中小于 1 1 1 的;3 x y:查询 s x s_x sx 和 s y s_y sy 的交集的元素个数;4 x y:查询 s x s_x sx 和 s y s_y sy 的并集的元素个数;5 x y:查询 s x s_x sx 和 s y s_y sy 的对称差的元素个数;
输入格式
第一行有三个数,依次表示集合的个数 n n n,集合元素的最大值 m m m 和操作次数 q q q。
第
2
2
2 到第
(
n
+
1
)
(n + 1)
(n+1) 行,每行有若干个整数,第
(
i
+
1
)
(i + 1)
(i+1) 行的整数描述集合
i
i
i 的元素:
每行首先有一个整数
c
i
c_i
ci 表示
s
i
s_i
si 的元素个数,接下来有
c
c
c 个互不相同的整数
s
i
,
1
,
s
i
,
2
,
…
s
i
,
c
i
s_{i,1}, s_{i,2}, \dots s_{i, c_i}
si,1,si,2,…si,ci 表示集合
s
i
s_i
si 里的元素。
接下来 q q q 行,每行三个整数 o , x , y o, x, y o,x,y,表示一次操作。具体见『题目描述』。
输出格式
对于每个查询操作,请输出一行一个整数表示答案。
输入输出样例 #1
输入 #1
2 5 5
3 1 2 3
4 1 2 4 5
1 2 1
2 1 1
3 1 2
4 1 2
5 1 2
输出 #1
1
4
3
说明/提示
数据规模与约定
对于全部的测试点,保证 1 ≤ n , m , q ≤ 3 × 1 0 4 1 \leq n,m,q \leq 3 \times 10^4 1≤n,m,q≤3×104, 1 ≤ ∑ i = 1 n c i ≤ 1 0 6 1 \leq \sum_{i = 1}^n c_i \leq 10^6 1≤∑i=1nci≤106, 1 ≤ x , y ≤ n 1 \leq x, y \leq n 1≤x,y≤n, 1 ≤ o ≤ 5 1 \leq o \leq 5 1≤o≤5。集合里的元素都是不超过 m m m 的正整数。
感谢 @Zyingyzzz 提供 hack 数据一组。
C++实现
#include <bitset>
#include <vector>
#include <iostream>
const int maxn=30005;
int n,m,q;
std::bitset<maxn> s[maxn];
int main(){
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cin>>n>>m>>q;
for(int i = 1,c,x;i<=n; i++){
for(std::cin>>c;c;--c){
std::cin>>x;
s[i].set(x-1,1);
}
}
for(int i = 0; i<m; i++) s[0].set(i,1);
for(int o,x,y;q;--q){
std::cin>>o>>x>>y;
if(o==1){
s[x]<<=y;
s[x]&=s[0];
}else if(o==2){
s[x]>>=y;
}else if(o==3){
std::cout<<(s[x]&s[y]).count()<<'\n';
}else if(o==4){
std::cout<<(s[x]|s[y]).count()<<'\n';
}else if(o==5){
std::cout<<(s[x]^s[y]).count()<<'\n';
}
}
return 0;
}
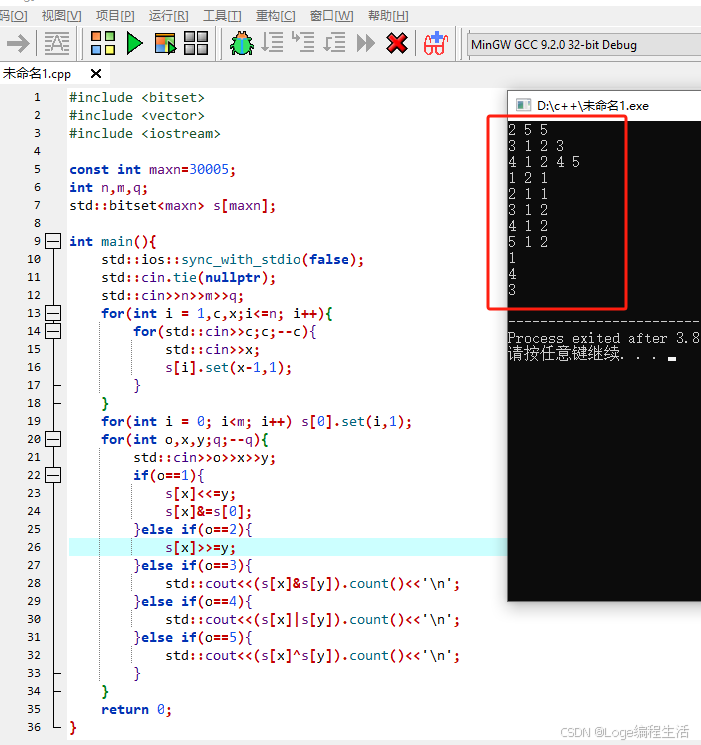
后续
接下来我会不断用C++来实现信奥比赛中的算法题、GESP考级编程题实现、白名单赛事考题实现,记录日常的编程生活、比赛心得,感兴趣的请关注,我后续将继续分享相关内容





















 7万+
7万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








