打卡信奥刷题（2568）用C++实现信奥 P2222 [HNOI2001] 矩阵乘积

最新推荐文章于 2025-12-21 21:47:42 发布

原创最新推荐文章于 2025-12-21 21:47:42 发布 · 654 阅读

15 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #算法 #开发语言 #数据库 #青少年编程

C++ 专栏收录该内容

2600 篇文章

订阅专栏

P2222 [HNOI2001] 矩阵乘积

题目描述

已知矩阵：

$Am×n=[a1,1a1,2⋯a1,na2,1a2,2⋯a2,n⋮⋮⋱⋮am,1am,2⋯am,n],Bn×p=[b1,1b1,2⋯b1,pb2,1b2,2⋯b2,p⋮⋮⋱⋮bn,1bn,2⋯bn,q]A_{m\times n}=\begin{bmatrix}a_{1,1} & a_{1,2} & \cdots & a_{1,n}\\ a_{2,1} & a_{2,2} & \cdots & a_{2,n} \\ \vdots & \vdots & \ddots & \vdots\\ a_{m,1} & a_{m,2} & \cdots &a_{m,n} \end{bmatrix} ,B_{n\times p}=\begin{bmatrix}b_{1,1} & b_{1,2} & \cdots & b_{1,p}\\ b_{2,1} & b_{2,2} & \cdots & b_{2,p} \\ \vdots & \vdots & \ddots & \vdots\\ b_{n,1} & b_{n,2} & \cdots &b_{n,q} \end{bmatrix}$

当矩阵 $A$ 的列数与矩阵 $B$ 的行数相同时，则 $A$ 与 $B$ 可以相乘，其乘积为一个 $m×pm\times p$ 的矩阵 $D$ ：

$Dm×p=[d1,1d1,2⋯d1,pd2,1d2,2⋯d2,p⋮⋮⋱⋮dm,1dm,2⋯dm,p]D_{m\times p}=\begin{bmatrix} d_{1,1} & d_{1,2} & \cdots & d_{1,p}\\ d_{2,1} & d_{2,2} & \cdots & d_{2,p} \\ \vdots & \vdots & \ddots & \vdots\\ d_{m,1} & d_{m,2} & \cdots & d_{m,p}\end{bmatrix}$

其中 $di,j=∑k=1nai,k×bk,jd_{i,j}=\sum^n_{k=1} a_{i,k} \times b_{k,j}$ ，简记为 $D=A×BD=A\times B$ 。

现已知三个矩阵 $A, B, C$ ，这三个矩阵大多数元素为 $0$ ，我们把这种矩阵称为稀疏矩阵。因此，我们采用三元组 $i, j, a$ 来表示矩阵的第 $i$ 行第 $j$ 列的值为 $a$ 其余未列出的元素均为 $0$ ；在计算机中，我们仅给出非零元素的三元组，而且使用行优先法给出稀疏矩阵的三元组，首先是第一行按列给出，然后是第二行按列给出……

例如，矩阵： $[1000002−101230000]\begin{bmatrix}1&0&0&0\\0&0&2&-1\\0&1&2&3\\0&0&0&0\end{bmatrix}$ 那么，矩阵的三元组表示为：

你的任务就是：计算矩阵 $D=A×B×CD=A\times B\times C$ 。

输入格式

第一行为两个正整数 $x, y$ ，分别表示输出结果所在的行和列。

第二行为四个整数 $m, n, o, p$ ，表明 $A$ 为 $m×nm\times n$ 的矩阵， $B$ 为 $n×on\times o$ 的矩阵， $C$ 为 $o×po\times p$ 的矩阵。

第三行以后的每一行有三个整数分别是矩阵的三元组表示法中的一个元素的值，每个矩阵之间有一个空行。表示的顺序是矩阵 $A, B, C$ 。

输出格式

仅一个整数，为 $D$ 的第 $x$ 行第 $y$ 列的元素的值。

输入输出样例 #1

输入 #1

输出 #1

说明/提示

数据规模与约定

对于全部的测试点，保证 $1≤m,n,o,p≤6×1031\le m,n,o,p\le 6\times 10^3$ ，三元数组的总个数不大于 $6×1036\times 10^3$ 。数据之间用空格分开。

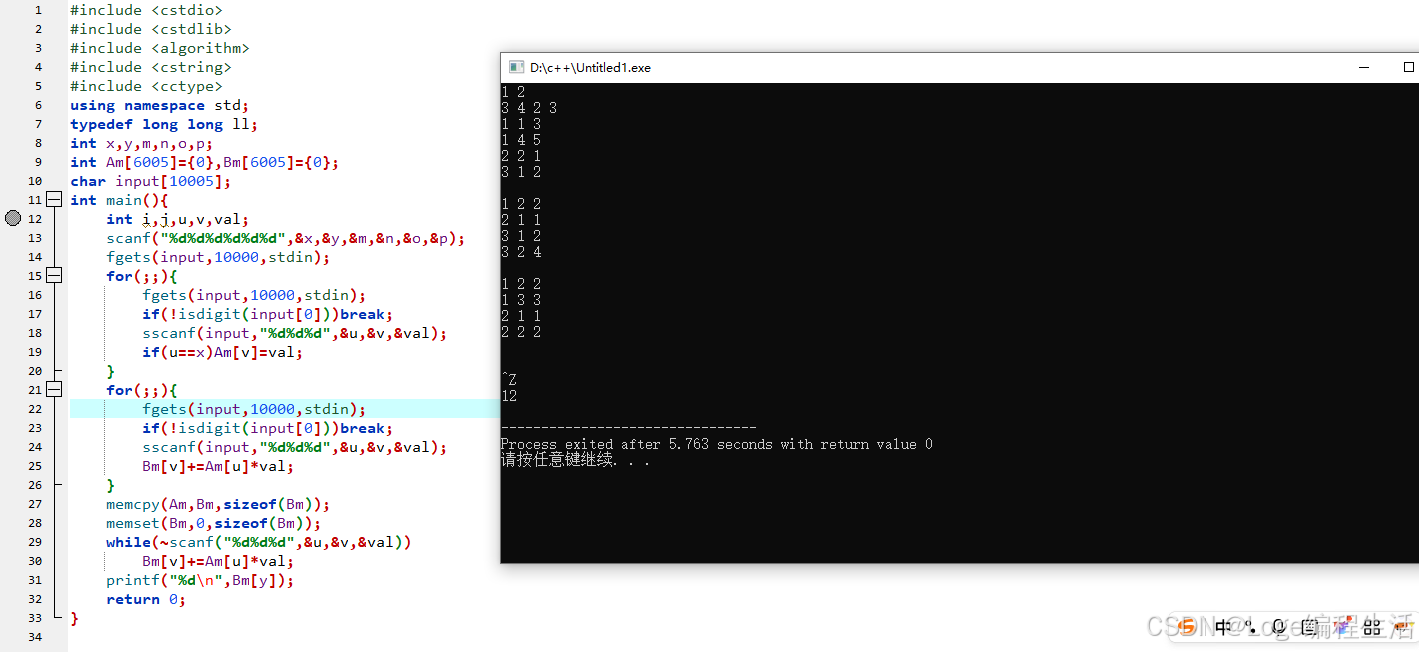
C++实现

#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cstring>
#include <cctype>
using namespace std;
typedef long long ll;
int x,y,m,n,o,p;
int Am[6005]={0},Bm[6005]={0};
char input[10005];
int main(){
    int i,j,u,v,val;
    scanf("%d%d%d%d%d%d",&x,&y,&m,&n,&o,&p);
    fgets(input,10000,stdin);
    for(;;){
        fgets(input,10000,stdin);
        if(!isdigit(input[0]))break;
        sscanf(input,"%d%d%d",&u,&v,&val);
        if(u==x)Am[v]=val;
    }
    for(;;){
        fgets(input,10000,stdin);
        if(!isdigit(input[0]))break;
        sscanf(input,"%d%d%d",&u,&v,&val);
        Bm[v]+=Am[u]*val;
    }
    memcpy(Am,Bm,sizeof(Bm));
    memset(Bm,0,sizeof(Bm));
    while(~scanf("%d%d%d",&u,&v,&val))
        Bm[v]+=Am[u]*val;
    printf("%d\n",Bm[y]);
    return 0;
}