打卡信奥刷题（2570）用C++实现信奥 P2233 [HNOI2002] 公交车路线

P2233 [HNOI2002] 公交车路线

题目描述

在长沙城新建的环城公路上一共有 $8$ 个公交站，分别为 A、B、C、D、E、F、G、H。公共汽车只能够在相邻的两个公交站之间运行，因此你从某一个公交站到另外一个公交站往往要换几次车，例如从公交站 A 到公交站 D，你就至少需要换 $3$ 次车。

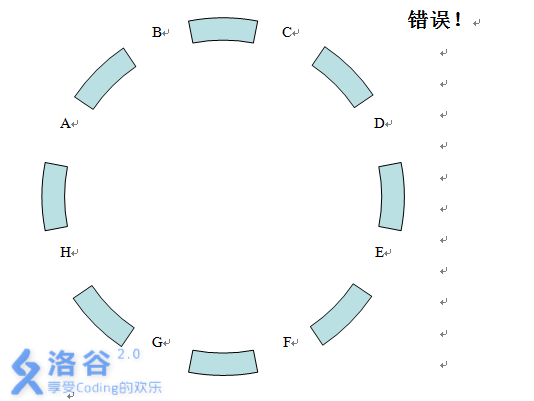
Tiger 的方向感极其糟糕，我们知道从公交站 A 到公交 E 只需要换 $4$ 次车就可以到达，可是 tiger 却总共换了 $n$ 次车，注意 tiger 一旦到达公交站 E，他不会愚蠢到再去换车。现在希望你计算一下 tiger 有多少种可能的乘车方案。

输入格式

仅有一个正整数 $n$，表示 tiger 从公交车站 A 到公交车站 E 共换了 $n$ 次车。

输出格式

输出一个正整数表示方案数，由于方案数很大，请输出方案数除以 $1000$ 后的余数。

输入输出样例 #1

输入 #1

6

输出 #1

8

说明/提示

8 条路线分别是：

(A→B→C→D→C→D→E)，(A→B→C→B→C→D→E)，

(A→B→A→B→C→D→E)，(A→H→A→B→C→D→E)，

(A→H→G→F→G→F→E)，(A→H→G→H→G→F→E)，

(A→H→A→H→G→F→E)，(A→B→A→H→G→F→E)。

数据范围

$4\le n\le 10^7$。

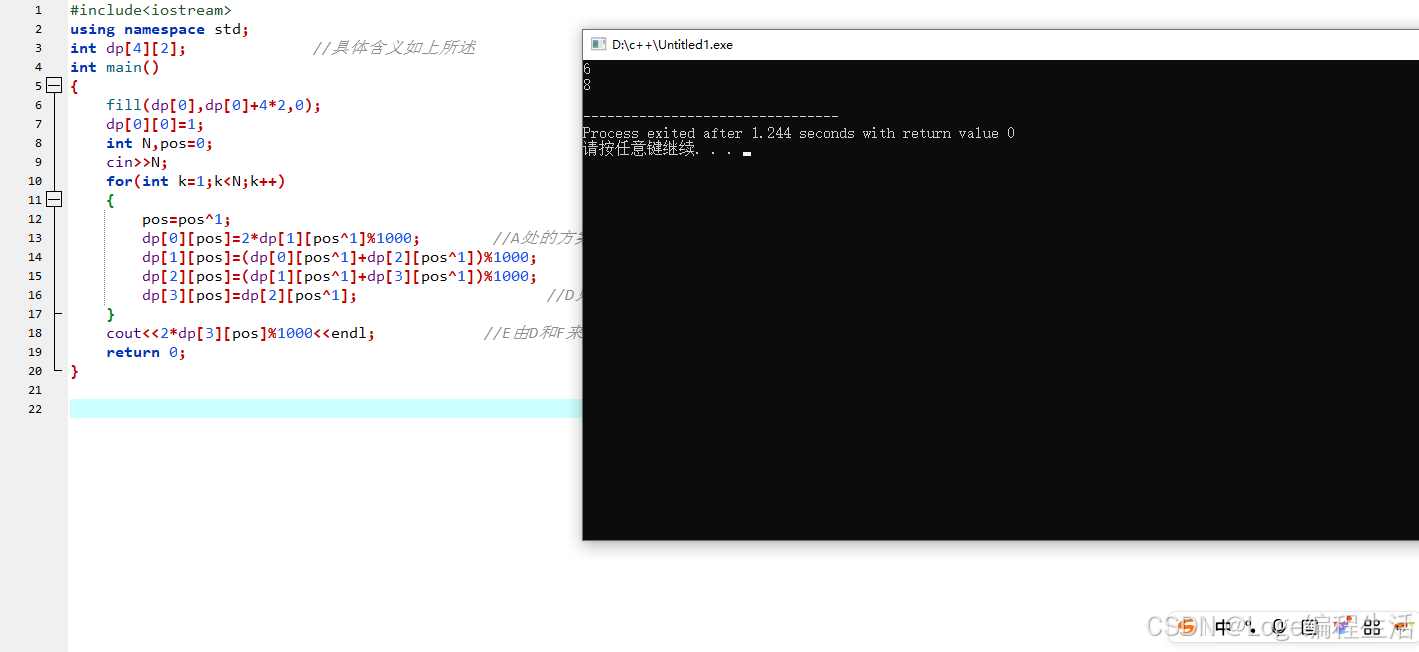
C++实现

#include<iostream>
using namespace std;
int dp[4][2];              //具体含义如上所述
int main()
{
    fill(dp[0],dp[0]+4*2,0);
    dp[0][0]=1;
    int N,pos=0;
    cin>>N;
    for(int k=1;k<N;k++)
    {
        pos=pos^1;
        dp[0][pos]=2*dp[1][pos^1]%1000;        //A处的方案等于两边的方案相加，由于相等只算一边的*2
        dp[1][pos]=(dp[0][pos^1]+dp[2][pos^1])%1000;
        dp[2][pos]=(dp[1][pos^1]+dp[3][pos^1])%1000;
        dp[3][pos]=dp[2][pos^1];                     //D只能由C来
    }
    cout<<2*dp[3][pos]%1000<<endl;            //E由D和F来
    return 0;        
}

后续

接下来我会不断用C++来实现信奥比赛中的算法题、GESP考级编程题实现、白名单赛事考题实现，记录日常的编程生活、比赛心得，感兴趣的请关注，我后续将继续分享相关内容