div2
250pts MiddleCode
题意:s串长度为奇数时,将中间字符取掉并添加到t末尾;长度为偶数时,将中间两个较小的字符取掉并添加到末尾。
分析:直接做,学习了一下substr(s, pos, len)返回s中从pos开始的长度为len的字串。
500pts SplitIntoPairs
题意:将N个数(偶数)分成N/2组,使得两个数的乘积>=X的组数尽量多,X < 0。
分析:X < 0,所以只有当每组的两个数A,B一正一负时才有可能比X小,将N个数分成负数和非负数两组,如果负数有偶数个,那么结果就是N/2组,
因为负数,正数可以分别两两配对。当为奇数的时候,负数和正数两两配对正好剩下一个,且绝对值应该尽量小,判断两数之积和X的关系即可。
代码:
950pts GraphWalkWithProbabilities
题意:从一点出发,每一轮选择任意可达的点,该点有win[i], lose[i], 1-win[i]-lose[i]三个概率, 表示到达该点赢,输,继续的概率,从Start出发,
按照最优的走法,最后赢d的概率。
分析:从某一点x出发能够赢得概率和转移到相邻的点y,然后赢的概率有关,但是图中可能存在环,因此采用记忆化搜索的话,
会存在相互依赖关系构成环的情况,转移到一个点y要能够继续进行的话概率为-win[y]-lose[y],那么可以设从y出发,最多进行steps轮,最后能够赢得概率。
这样转移dp[node][steps] = max{ win[to] + (1-win[to]-lose[to]) * dp[to][steps-1] };
steps上界设为3000左右即可,因为1-win[to]-lose[to]最大0.99, 最多3000轮,最终赢得概率应该是能满足题目精度要求的。
代码:
div1
250pts MaxMinTreeGame
题意:给定一棵N(2 <= N <= 50)的树,两人轮流进行游戏,每次可以删除一条边,然后选择保留其中一棵子树,直到仅剩下一个结点,游戏结束,每个结点都有一个权值,
A想要使得 最后结果尽量大,B想要使得结果尽量小,两人均按照最优方式进行,A先手,求A最终得到的最大值。
分析:所有度数为1的点的中权值最大值(M)即为结果,首先要证明所能获得的最大值不会超过M,因为N>=2的树中度数为1 的结点至少2个,
所以不论A先手时如何操作,剩下的树中,一定会保留下这些结点中的一个,B操作时选取即可,然后证明A先手能够保留权值最大的结点,这个是显然的。
代码:
500pts PairsOfStrings
题意:给定字符集合为前k个小写字母,定义字符集合上的长度为n的A,B字符串,若存在定义在集合上的C使得A+C=C+B,那么(A,B)记为一对,
现在问(n,k)能够确定的数目,结果MOD (int)1e9 + 7。
分析:首先应该知道B应该是A旋转后的字符串,定义字符串的最小周期长度,A = d^n/d,表示A由n/d个长度为d字符串(记为s)链接构成,A = s + s + ... s,
且不存在更小的长度为d' < d的字符串s',s'重复n/d'之后能够得到A。这样A旋转操作能够得到的不同字符串就为d。那么对于本题需要知道最小周期长度的为d字符串有多少个(num),
最终结果就是所有的d*num之和。显然d应该是n的因子,可能的情况是k^d种,然后这里会有存在重复的情况,例如n = 8, d = 4时,结果k^4中,会包含d = 2中情况,
s = aaaa,A = s+s = aaaaaaaa,显然A可以看做周期长度更小的s' = aa,A = s' + s' + s' + s',所以要把d的因子d'所对应的情况排除。n <= (int)1e9,因子最多1300+个,最后复杂度应该是
O(1300*1300)。
代码:
1000pts SumOfArrays
题意:A,B两个数组长度 n <= 100000,A[i],B[i] < 100000,将A,B中的数排列后,使得C[i] = A[i]+B[i]使得C[i]中出现过的数Y出现次数最大。
分析:又是FFT的应用,做法很奇特!分别统计A[i]和B[i]中数出线次数即cntA[A[i]],cntB[B[i]],然后考虑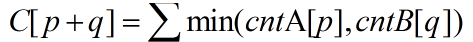
解法的关键之处就是这里的转化,考虑min(cntA[p],cntB[q]) >= k,那么C[p+q]为(p,q,k)的组数,针对k分别考虑:
k >= 10,显然cntA[p],cntB[q] >= k的p和去不超过(int)1e4,暴力统计C[p+q]的复杂度不会超过(int)1e8,当然实际复杂度可能更低。
k < 10,
z[] = full of zeros
For p = 0 ... 100000 {
For each q = 0 ... 100000 {
z[p + q] = z[p + q] + (x[p] * y[q])
}
}
for i = 0 ... 200000 {
C[i] = C[i] + z[i]
}
这里和大数的乘法十分相似,设立两个数组x[],y[],当x[p] = cntA[p] >= k,y[q] = cntB[q] >= k,剩下的部分利用FFT求出,z[p+q] += x[p]*y[q],由于FFT复杂度为O(MAX*log(MAX)),9次FFT是能够满足效率要求的。
250pts MiddleCode
题意:s串长度为奇数时,将中间字符取掉并添加到t末尾;长度为偶数时,将中间两个较小的字符取掉并添加到末尾。
分析:直接做,学习了一下substr(s, pos, len)返回s中从pos开始的长度为len的字串。
代码:
class MiddleCode {
public:
void Remove(string &s, int pos) {
int len = s.size();
string t = "";
if(pos < 0 || pos >= len) return;
for(int i = 0; i < len; i++)
if(i != pos) t += s[i];
s = t;
}
string encode(string s) {
int n = s.size(), m = n;
string ans = "";
for(int i = 0; i < n; i++) {
if((n-i)&1) {
ans += s[(n-i)/2];
Remove(s, (n-i)/2);
} else {
if(s[(n-i)/2] < s[(n-i)/2-1]) {
ans += s[(n-i)/2];
Remove(s, (n-i)/2);
} else {
ans += s[(n-i)/2-1];
Remove(s, (n-i)/2-1);
}
}
}
return ans;
}
};500pts SplitIntoPairs
题意:将N个数(偶数)分成N/2组,使得两个数的乘积>=X的组数尽量多,X < 0。
分析:X < 0,所以只有当每组的两个数A,B一正一负时才有可能比X小,将N个数分成负数和非负数两组,如果负数有偶数个,那么结果就是N/2组,
因为负数,正数可以分别两两配对。当为奇数的时候,负数和正数两两配对正好剩下一个,且绝对值应该尽量小,判断两数之积和X的关系即可。
代码:
class SplitIntoPairs {
public:
int makepairs(vector <int> A, int X) {
// int n = sz(A);
sort(A.begin(), A.end());
vector<int> B, C;
for(int i = 0; i < sz(A); i++){
if(A[i] >= 0) B.pb(A[i]);
else C.pb(A[i]);
}
int n = sz(B), m = sz(C);
if(n%2 == 0) return (n+m)/2;
return (n+m)/2-(1LL*C[m-1]*B[0] < X);
}
};950pts GraphWalkWithProbabilities
题意:从一点出发,每一轮选择任意可达的点,该点有win[i], lose[i], 1-win[i]-lose[i]三个概率, 表示到达该点赢,输,继续的概率,从Start出发,
按照最优的走法,最后赢d的概率。
分析:从某一点x出发能够赢得概率和转移到相邻的点y,然后赢的概率有关,但是图中可能存在环,因此采用记忆化搜索的话,
会存在相互依赖关系构成环的情况,转移到一个点y要能够继续进行的话概率为-win[y]-lose[y],那么可以设从y出发,最多进行steps轮,最后能够赢得概率。
这样转移dp[node][steps] = max{ win[to] + (1-win[to]-lose[to]) * dp[to][steps-1] };
steps上界设为3000左右即可,因为1-win[to]-lose[to]最大0.99, 最多3000轮,最终赢得概率应该是能满足题目精度要求的。
代码:
const int maxn = 3000 + 10;
double dp[55][maxn];
class GraphWalkWithProbabilities {
public:
vector<int> win, lose;
vector<int> g[55];
double dfs(int node, int steps) {
double &res = dp[node][steps];
if(!(res < 0)) return res;
res = 0;
for(int to: g[node])
res = max(res, win[to]/100.0 + (100-win[to]-lose[to])/100.0*dfs(to, steps-1));
return res;
}
double findprob(vector <string> graph, vector <int> winprob, vector <int> loseprob, int Start) {
for(int i = 0; i < 55; i++) for(int j = 0; j < maxn; j++)
dp[i][j] = -1.0;
// bug(1)
for(int i = 0; i < 55; i++) dp[i][0] = 0.0;
win = winprob;
lose = loseprob;
// bug(1)
int n = sz(graph);
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++)
if(graph[i][j] == '1')
g[i].pb(j);
}
dfs(Start, maxn-1);
return dp[Start][maxn-1];
}
};div1
250pts MaxMinTreeGame
题意:给定一棵N(2 <= N <= 50)的树,两人轮流进行游戏,每次可以删除一条边,然后选择保留其中一棵子树,直到仅剩下一个结点,游戏结束,每个结点都有一个权值,
A想要使得 最后结果尽量大,B想要使得结果尽量小,两人均按照最优方式进行,A先手,求A最终得到的最大值。
分析:所有度数为1的点的中权值最大值(M)即为结果,首先要证明所能获得的最大值不会超过M,因为N>=2的树中度数为1 的结点至少2个,
所以不论A先手时如何操作,剩下的树中,一定会保留下这些结点中的一个,B操作时选取即可,然后证明A先手能够保留权值最大的结点,这个是显然的。
代码:
const int maxn = 55;
int du[maxn];
class MaxMinTreeGame {
public:
int findend(vector <int> edges, vector <int> costs) {
memset(du, 0, sizeof du);
int n = sz(edges) + 1;
for(int i = 0; i < sz(edges); i++)
du[i+1]++, du[edges[i]]++;
int ans = 0;
for(int i = 0; i < n; i++)
if(du[i] == 1)
ans = max(ans, costs[i]);
return ans;
}
};500pts PairsOfStrings
题意:给定字符集合为前k个小写字母,定义字符集合上的长度为n的A,B字符串,若存在定义在集合上的C使得A+C=C+B,那么(A,B)记为一对,
现在问(n,k)能够确定的数目,结果MOD (int)1e9 + 7。
分析:首先应该知道B应该是A旋转后的字符串,定义字符串的最小周期长度,A = d^n/d,表示A由n/d个长度为d字符串(记为s)链接构成,A = s + s + ... s,
且不存在更小的长度为d' < d的字符串s',s'重复n/d'之后能够得到A。这样A旋转操作能够得到的不同字符串就为d。那么对于本题需要知道最小周期长度的为d字符串有多少个(num),
最终结果就是所有的d*num之和。显然d应该是n的因子,可能的情况是k^d种,然后这里会有存在重复的情况,例如n = 8, d = 4时,结果k^4中,会包含d = 2中情况,
s = aaaa,A = s+s = aaaaaaaa,显然A可以看做周期长度更小的s' = aa,A = s' + s' + s' + s',所以要把d的因子d'所对应的情况排除。n <= (int)1e9,因子最多1300+个,最后复杂度应该是
O(1300*1300)。
代码:
const int M = 1000000007;
class PairsOfStrings {
public:
int num[1500];
int powmod(LL a, LL b, LL c) {
LL res = 1;
while(b) {
if(b&1) res = res*a%c;
a = a*a%c;
b >>= 1;
}
return res;
}
void addIt(int &x, int y) {
x = (x+y)%M;
if(x < 0) x += M;
}
void getDivisors(int n, vector<int> &div) {
div.clear();
int m = (int)sqrt(n+.5);
for(int i = 1; i <= m; i++)
if(n%i == 0) {
div.pb(i);
if(n/i != i)
div.pb(n/i);
}
sort(div.begin(), div.end());
}
vector<int> div;
int getNumber(int n, int k) {
getDivisors(n, div);
int ans = 0;
for(int i = 0; i < sz(div); i++) {
int x = div[i];
num[i] = powmod(k, x, M);
for(int j = 0; j < i; j++) {
int y = div[j];
if(x%y == 0) {
addIt(num[i], -num[j]);
}
}
addIt(ans, 1LL*num[i]*x%M);
}
return ans;
}
};1000pts SumOfArrays
题意:A,B两个数组长度 n <= 100000,A[i],B[i] < 100000,将A,B中的数排列后,使得C[i] = A[i]+B[i]使得C[i]中出现过的数Y出现次数最大。
分析:又是FFT的应用,做法很奇特!分别统计A[i]和B[i]中数出线次数即cntA[A[i]],cntB[B[i]],然后考虑
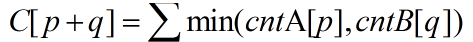
解法的关键之处就是这里的转化,考虑min(cntA[p],cntB[q]) >= k,那么C[p+q]为(p,q,k)的组数,针对k分别考虑:
k >= 10,显然cntA[p],cntB[q] >= k的p和去不超过(int)1e4,暴力统计C[p+q]的复杂度不会超过(int)1e8,当然实际复杂度可能更低。
k < 10,
z[] = full of zeros
For p = 0 ... 100000 {
For each q = 0 ... 100000 {
z[p + q] = z[p + q] + (x[p] * y[q])
}
}
for i = 0 ... 200000 {
C[i] = C[i] + z[i]
}
这里和大数的乘法十分相似,设立两个数组x[],y[],当x[p] = cntA[p] >= k,y[q] = cntB[q] >= k,剩下的部分利用FFT求出,z[p+q] += x[p]*y[q],由于FFT复杂度为O(MAX*log(MAX)),9次FFT是能够满足效率要求的。
代码:
const int maxn = (int)2e5 + 10;
const int LOW = 10;
int cntA[maxn], cntB[maxn];
int A[maxn], B[maxn], C[maxn];
bitset<maxn> a, b;
struct Complex {
double x, y;
Complex() {}
Complex(double x, double y):x(x), y(y) {}
};
Complex operator + (const Complex &a, const Complex &b) {
Complex c;
c.x = a.x+b.x;
c.y = a.y+b.y;
return c;
}
Complex operator - (const Complex &a, const Complex &b) {
Complex c;
c.x = a.x-b.x;
c.y = a.y-b.y;
return c;
}
Complex operator * (const Complex &a, const Complex &b) {
Complex c;
c.x = a.x*b.x-a.y*b.y;
c.y = a.x*b.y+a.y*b.x;
return c;
}
inline void FFT(vector<Complex> &a, bool inverse) {
int n = a.size();
for(int i = 0, j = 0; i < n; i++) {
if(j > i)
swap(a[i], a[j]);
int k = n;
while(j & (k>>=1)) j &= ~k;
j |= k;
}
double PI = inverse ? -pi : pi;
for(int step = 2; step <= n; step <<= 1) {
double alpha = 2*PI/step;
Complex wn(cos(alpha), sin(alpha));
for(int k = 0; k < n; k += step) {
Complex w(1, 0);
for(int Ek = k; Ek < k+step/2; Ek++) {
int Ok = Ek + step/2;
Complex u = a[Ek];
Complex t = a[Ok]*w;
a[Ok] = u-t;
a[Ek] = u+t;
w = w*wn;
}
}
}
if(inverse)
for(int i = 0; i < n; i++)
a[i].x = (a[i].x/n);
}
vector<int> operator * (const bitset<maxn> &v1, const bitset<maxn> &v2) {
int S1 = v1.size(), S2 = v2.size();
int S = 2;
while(S < S1+S2) S <<= 1;
vector<Complex> a(S), b(S);
for(int i = 0; i < S; i++)
a[i].x = a[i].y = b[i].x = b[i].y = 0.0;
for(int i = 0; i < S1; i++)
a[i].x = v1[i];
for(int i = 0; i < S2; i++)
b[i].x = v2[i];
FFT(a, false);
FFT(b, false);
for(int i = 0; i < S; i++)
a[i] = a[i] * b[i];
FFT(a, true);
vector<int> res(maxn, 0);
for(int i = 0; i < maxn; i++)
res[i] = round(a[i].x);
return res;
}
class SumOfArrays {
public:
void gen(int A[], vector<int> seed, int n) {
A[0] = seed[0];
A[1] = seed[1];
for(int i = 2; i < n; i++)
A[i] = (1LL * A[i-1] * seed[2] + 1LL* A[i-2] * seed[3] + seed[4]) % seed[5];
// for(int i = 0; i < n; i++)
// printf("%d ", A[i]);
// puts("");
}
char ans[100];
string findbestpair(int n, vector <int> Aseed, vector <int> Bseed) {
gen(A, Aseed, n);
gen(B, Bseed, n);
// memset(cntA, 0, sizeof cntA);
memset(cntB, 0, sizeof cntB);
memset(C, 0, sizeof C);
for(int i = 0; i < n; i++) {
cntA[A[i]]++;
cntB[B[i]]++;
}
vector<int> bigA, bigB;
for(int i = 0; i < maxn; i++) {
if(cntA[i] >= LOW)
bigA.pb(i);
if(cntB[i] >= LOW)
bigB.pb(i);
}
for(int p: bigA) for(int q: bigB) {
C[p+q] += min(cntA[p], cntB[q]) - LOW + 1;
}
vector<int> c(maxn);
for(int k = 1; k < 10; k++) {
a.reset();
b.reset();
for(int i = 0; i < maxn; i++) {
if(cntA[i] >= k)
a[i] = 1;
if(cntB[i] >= k)
b[i] = 1;
}
c = a*b;
for(int i = 0; i < maxn; i++)
C[i] += c[i];
// for(int i = 1; i <= 4; i++)
// cout << C[i] << ' ';
// cout << endl;
}
int X = -1, Y = 0;
for(int i = 0; i < maxn; i++)
if(C[i] >= X) {
X = C[i];
Y = i;
}
sprintf(ans, "%d %d", X, Y);
// TL
return ans;
}
};





















 468
468

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








