“最小表示法”思想在字符串循环同构问题中的应用(摘自周源的ppt)
前言:
“最小表示法”比起动态规划、贪心等思想,在当今竞赛中似乎并不是很常见。但是在解决判断“同构”一类问题中却起着重要的作用。
本文即将讨论字符串中的同构问题,如何巧妙地运用最小表示法来解题呢,让我们继续一起思考吧。
到底什么是循环同构的字符串呢?
直接举个例子:
比如 str1 = "abdea" 而字符串str2是str1从第i(i>0)个开始将str1从i循环到末尾再从头开始循环到i,那么这两个字符串就是循环同构的.比如str2 = "deaab";
那么什么是字符串的最小表示呢?
比如上面那个str1,就是从str1的同构字符串中字典序最小的,那么str1的最小表示就是"aabde".
如何得到一个字符串的最小表示?
设函数M(s)返回值意义为:
从s的第M(s)个字符引起的s的一个循环表示是s的最小表示。
若有多个值,则返回最小的一个
比如M("bbbaab") = 4; 也就是最小表示为aabbbb,是从字符串"bbbaab"的第4个的字符开始的同构字符串。
现在换一种思路:
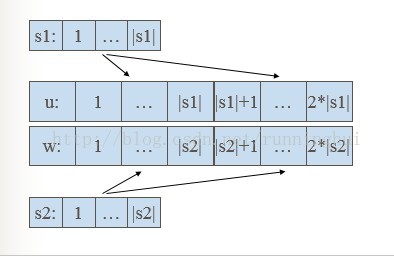
设有字符串s1,s2
设u=s1+s1(也就是将s1复制一份到s1后面),w=s2+s2并设指针i,j指向u,w第一个字符
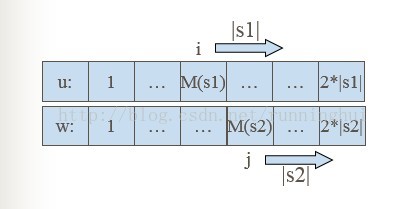
如果s1和s2是循环同构的,那么当i,j分别指向M(s1),M(s2)时,一定可以得到u[i→i+|s1|-1]=w[j→j+|s2|-1],迅速输出正确解。
同样s1和s2循环同构时,当i,j分别满足
i≤M(s1),j≤M(s2)时,
两指针仍有机会达到i=M(s1),j=M(s2)这个状态。
问题转化成,两指针分别向后滑动比较,如果比较失败,如何正确的滑动指针,新指针i’,j’仍然满足
i’≤M(s1),j’≤M(s2)
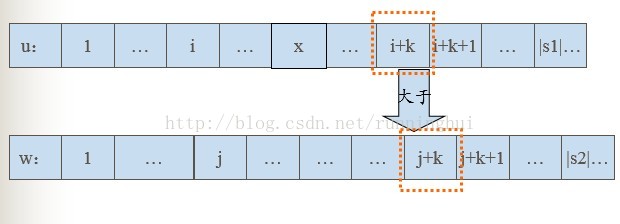
设指针i,j分别向后滑动k个位置后比较失败(k≥0),即有
u[i+k]≠w[j+k]
设u[i+k]>w[j+k],同理可以讨论u[i+k]<w[j+k]的情况。
因为u[x]在u[i]后(x-i)个位置,
对应的可以找到在w[j]后(x-i)个位置的w[j+(x-i)],
同样对应的有u[x+1]和w[j+(x+1-i)],u[x+2]和w[j+(x+2)-i],
直到u[i+k-1]和w[j+k-1]。
它们都是相等的,
即有u[x→i+k-1]=w[j+(x-i)→j+k-1]。
很容易就得到u[x→i+k]>w[j+(x-i)→j+k]。
所以s1(x-1)不可能是s1的最小表示!
因此M(s1)>i+k,
指针i滑到u[i+k+1]处仍可以保证小于等于M(s1)!

同理,当u[i+k]<w[j+k]的时候,可以将指针j滑到w[j+k+1]处!
也就是说,两指针向后滑动比较失败以后,
指向较大字符的指针向后滑动k+1个位置。
举例:
设s1=‘babba’,s2=‘bbaba’。(两个同构字符串)
u=s1+s1='babbababba' w=s2+s2='bbababbaba'
初始化i=0,j=0,k=0;(i作为u的指针,j作为w的指针)
比较失败时k=1 (u[i+k]!=w[j+k]
由于u[i+k]<w[j+k] 所以j=j+k+1;
j = 2 i不变(i=0); k=0
继续比较发现当k=0时u[i+k]>w[j+k],所以i=i+k+1;
i=1,j不变(j=2);k=0;
继续比较,发现当k=2时u[i+k]>w[j+k]所以i = i+k+1;
i = 4j不变(j=2)k=0;
继续比较,这个时候就找到了最小表示ababb
下面贴下模板
int getminsub(char *a)
{
int i=0,j=1,len=strlen(a),k=0; //取两个同构的字符串一个从下标0开始,一个从下标1开始
while(i<len&&j<len&&k<len) //这里并没有将字符串复制一份添加到后面
{
if(k==len) break; //说明找到了a的最小表示
if(i==j) j++;
int ni=i+k,nj = j+k;
if(ni>=len) ni-=len; //就是回到字符串的开始去
if(nj>=len) nj-=len;
if(a[ni]>a[nj])
{
i+=k+1;
k=0;
}
else if(a[ni]<a[nj])
{
j+=k+1;
k=0;
}
else k++;
}
return i; //返回从第i个字符开始时a的最小表示
}






















 1202
1202

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








