非线性方程组求解迭代算法&图像寻初始值讲解

前段时间过冷水在学习中遇到了一个解非线性方程组的问题，遇到非线性方程组的的问题过冷水果断一如既往、毫不犹豫的 fsolve()、feval()函数走起，直到有人问我溯本求源的问题——非线性方程组求解算法。

于是过冷水就去查了一下解非线性方程组的算法，觉得Newton-Raphson method算法针对我们的问题比较合适，本期过冷水就给大家讲讲该算法思路

已知方程f(x)=0有近似根x_k将函数f(x)在x_k展开，可得：

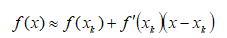
于是方程f(x)=0可以近似表示为:

这是个线性方程，记其根为x_k+1,则x_k+1的计算公式为：

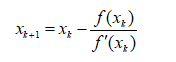
这就是解一元非线性方程的牛顿迭代法公式，我们的问题是非线性方程组，需要把一元扩展到二元。

记非线性方程组为：F(B₁₂,B₂₁)=0,函数F(B₁₂,B₂₁)的导数F^、(B₁₂,B₂₁)称为雅克比矩阵，表示为：

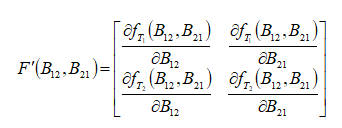
非线性方程组的牛顿迭代法就是直接将单方程的牛顿迭代法的套用；

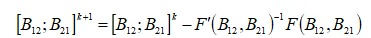
该算法就是如此的简单，来让我们看一下具体编程实现过程：

clear all
warning off
feature jit off
%%绘制方程组显式
syms B12 B21
f1=exp((100*B21)/6363 - (993408755695616*exp(-(20*B12)/6363))/23832915087626075 - log((23832915087626075*exp(-(20*B21)/6363))/993408755695616) + (100*B12*exp(-(20*B12)/6363))/6363 + 1) - 449/100;
f2=exp((100*B21)/6563 - log((95989234274612025*exp(-(20*B21)/6563))/3973635022782464) - (3973635022782464*exp(-(20*B12)/6563))/95989234274612025 + (100*B12*exp(-(20*B12)/6563))/6563 + 1) - 201/50;
F=[f1;f2];
Y=latex(F)
str=['$',Y,'$']
figure1 = figure('Color',[1 1 1]);
axes1 = axes('Parent',figure1,'Position',[0.13 0.11 0.8 0.8]);
axis off
hold(axes1,'on');
text('Parent',axes1,'FontSize',30,'FontName','Times New Roman','Interpreter','latex','String',str,'Position',[-0.0829467939972715 0.339583333333333 0],'Visible','on');
set(axes1,'FontName','Times New Roman','FontSize',14,'FontWeight','bold');


%%牛顿迭代法求方程组的根
syms B12 B21
f1=exp((100*B21)/6363 - (993408755695616*exp(-(20*B12)/6363))/23832915087626075 - log((23832915087626075*exp(-(20*B21)/6363))/993408755695616) + (100*B12*exp(-(20*B12)/6363))/6363 + 1) - 449/100;
f2=exp((100*B21)/6563 - log((95989234274612025*exp(-(20*B21)/6563))/3973635022782464) - (3973635022782464*exp(-(20*B12)/6563))/95989234274612025 + (100*B12*exp(-(20*B12)/6563))/6563 + 1) - 201/50;
F=[f1;f2];
dF = jacobian(F);
x=[100;100];
[B12 B21 ]=deal(x(1),x(2));
 F=subs(F);
dF=subs(dF);%赋予其初始值为了第一步的判断误差
B12=50;B21=50;
x=[150;110];
while abs(x-[B12;B21])>0.0001 
    %% a 为方程组公式的具体展开形式；b为雅克比矩阵的具体展开形式
    B12=x(1);B21=x(2);
    a=[eval(char(f1));eval(char(f2))];
    b=[eval(char(dF(1,1))),eval(char(dF(1,2)));eval(char(dF(2,1))),eval(char(dF(2,2)))]
    F=subs(a);
    dF=subs(b);
    x=x-inv(double(dF))*double(F);
end

在牛顿迭代法过程中中要赋予迭代初始值，对优化算法有了解的读者就知道初始值对优化算法影响是很大的，针对上述特定问题过冷水就想出了一种特殊判断初始值的方法。

复杂的非线性方程组往往会存在多解的情况，用算法或者matlab自带函数很难一次性求出全部解，都是给出初始值附近的解（局部解），过冷水就行如果能够用三维图绘制出线性方程组的解区间示意图该多好。于是就尝试用三维图解决我的问题。x轴为B₁₂,y轴为B21,Z轴是f(g21,g21,T)，在f(g21,g21,T)这个曲面上找出满足所有f(g21,g21,T1)=0的[g21,g21] 可知其为一条线。用等高线1表示。然后再找出满足所有f(g21,g21,T1)=0的[g21,g21]，可知其为另外一条等高线2线。两条两条线的交点就是该方程组的解。如图。

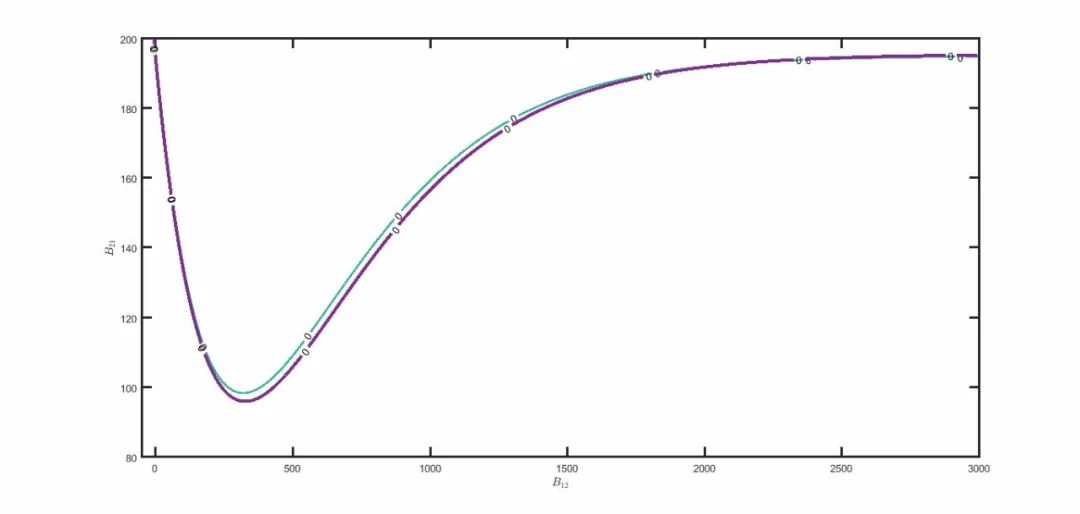
图像代码如下：