阶乘 (牛客小白月赛23)

题目传送门

题目描述

给定一个正整数 p
求一个最小的正整数 n，使得 n! 是 p 的倍数

输入描述:
第一行输入一个正整数T表示测试数据组数
接下来T行，每行一个正整数p

输出描述:

输出T行，对于每组测试数据输出满足条件的最小的n。

示例1
输入

4
1
2
4
8

输出

1
2
4
4

题解：这道题说的很明白，这里用二分法进行求解，这里我们把p分解成质因子的幂相乘的形式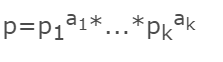
，因此我们只要找出一个数满足所有p中每个质因子出现的次数小于这个数用唯一分解定理分解之后，每个质因子出现的次数即可。因为我们要求的数是阶乘的形式，所以在计算质因子出现的个数的时候要这样计算，举个例子假如要计算8的阶乘中 2这个因子分解的次数，这里我们就这样理算，因为8的阶乘里面能整除2的数有 2 4 6 8，四个，除以2之后1-4之内是2的倍数的数有2 4两个，再除2之后1-2之内2的倍数的数有1个，所以这里一共有4+2+1=7个，

bool check(int x)//判断这个数是否满足条件
{
   
    for(int i=1;i<=k;i++)//k是p的所有质因子数
    {
      int primernum=0,n=x;//primernum是判断的这个数，有几个prime[i]这个质因子数
      while(n)
      {
      primernum+=n/prime[i];//计算阶乘中有几个此时的质因子
        n/=prime[i];
      }
      if(primernum<num[i])return false;//如果某个质因子在x中的分解出来的次数小于在p中出现的次数，那么说明不符合条件
    }
    return true;//执行到这一步表示符合条件
}

下面是唯一分解定理求出p的所有质因子，并求出每个质因子出现的次数。

for(int i=2;i*i<=p;i++)
  {
      if(p%i==0)
      {
          prime[++k]=i;
          while(p%i==0)
          {
            num[k]++;
            p/=i;
          }
      }
  }
  if(p>1) prime[++k]=p,num[k]++;

这个时候我们已经把p用埃氏筛进行分解，每个质因子的个数也都已经求出来了，这个时候我们只需要对x就行二分即可，取l=1，r=1e9;如果mid符合条件那么我们就舍弃左边部分，因为是阶乘，如果mid不符合条件，那么1-mid也都是不符合，因此舍弃左边部分，然后一直维护ans的值即可。

下面是AC代码

#include<bits/stdc++.h>
using namespace std;
const int inf=0x3f3f3f3f;
const int maxn=1e6+100;
int prime[maxn],num[maxn];
int k,t,p;
bool check(int x)
{
   
    for(int i=1;i<=k;i++)
    {
      int primernum=0,n=x;
      while(n)
      {
      primernum+=n/prime[i];
        n/=prime[i];
      }
      if(primernum<num[i])return false;
    }
    return true;
}
void solve()
{
    k=0;
  for(int i=2;i*i<=p;i++)
  {
      if(p%i==0)
      {
          prime[++k]=i;
          while(p%i==0)
          {
            num[k]++;
            p/=i;
          }
      }
  }
  if(p>1) prime[++k]=p,num[k]++;
  int l=1,r=1e9,mid,ans;
  while(l<=r)
  {
      mid=(l+r)/2;
      if(check(mid))r=mid-1,ans=mid;
      else l=mid+1;
  }
  memset(prime,0,sizeof prime);
  memset(num,0,sizeof num);
  cout<<ans<<endl;
}
int main()
{
   
    cin>>t;
    while(t--)
    {
      cin>>p;
      solve();
    }
    system("pause");
}

写的很仓促，有错误请联系我。